平均50.5点(前年比;+7.9点)
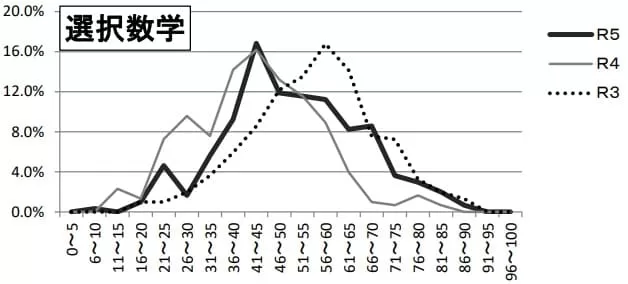
問題はこちら→埼玉県総合教育センター
大問1(小問集合)
(1) 75.2%
10xy2×(-2/3xy)2÷(-5y2)
=10xy2×4/9x2y2÷(-5y2)
=-8/9x3y2
(2) 75.2%
恒例の対称式。
xy=(3+√7)(3-√7)=9-7=2
x+y=(3+√7)+(3-√7)=6
x-y=(3+√7)-(3-√7)=2√7
x3y-xy3
=xy(x2-y2)
=xy(x+y)(x-y) ←ここで代入
=2×6×2√7
=24√7
(3) 84.8%(一部正答0.3%)
(5x-2)2-2(5x-2)-3=0 ←(5x-2)=Xに置き換える
X2-2X-3
=(X-3)(X+1)
=(5x-2-3)(5x-2+1) ←戻す
=(5x-5)(5x-1)
=5(x-1)(5x-1)=0
x=1/5、1
(4) 92.1%
共通問題と同様。
全数調査は調査対象すべてを調べ上げる。
標本調査は母集団のなかから標本を無作為に抽出して、母集団の様子を推し量る。
総務省統計局が5年に1度行う国勢調査は全数調査の代表例。
国の基礎的な統計資料として国策の判断に使われる。
健康診断も個々人のデータをとらなければ意味がないので全数調査。
河川の水質調査とテレビの視聴率は一部を調べる標本調査。
ア・ウ
@テレビの視聴率@
標本(サンプル)の大きさはどの程度求められるか。
大学レベルの統計学の知識が求められると思うのでサボにはわかりませんが、
視聴率を計測する機器が設置されているテレビの台数は、
全体の0.01%にも満たないようですw( ゚Д゚)w
視聴率調査に協力している人を全く見掛けない理由(ねとらぼ)
↑この記事によると、2017年10月時点で調査対象世帯は全体の0.00005%以下となっている…。
それだけで残りの99.999…%以上を推し量って良いものなのか疑問に思われますが、
統計学的には十分信頼するに足りるサンプル数なんだとか。
どうやら母集団が大きくなるほど、標本の大きさは思ったより小さくても間に合うようです。
反対に母集団が小さいと(例えば1つのクラスの動向では)多くの標本をとらなければならない。
(5) 83.8%
共通問題と同様。
3枚の硬貨を投げた結果は、23=8通り
100円玉が表になれば100円以上になるので、余事象で考えてみる。
100円未満は〔3枚すべて裏〕〔2枚の50円玉のうち1枚が裏〕の3通り。
100円以上は5通りで、確率は5/8。
(6) 36.6%
共通問題と違い、図が与えられていない。
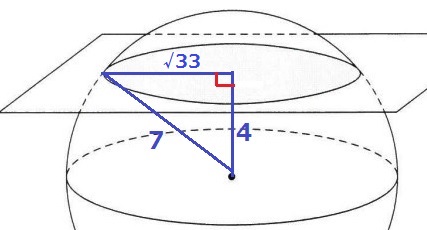
断面の円の半径は、三平方から√(72-42)=√33cm
断面の円の面積は、√33×√33×π=33πcm2
*誤答は9πが多かった。
(7) 48.2%(一部正答20.1%)
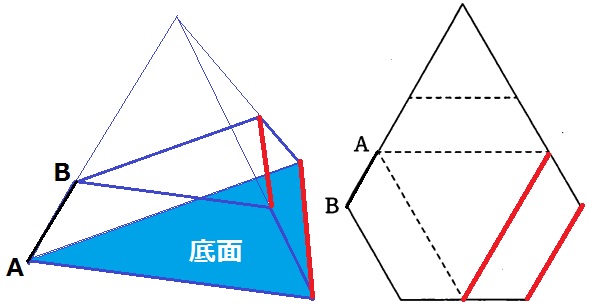
正四面体を横に切った立体になる。
頂点…6個、辺…9本、ABとねじれの位置にある辺…赤線の2本
(*延長して交わったらネジレではない!)
@オイラーの多面体定理@
【頂点の数-辺の数+面の数=2】
ドーナツのような穴のある多面体でなければ、どんな多面体でも成り立つ定理です。
本問の立体であれば、6-9+5=2
(8) 73.3%
Xの百の位をa、一の位をbとする。
X=100a+70+b
Y=100b+70+a
X-Y
=(100a+70+b)-(100b+70+a)
=99a-99b
=99(a-b)=396
a-b=4 …①
仮定より、a+b=15-7=8 …②
①、②の連立を解くと、a=6、b=2
672
(9) 44.9%(一部正答2.3%)
y=2x2はa>0だから下に凸のグラフ。
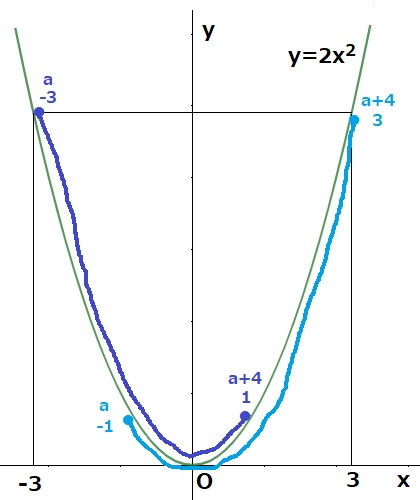
yの最小値0から、原点は必ず通過する。
yの最大値18を式に代入して、18=2x2
x=3か-3に触れなくてはならない。
a≦x≦a+4→x座標の差が4
条件を満たすaは上図より、a=-1、-3
(10) 38.6%(部分正答9.2%)

18人のQ2(第2四分位数;中央値)は9番目と10番目の平均。
30~40分、40~50分いずれかの階級に含まれる。
Q1(第1四分位数)は下位9人の真ん中、下から5番目。
Q3(第3四分位数)は上位9人の真ん中、上から5番目。
ヒストグラムと箱ひげ図で値が明確に異なるのはQ3。
ヒストグラムのQ3は40分以上50分未満の階級に含まれるが、
箱ひげ図のQ3は50分以上の60分未満の階級に含まれる。
大問2(作図・証明)
(1) 26.4%!(一部正答35.0%)
∠BPA=15×2=30°となる回転の中心Pを作図する。
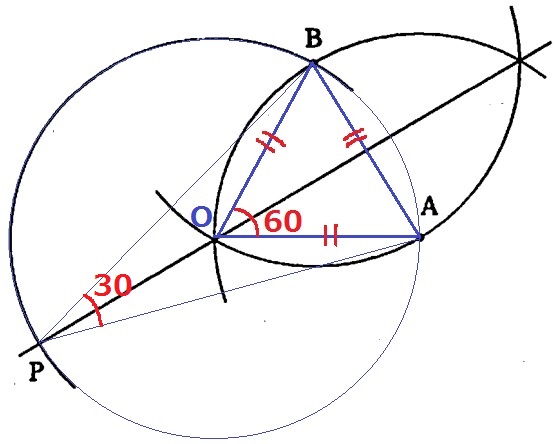
AとBは円周上の2点。
Aが反時計回りに回転移動した点がBだから、
回転の中心PはABの垂直二等分線上の左側にある。
ABの長さをとり、AとBそれぞれから弧を描く。
左側の交点をOとすると、△OABは3辺が等しい正三角形。
∠BOA=60°
円周角は中心角の半分だから、∠BPA=60÷2=30°
Oを中心に円弧を描き、Bの反対側の交点がPである。
(2) 23.4%!(一部正答66.0%)
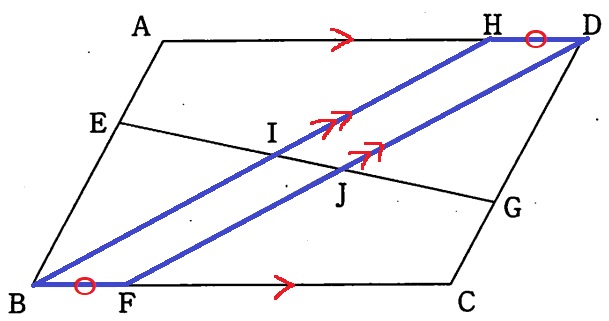
まず、等角の指摘に必要なBH//FDを証明しておく。
四角形DHBFはHD//BF、HD=BFより、
1組の対辺が平行で、かつ長さが等しいから平行四辺形→BH//FD
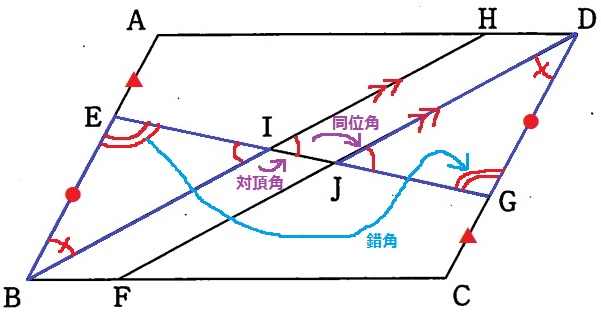
平行四辺形の対辺は等しい。AB=CD
仮定からAE=CG(▲)なので、BE=DG(●)がいえる。
錯角で、∠BEI=∠DGJ
対頂角と同位角より、∠EIB=∠GIH=∠GJD
残りの角から、∠EBI=∠GDJ
1辺両端角が等しいので合同。
大問3(規則)
(1) 72.9%(一部正答16.8%)
共通問題と同様。
●偶数の中では唯一、n=6のときだけ0.16666…と無限小数が起きている。
●1桁の奇数ではn=5が有限小数だった。2桁の奇数において5の倍数に絞って考える。
問題文では20と32のあいだにイがあり、この範囲にある5の倍数の奇数は25しかない。
1/25=4/100=0.04(←有限小数)
ア…6、イ…25
(2) 52.1%(一部正答11.9%)
1÷7=0.1428571428…
〔142857〕がループする。
この6個の数を1周とすると、30÷6=5
30番目は5周目の終わりの7。
1周の和は、1+4+2+8+5+7=27
5周の和は、27×5=135
小数第30位の数…7、和…135
大問4(関数)
(1) 84.8%
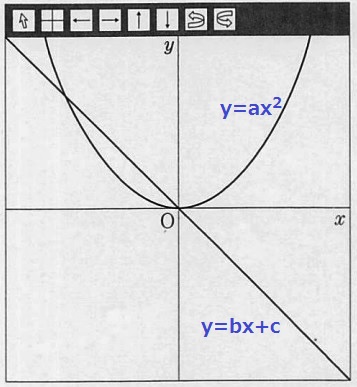
y=ax2は下に凸のグラフ。a>0
y=bx+cは右下なので傾きb<0、切片c=0
b<c<a(a>c>b)
(2)① 15.5%!(一部正答46.2%)
答案では説明も記述する。
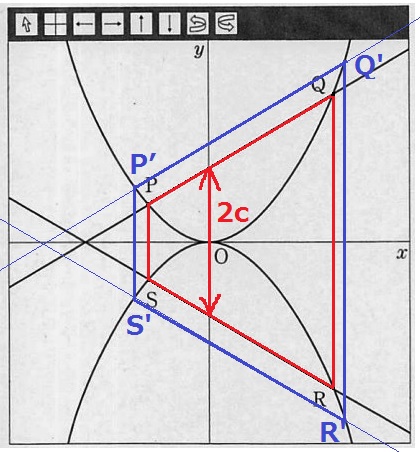
台形PSRQはx軸について上下対称。
切片cの値を大きくすると、台形の上底PS、下底QR、高さが長くなり、
台形PSRQの面積は2乗に比例する形で大きくなる。
ア
*イを選択する誤答が多かった。
② 3.6%!!(一部正答7.3%)

各点の座標を文字で表す。
y=ax2にx=-1、2を代入して、P(-1、a)Q(2、4a)
Sはx軸に関してPと対称だから、S(-1、-a)
PQの傾きはPから右に3、上に3aだから、3a÷3=a
これはy=bx+cの傾きbに相当するので、a=b
SQの傾きはSから右に3、上に5aだから、5/3a=1
a=b=3/5
y=3/5x+cにP(-1、3/5)を代入して、
3/5=3/5×(-1)+c
c=6/5
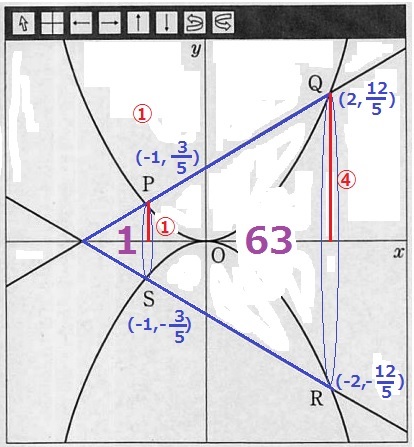
小さい円錐と大きい円錐の相似比は①:④
体積比は相似比の3乗。
小さい円錐の体積を①3=1とすると、大きい円錐の体積は④3=64
回転体の円錐台の体積は、小さい円錐を63倍すればいい。
3/5×3/5×π×1÷3×63=189/25πcm3
a=3/5、b=3/5、c=6/5、体積…189/25πcm3
大問5(空間図形)
(1) 53.1%
共通問題と同様。

最短距離なので、展開図を作成。
△IEG∽△PFGより、PF=2×4/8=1cm
BP=6-1=5cm
Pは秒速1cmだから5秒後。
*誤答は4秒後が多かった。
(2) 4.6%!!(一部正答8.6%)
答案では途中の説明も書かなくてはならない(´゚д゚`)
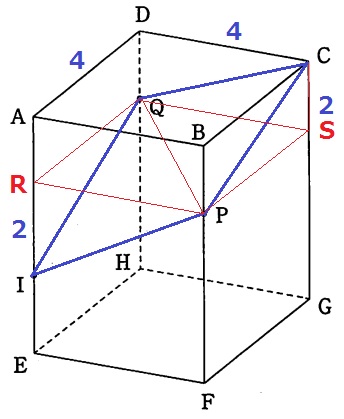
断面を正確に捉える。
Iから2cm上がってP・Q。さらに2cm上がって断面はCを通過する。
P、Qを通る面ABCDに平行な面とAIの交点をR、CGとの交点をSとする。
三角錐I―PQRと三角錐C―PQSにおいて、
底面の△PQRと△PQSは正方形を2つに割った直角二等辺で合同。
高さはIR=CS=2cmだから、2つの三角錐は体積が等しい。
平均の発想で三角錐I―PQRを三角錐C―PQSに移動させると、
求積すべき立体は直方体になる。
4×4×2=32cm3
(3) 0.3%!!!

接点あたりを分析したいので、△IPQが直線にみえる面AEGCで切り取る。
球の中心をO、接点をTとする。
半径と接線は直交するので、OT⊥IP
BPが知りたいが求めづらい。
OF=2cmなので、POの長さを出せないか。
△PTOに関する情報が欲しい。

IとOが同じ高さにある点に注目する。
IOの長さは、直角二等辺EFGの斜辺EGの半分。
IO=4√2÷2=2√2cm

直角三角形TIOにおいて、TO=2cm、IO=2√2cmということは、
三平方の定理から、辺の比が1:1:√2の直角二等辺三角形。
45°を記していくと、△PTOも△PIOも直角二等辺である。
PO=IO=2√2cm
x=BF-PF=6-(2√2+2)=4-2√2
●講評●
大問1
(2)来年も対称式は出る(はず)。
(3)最後は共通因数5を外に出す。
(6)図がなくてもイメージできるようにしたい。
(9)差がつきそう。
グラフ上でxの変域が4の曲線を移動させて、原点と±3が触れる場所を探す。
(10)第3四分位数の違いは見えやすかった。
大問2
(1)PはABから左に離れている場所にある。
中心角60°の作成→円周角30°の流れでPの位置を探す。
(2)類題をどこかで見かけた。
大問3
(2)中学受験では典型題に入るので、学校選択者は解けるようにしておきたい。
大問4
(2)①大きくなるのはイメージしやすいが、記述がやや独特。
台形のどこか伸びたことで面積が大きくなるか。
②1つ1つの作業を丁寧に行いたい。
大問5
(2)この手のタイプでも記述が要求された。
形を変えられるということは、P・Qより上の部分と下の部分が等積。
三角錐の合同を指摘すればいい。
(3)接線と半径が直交する様子を描けるのはどの面か。
IとOの高さが突破口になる。



コメント