2020年度　愛媛県公立高校入試問題過去問【数学】解説

平均26.1点（前年比；＋1.1点）
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
－５＋２＝－３

（２）
３（４ａ－３ｂ）－６（ａ－１/３ｂ）
＝12ａ－９ｂ－６ａ＋２ｂ
＝６ａ－７ｂ

（３）
４ｘ²ｙ×３ｙ÷６ｘ²
＝２ｙ²

（４）
（２√５＋１）（２√５－１）＋√12/√３　←うしろの項は根号の中を約分
＝（２√５）²－１²＋√４
＝20－１＋２＝21

（５）
（ｘ－４）（ｘ－３）－（ｘ＋２）²
＝ｘ²－７ｘ＋12－ｘ²－４ｘ－４
＝－11ｘ＋８

大問２（小問集合）

（１）
－12/ａ－ｂ²
＝－12/２－（－３）²
＝－６－９
＝－15

（２）
ｘ²＋２ｘ－35
＝（ｘ＋７）（ｘ－５）＝０
ｘ＝－７、５

（３）
反比例はｙ＝ａ/ｘ
比例定数ａ＝－６を代入。
式；ｙ＝－６/ｘ

反比例なので双曲線を描く。
ｘとｙの積は－６で一定。
ａ＜０だから、第２象限と第４象限となる。

（４）①
愛媛だからミカンの糖度が題材に。
ア＝40－（２＋13＋12＋９）＝４

②
糖度11～13度は40個中25個の割合。
8000×25/40＝5000個

（５）
６枚から２枚を選ぶ→₆Ｃ₂＝15通り

負の数の－３か－２をとると、和が正にならない可能性がでてくる。
そこで、和が負か０になる場合を求めて全体から引く。
◆－３をひく
もう１枚は何をとっても負か０になる→５通り。
◆－２をひく
もう１枚は０～２→３通り。（－３は先ほどカウント済み）
以上８通り。

和が正になる場合は15－８＝７通り
確率は７/15。

（６）

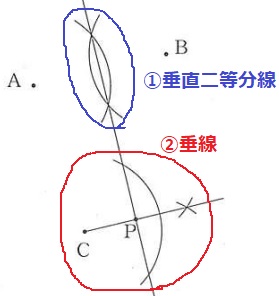
『２点Ａ、Ｂから等しい距離にある』→ＡＢの垂直二等分線
『Ｃから最も近いＰ』→Ｃを通る垂線、交点がＰとなる。

（７）
解答では過程も記述する。
まずは邪魔な赤ピーマンを除外。
大根とレタスの重さの合計は、175－50＝125ｇ

カロリーは１ｇあたりに直すこと！
赤ピーマンは１ｇあたり0.3kcalなので、
大根とレタスの熱量の合計は、33－0.3×50＝18kcal

大根をｘｇ、レタスをｙｇとすると、
ｘ＋ｙ＝125
0.18ｘ＋0.12ｙ＝18
これを解いて、ｘ＝50、ｙ＝75
大根…50ｇ、レタス…75ｇ

大問３（文字式）

（１）
扇形は円の一部。中心角の処理は時間で考えよう。
円を１周するのに16分。
４分間乗るので、20×２×π×４/16＝10πｍ

（２）①
今度はゴンドラの台数で考える。
１周24台で16分かかる。
８台では、16分×８/24＝16/３分後

②

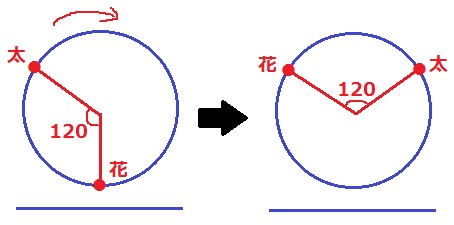
24台のうちの８台だから、太郎と花子は円の１/３離れている。中心角は120度。
この位置関係で時計回りに回ると、右図で高さが等しくなる。

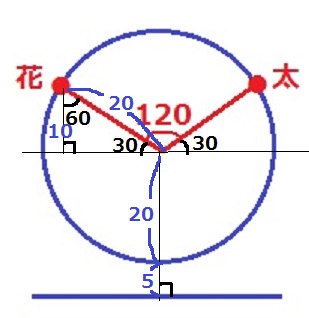
円の中心を通る、地面に平行な直線を引く。
左右対称の図形だから、（180－120）÷２＝30°
内角が30°－60°－90°の直角三角形は辺の比が１：２：√３
→直角三角形の高さは10ｍ。
10＋20＋５＝35ｍ

（３）
発想力がとわれる。
これもゴンドラの台数で考える。

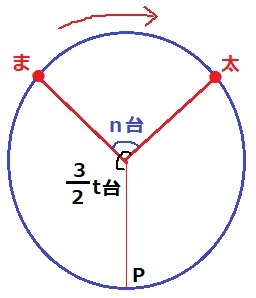
太郎とまことのあいだがｎ台。
観覧車１周は16分で24台まわる。
ｔ分後のゴンドラの台数は、24台×ｔ/16＝３/２ｔ台
この３/２ｔ台は、まことと太郎が同じ高さになったときのＰ～太郎までの台数。

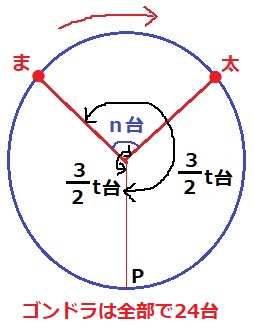
対称性から、反時計回りにＰからまことまでの台数も３/２ｔ台。
３/２ｔ＋３/２ｔ－ｎ＝24
３ｔ＝ｎ＋24
ｔ＝１/３ｔ＋８

大問４（数量変化）

（１）

図に書き込んでみよう。
■ｘ＝１のとき
ｙ＝２×１÷２＝１

■ｘ＝４のとき
ｙ＝６×４÷２＝12

（２）
正方形ＡＢＣＤの周の長さは24ｃｍ。
言い換えれば、ＰとＱは24ｃｍ離れた状態から毎秒３ｃｍずつ近づいていく。
24÷３＝８秒後

（３）
変化するポイントごとに調べる。

０～３秒は底辺と高さがともに伸びる。△ＡＰＱは放物線で増加。
３～６秒はＡＱを底辺とすると底辺のみ毎秒１ｃｍずつ伸びる。
高さは６ｃｍで変化なし。面積は比例で増加。
６～８秒はＰＱを底辺とすると底辺が毎秒３ｃｍずつ縮む。
高さは６ｃｍで変化なし。面積は比例で減少（３～６秒の傾きの－３倍）。
ウ

（４）

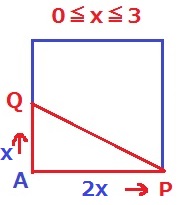
３秒後の△ＡＰＱの面積は６×３÷２＝９ｃｍ³だから、３秒より前に１つある。
ＡＱ＝ｘとすると、ＡＰ＝２ｘ
２ｘ×ｘ÷２＝６
２ｘ²＝12
ｘ＞０より、ｘ＝√６

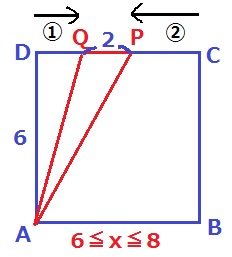
ＱＰ＝２ｃｍになれば、△ＡＰＱの面積は６ｃｍ²となる。
ＰとＱの速さの比から、ＤＱ：ＰＣ＝①：②
ＤＱ＝（６－２）×①/③＝４/３ｃｍ
Ｑの移動距離は、６＋４/３＝22/３ｃｍ
Ｑは毎秒１ｃｍなので、22/３秒後。
ｘ＝√６、22/３

大問５（平面図形）

（１）①
『△ＡＦＣと△ＢＥＣ』とあるので、もしこれらが合同であった場合、
ＡＦに対応する辺を選べばいい。
ＢＥ
*うしろの証明を終わった後に戻ってきても可。

②
△ＡＦＣ≡△ＢＥＣの証明。

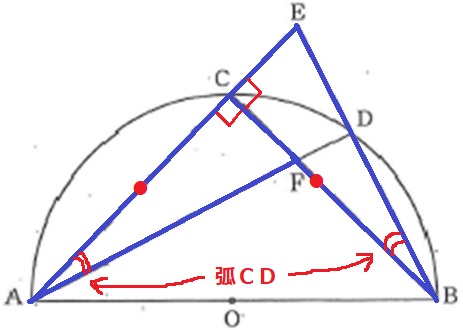
仮定からＡＣ＝ＢＣ
弧ＣＤに対する円周角で∠ＣＡＦ＝∠ＣＢＥ
直径に対する円周角から∠ＡＣＦ＝90°
反対側の角度である∠ＢＣＥ＝180－90＝90°
以上から、１辺と両端角が等しく合同。

（２）

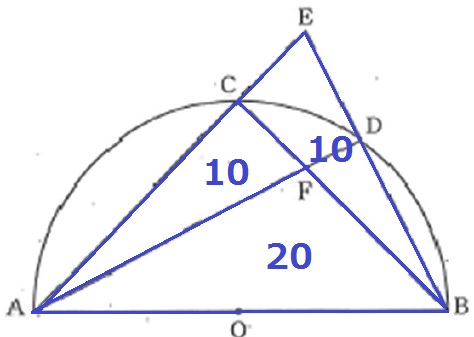
△ＡＢＥ＝40ｃｍ²、△ＡＢＦ＝20ｃｍ²
前問より△ＡＦＣ≡△ＢＥＣだから、おのおの10ｃｍ²。

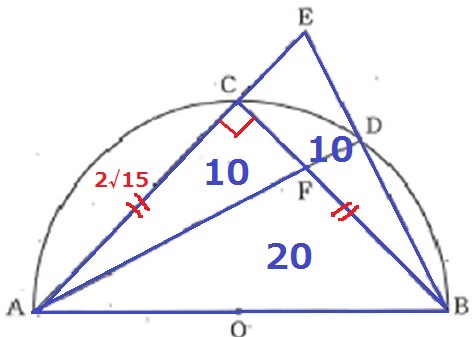
面積しかわかっていないので、どこかの長さを確定したい。
△ＡＢＣが直角三角形であることを利用しよう！
ＡＣ×ＡＣ÷２＝30
ＡＣ²＝60
ＡＣ＝２√15ｃｍ

ＣＦ：ＦＢは△ＡＣＦと△ＡＦＢの面積比に等しい。
ＣＦ：ＦＢ＝10：20＝①：②
ＡＣ＝ＢＣ＝③

△ＡＣＦで三平方。
ＡＦ²＝①²＋③²＝⑩²
ＡＦ＝〇√10

したがって、ＡＦの長さは、
２√15×√10/３
＝10√６/３ｃｍ

大問１
全問死守！
大問２
基本問題が多い。
（７）類題が去年のどこかの公立高校にありました。
大問３
愛媛はここで変なことをする。時間と台数の割合計算は正確に！
（２）②図を描くべし。１/３円→有名直角三角形の活用。
（３）解きにくい。ここも図を描いてとっかかりを掴む。
大問４
よくある数量変化の問題。
（３）コーナーを曲がると変化する。
（４）解説は算数で書きました。
大問５
この形もどこかの公立高校で見かけた。
（２）面積しかわかっていないので、確定できる長さに狙いを絞る。
直角が大きなヒント。
公立高校入試解説ページに戻る