平均38.0点(前年比;-4.1点)

問題はこちら→東進ハイスクールさん(解答)
出題範囲の縮小は資料の活用(標本調査)
大問1(小問集合)
(1) 93.4%
2×(-3)+1
=-6+1
=-5
(2) 88.6%
5/3a-3/4a
=11/12a
(3) 82.2%
x-3y=6
2x+y=5
これを解いて、x=3、y=-1
(4) 80.2%
6/√2+√8
=3√2+2√2
=5√2
(5) 77.6%
x2+x=6
x2+x-6
=(x+3)(x-2)=0
x=-3、2
(6) 83.4%
15a3b2÷5/2ab2
=6a2
(7) 62.9%
y=ax2に(x、y)=(4、6)を代入。
6=42a
a=3/8
y=3/8x2にx=-6を代入。
b=3/8×62=27/2
(8) 37.4%
1~6を用いる2桁の素数を調べる。
11、13、23、31、41、43、53、61
確率は、8/36=2/9
(9)アイ…23.3%!、最頻値…35.1%

それぞれの階級値は5分、15分、25分、35分。
平均値との差は-15分、-5分、+5分、+15分。
これらに各度数をかけ合わせて、すべて均すと20分になる。
-75-50=-125
平均未満が-125だから平均超は+125。
5×(ア)+60=125
ア…(125-60)÷5=13人
イ…5+10+13+4=32人
最頻値(モード)は最もあらわれている値。
13人いる20~30分の階級の階級値である25分。
ア…13、イ…32、最頻値…25分
大問2(空間図形)
(1) 32.1%!
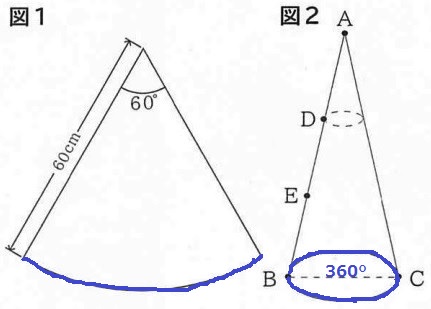
青線の長さが等しい。
円周の長さは直径×π、扇形の弧の長さは直径×π×60°/360°
⇒【扇形の直径:円の直径=360:60】
(*扇形の直径と円の直径は中心角の比の逆比)
扇形の直径は、60×2=120cm
直径BC…120×60/360=20cm
(2) 10.6%!
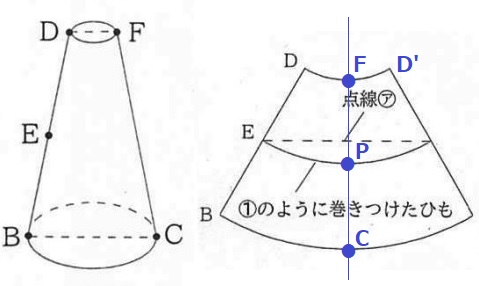
D~Fは円の半周なので、展開図では弧DD’の中点がFである。
Fの真下にPとCがある。
EはBDの中点、PはFCの中点。
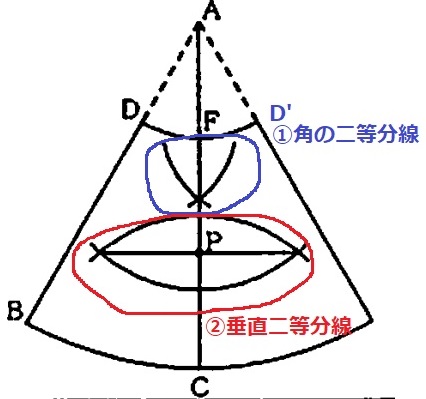
①∠DAD’の二等分線。
②FCの垂直二等分線。
交点がPである。
(3) 12.7%!
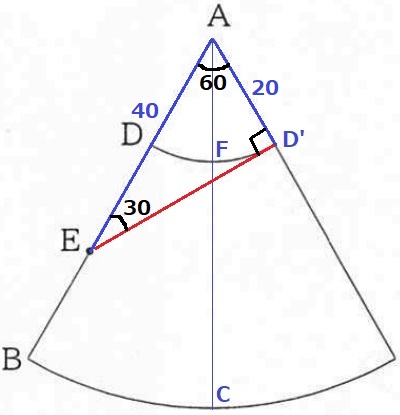
D’はDと同じ点。ED’が求めるべき長さ。
弧DD’とED’はD’で交わる。ED’はD’を接点とする弧DD’の接線である。
半径と接線は直交するから、∠AD’E=90°
△AD’Eで三平方(1:2:√3)→D’E=20√3cm
(4) 0.7%!!!
2周巻きます(;´・ω・)

ヒモを1直線にするために、線対称の要領で扇形をもう1つ追加する。
すると、FCを2回横切ってEに着く。

∠BAB’=120°
外側に直角三角形AGEを作る。
内角が30°-60°-90°だから、辺の比は1:2:√3。
AG=20cm、GE=20√3cm
△BEGで三平方。
BE2=802+(20√3)2=7600
BE=√7600=10√76=20√19cm

今年度の神奈川ラストで、別々のヒモで2度巻きつける問題がでました。
大問3(平面図形)
(1) 32.6%!
初問からやりにくい(;´Д`)
Cを中心とする円の円周上にA、B、P、Qがある。
AB、PQは円の直径。
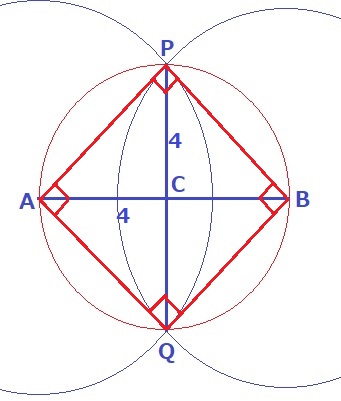
半円の弧に対する円周角は90°だから、4角すべてが90°となる。
直径AB=PQから対角線の長さも等しく、四角形AQBPは正方形である。
△ACPは直角二等辺三角形。辺の比は1:1:√2より、AP=4√2cm
AP=4√2cm、∠APB=90°
(2) 1.4%!!
何をどのような手順で記述すべきか。
証明の方針を立てる必要があり、一筋縄ではいかない。
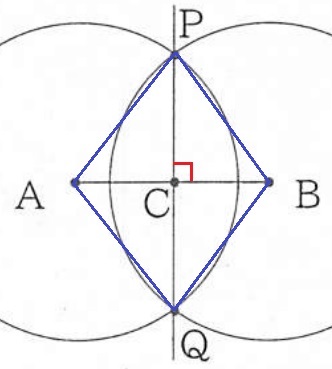
証明したいのはAB⊥PQ
∠ACP=90°を示したい。
∠ACP=∠BCPがわかれば、各々が90°となる。
∠ACP=∠BCPを導くには、△APC≡△BPCを証明する。
この証明には問題文の『対角線PQが∠APBを二等分する』点が必要である。
角の二等分を指摘するために、△APQ≡△BPQを先に証明する。
これらを逆から順に述べていく。

左図。
円の半径(仮定)よりAP=BP、AQ=BQ。共通辺PQ。
3辺が等しく、△APQ≡△BPQ
合同図形の対応する角から∠APQ=∠BPQ
よって、PQは∠APBの二等分線である。
右図。
半径と共通辺と等角より、2辺と間の角が等しく、△APC≡△BPC
対応する角の大きさは等しいから、∠ACP=∠BCP
∠ACP+∠BCP=2∠ACP=180°
∠ACP=90°より、AB⊥PQとなる。
(3) 14.0%!
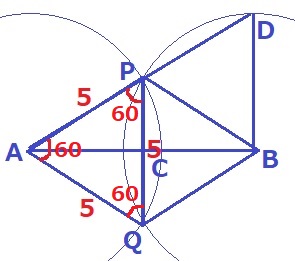
仮定と半径でAP=PQ=AQ
△APQは3辺が等しく正三角形。
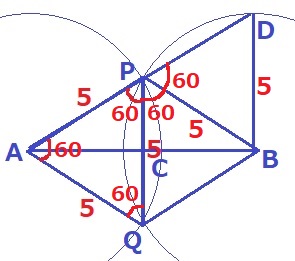
同様に、△BPQも正三角形で∠BPQ=60°
∠BPD=180-(60+60)=60°
△BDPは、半径でBD=BPで二等辺三角形。
∠BPD=60°より残りの角を調べると全て60°
△BDPは正三角形で、PD=5cm
大問4(平面図形)
(1) 36.7%
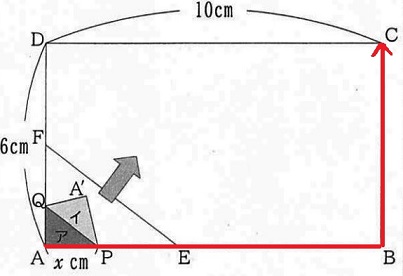
『はがし終えるまで』だから、Pは赤線のルートをたどる。
Pは16cm移動する。
0≦x≦16
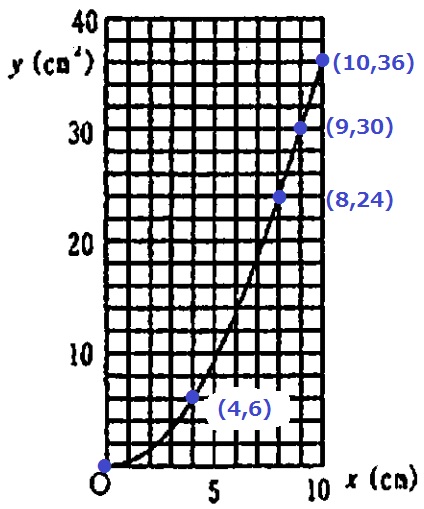
(2) 2.9%!!

はじめは縦:横=3:4を維持しながら、直角三角形の底辺と高さがともに伸びる。
→y=ax2で増加する。
AQ=6cmのときに形が変わる。
このとき、AP=8cm、y=8×6÷2=24cm2
x=8のとき、y=24だから、24=82a
a=3/8
0≦x≦8では、y=3/8x2のグラフとなる。
8≦x≦10では増加する部分は平行四辺形。高さは固定で底辺だけ伸びる→一次関数
x=10のとき、y=24+2×6=36
通過すべき格子点を意識する。
(3) 0.4%!!!
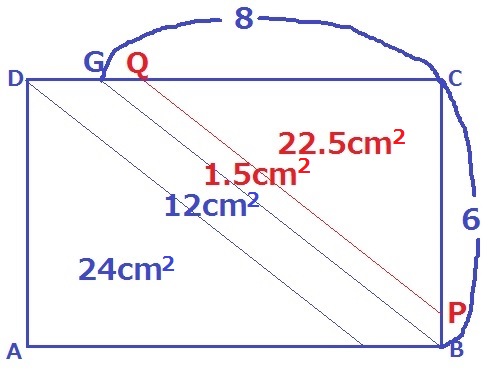
長方形の面積の5/8…6×10×5/8=37.5cm2
先ほどx=10のときに36cm2だったので、+1.5cm2すればいい。
辺DC上でCから8cm離れた点をGとする。
△CPQの面積は、24-1.5=22.5cm2
△CPQ∽△CBGの面積比からCP:CBを求める。
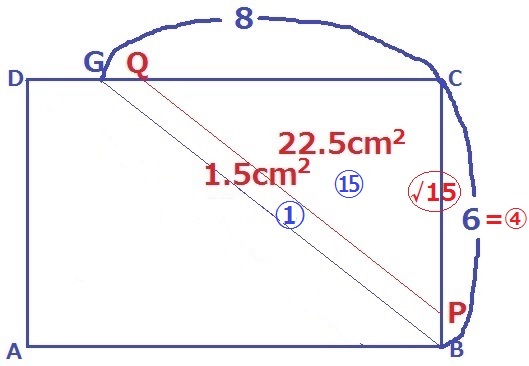
△CPQ:△CBG=22.5:24=15:16
相似比はCP:CB=√15:4
CP=6×√15/4=3√15/2cm
A~B~Cまでの距離が16cmなので、
Pが動いた距離は、x=16-3√15/2cm
(4) 0.1%!!!
むずかしい(´д`)
仕上げるのに時間がかかりました。

折り返しは折り目を対称の軸とすると左右対称である。
CがA’B’上にくるということは、Cを対称移動させたC’はAB上にある。
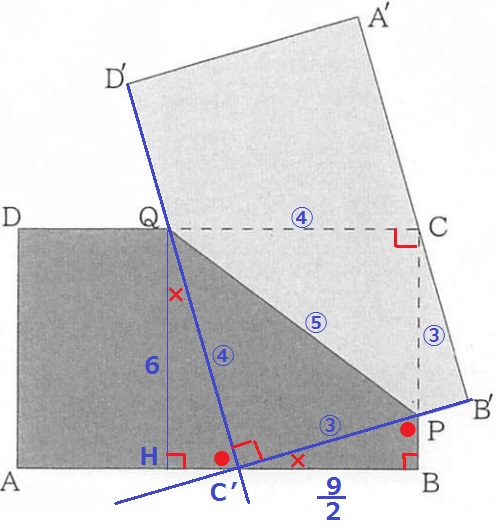
斜辺にあたるPQは平行移動するので、直角三角形の縦:横=3:4
まだ剥がされていない△PCQの辺の比は③:④:⑤で、対称図形の△PC’Qも③:④:⑤
しかし、③:④:⑤の相似ばかりに目がいくと、なかなか新しい数値が判明しない。
そこで、QからABに垂線をひき、足をHとして、別の相似を作成する。
●+×=90°の角度の調査で、2角が等しく△QHC’∽△C’BP
QH:C’B=QC’:C’P=④:③
C’B=6×3/4=9/2cm
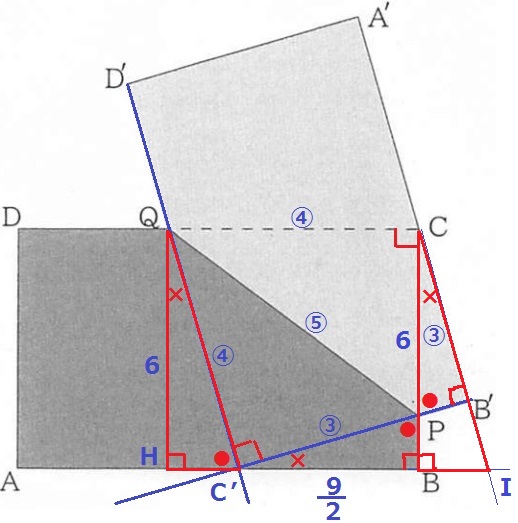
ABとA’B’を延長した交点をIとする。
右側で角度を調査すると、∠BCI=×
△QHC’と△CBIは1辺と両端角が等しいので合同。
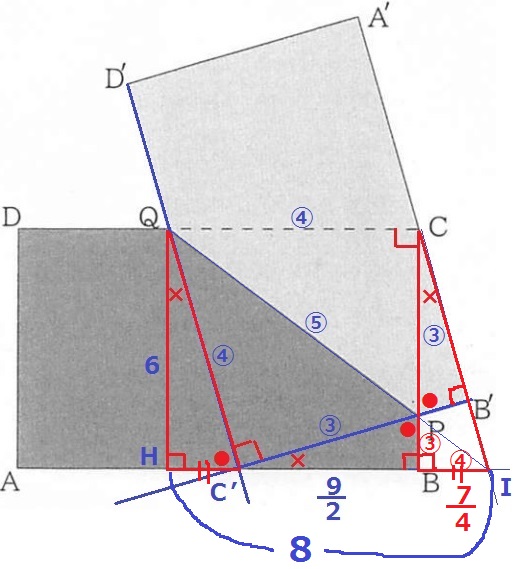
対称の軸であるQPの延長もIを通過する。
△QHIの縦:横=3:4だから、HI=8cm
合同でHC’=BI
BI=(8ー9/2)÷2=7/4cm
△PBIの縦横も3:4だから、PB=7/4×3/4=21/16cm
Pが動いた距離は、x=10+21/16=181/16
@別解@
YAさんから素晴らしい解法を頂きました。

QからA’B’に垂線、足をGとします。
△QCG∽△CPB’から、CB’=9/2cm
ここでPB’=aとします。
折り返しでPB=a
CP=6-a
△CPB’で三平方。
a2+(9/2)2=(6-a)2
12a=63/4
a=21/16
x=10+21/16=181/16
おそらく、こちらの解法が作問者の想定解だと思われます。
@別解2@
小田原の齋藤さんから素晴らしい解法を頂きました。
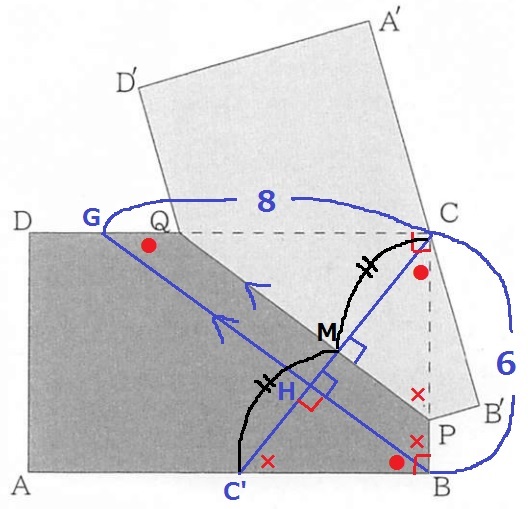
(3)のGを利用します。
折り目は平行を維持するのでGB//QP
CからGBに垂線をおろし、GB、ABとの交点をH、C’とします。
△GBCは辺の比が3:4:5の直角三角形。
∠BGC=●、∠GBC=×とおき、錯角や●+×=90°で角度を調査していくと、
△CC’B∽△GBCより、CC’=6×5/4=15/2cm
CC’とQPの交点をMとすると、MはCC’の中点にあたります。
折り目QPを対称の軸とするとCとC’は対応する点だからです。
CM=15/2÷2=15/4cm
△CPMも3:4:5ですから、CP=15/4×5/4=75/16cm
xの値は、AB+BC-CP=10+6-75/16=181/16
3:4:5を一貫して利用する、鮮やかな解法でした。
●講評●
80点以上の棒が見えないのだが。。
大問1
後半戦を考えると、ここで得点を確保したい。
(9)平均より上の合計と下の合計の和が同じ。階級値と平均の差で対処する。
大問2
(1)初問から3割を切る。
円錐の側面積である扇形の中心角は〔×底面の半径/円錐の母線〕で処理できるが、
これは半径(直径)と中心角の関係が逆比だからである。
(2)点の位置を正確に把握しないと間違える。F・P・Cはそれぞれの弧の中点にくる。
(3)接線がポイント。弧と線分は接点で交わる。
(4)描き方がわからないとどうしようもない。
糸を直線で表すには、扇形を対称させて鏡の世界をつくる。
大問3
(1)思考力が試される。
A、B、P、QはCから等距離にある。ここからCは正方形AQBPの中心にある。
(2)垂直二等分線の作図は菱形の対角線が垂直に交わることを利用するが、
この証明が問われた。正しい手順で指摘しなければならない。
大問4
(2)直角三角形から途中で平行四辺形に変わる。グラフは(4、6)を通る点に注意!
(3)なかなか容赦ない。折り目は平行を維持する。(2)からさらに1.5cm2剥がせばいい。
三角形の∽につなげると、相似比は√15:4になる。
(4)公立高校入試では難問の部類にはいる。
できなくても問題ないので、余裕がなければ見直しに費やしたほうが懸命である。


コメント