平均42.3点(前年比;+4.3点)

問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1) 83.9%
12-6÷(-3)
=12+2
=14
(2) 84.5%
1/2a-4/3a
=-5/6a
(3) 66.0%
-4A+3B+2A
=-2A+3B ←代入
=-2(4x-1)+3(-2x+3)
=-8x+2-6x+9
=-14x+11
(4) 60.7%
-15a2b÷3ab2×(-2b)2
=-15a2÷3ab2×4b2
=-20ab
(5) 54.7%
(√2-√3)2+√6
=2-2√6+3+√6
=5-√6
(6) 74.1%
x2=x+12
x2-x-12
=(x+3)(x-4)=0
x=-3、4
(7) 52.1%
y=-3x2は上に凸のグラフ。
x=-4のとき、最小値y=-48
x=0のとき、最大値y=0
-48≦y≦0
(8) 60.7%
5枚から2枚取る→5C2=10通り
積が2の倍数でもない、かつ3の倍数でもない。
→いずれの倍数でもない(5、7)のペアしかない。
確率は1/10
(9) 65.6%
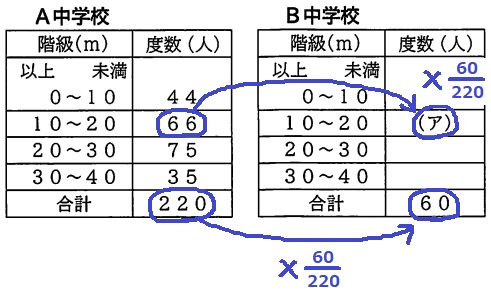
10~20mの階級の相対度数が等しい。
⇒(度数の合計)に対する(10~20mの度数)の割合が等しい。
【66/220=ア/60】
ア=66×60/220=18
大問2(関数)
(1)aの値…59.3%、3a+bの値…37.6%
直線が右下なので、傾きaは負の値。
問題は3a+b

切片が0より上にあるのでbは正の値。
a>0、b<0とちぐはぐな条件で3a+bの符号をどう求めればよいのか。
なんとなく傾きが45°以上だからa<-1っぽく、b<2っぽいので、負の気もしなくはないが…。
ax+bと3a+bを並べてみる。
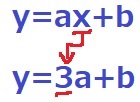
xが3に値する。
すなわち、x=3のときのyの値が3a+bである。
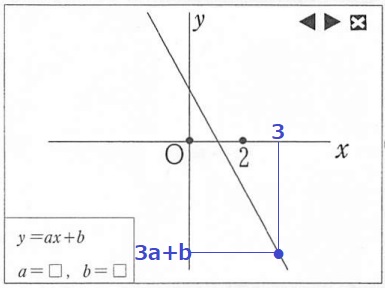
x=2のとき、yの値は負。
x=3のときも負なので、3a+bは負の値となる。
aの値…負の値、3a+b…負の値
(2) 27.7%!
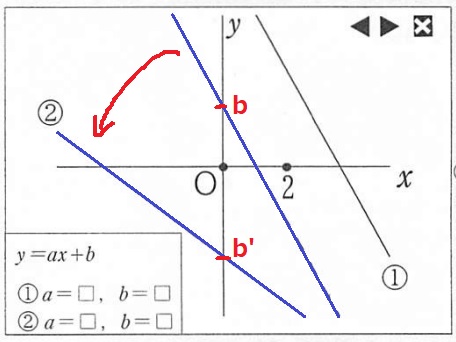
傾きが緩くなっている。
傾きを大きくすると直線は反時計回りにまわる(傾き-2→-1/2をimage)
切片bは下に移動しているので小さくなっている。
解答…aの値は大きくする、bの値は小さくする
(3) 8.4%!!
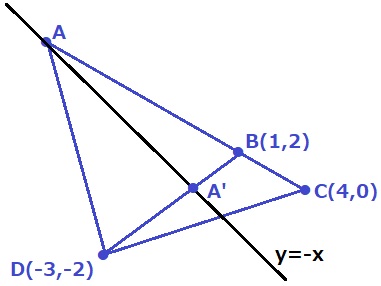
三角形となるAの位置を定める。
CBの延長上にAがあると、点BがAC上にきて△ACDになる。
もう1つはBD上にA’があると、△BCDになる。
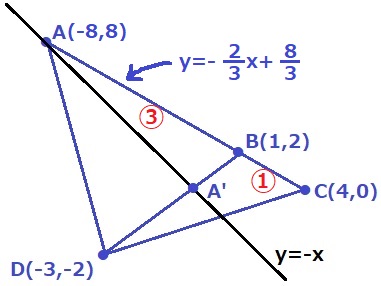
B(1、2)→C(4、0)
右に3、下に2なので、傾きは-2/3
y=-2/3x+bに(x、y)=(4、0)を代入すると、
0=-2/3×4+b
b=8/3
Aはy=-xとy=-2/3x+8/3の交点。
-x=-2/3x+8/3 ←3倍
-3x=-2x+8
x=-8
A(-8、8)
A・B・Cのx座標の差から、
AB:BC=9:3=③:①
S(△BCD):T(△ACD)
=BC:AC
=1:4
(4) 4.0%!!
説明問題。
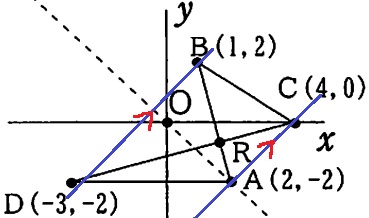
方針は立てやすい。
面積が等しいといえば等積変形。
傾きを調べてみると、ACとDBの傾きはいずれも1でAC//DB
等積変形で△ADC=△ABC
これらから共通部分△ARCを控除すると△RAD=△RBCとなる。
大問3(方程式・空間図形)
(1) 70.6%
友人の人数をx人として、ロールパンの数で等式を立てる。
余りは引き、不足分は足して帳尻を合わせる。
4x-9=6x+5
x=7
7人
(2)計算式…16.6%!、解答…27.4%
答案では求める過程も記述する。
求めたい食パンをx斤、ロールパンをy個とする。
留意点はロールパンは6個分の分量なので、
これを1個あたりになおすと小麦粉150/6g、バター10/6gになる(;´Д`)
小麦粉で等式。
300x+150/6y=1500 …①
バターで等式。
10x+10/6y=80 …②
①を整理すると、12x+y=60 …③
②を整理すると、6x+y=48 …④
これを解くと、x=2、y=36
食パン…2斤、ロールパン…36個
@余談@

本問は記述式なので仕方ないですけど、方程式の計算が面倒臭い。
解答が答えのみだった場合、なんとか回避できないものか。
食パン1斤の小麦粉が300gなので、最大で1500÷300=5斤つくれる。
ということは、食パンは1~4斤のいずれかなので全て調べてしまう。
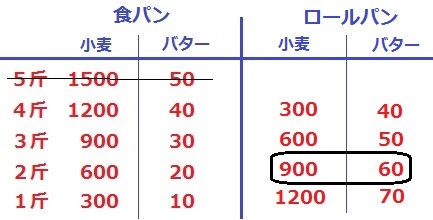
小麦は±300g、バターは±10gの増減。
ロールパンのなかで小麦:バター=150:10=15:1となる組み合わせは、
食パンが2斤のときである。
(3) 0.6%!!!
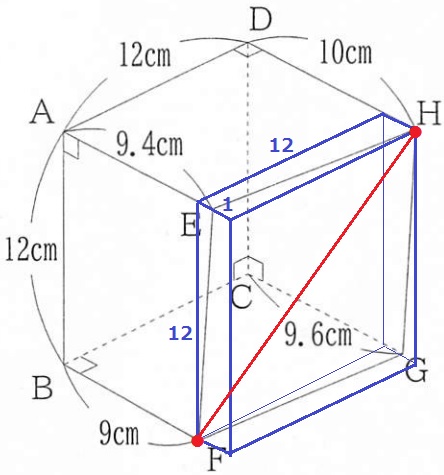
求めたいFHを対角線とする直方体を描く。
1辺がa、b、cの直方体の対角線→√(a2+b2+c2)
直方体の奥行きは、DH-BF=1cm
FH=√(122+122+12)
=√289=17cm
大問4(平面図形)
(1) 44.9%
半径2mの半円。
2×2×π÷2=2πm
(2) 3.3%!!
CPとDQを1辺とする三角形の合同、
すなわち、△APC≡△AQDを証明すればいい。
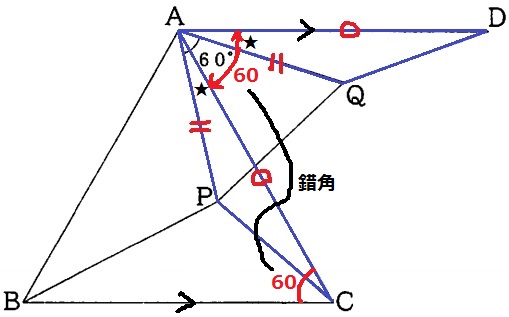
正三角形APQの1辺より、AP=AQ
正三角形ABCの1辺と仮定より、AC=BC=AD
AD//BCの錯角で∠BCA=∠DAC=60°
∠PAC=60-∠CAQ=∠QAD
2辺とあいだの角が等しいから、△APC≡△AQD
対応する辺の長さは等しいので、CP=DQ
(3) 8.8%!!
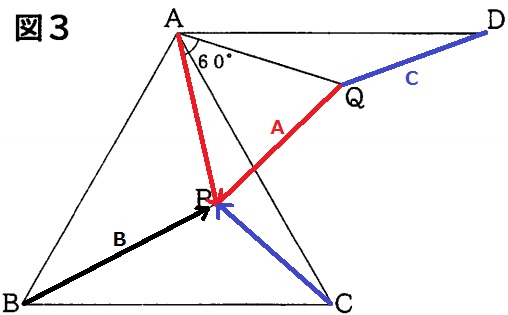
Aは赤、Bは黒、Cは青を移動する。
BPとPQとQDが一直線になれば、A・B・Cが移動する距離の和が最も短くなる。
△APQをもう少し時計回りにまわすとまっすぐになりそう。
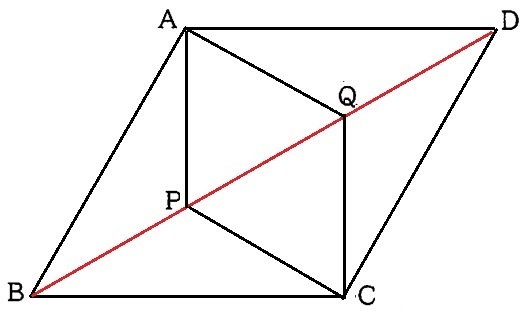
AD//BC、AD=BCより、四角形ABCDは1組の対辺が平行でかつ長さが等しい
⇒平行四辺形ABCD
さらに、正三角形ABCからAB=ADで隣り合う辺が等しい
⇒菱形ABCD
BDは菱形ABCDの対角線である。
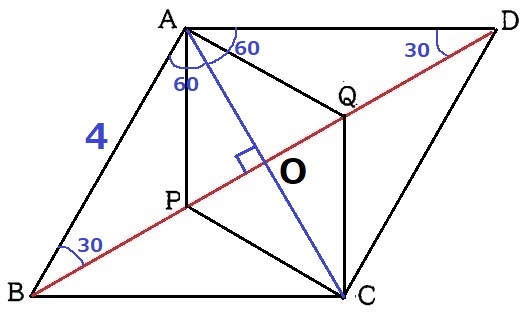
ACとBDの交点をOとする。
菱形の対角線は直交するので∠AOB=90°
△ABOは内角が30°—60°—90°で辺の比は1:2:√3
BD=2BO=(4×√3/2)×2=4√3m
(4) 0.9%!!!
先生のアドバイスによると、∠APB=∠BPC=∠CPA=120°のときに
AP+BP+CPが最短になるらしい。。
正三角形は特別な三角形なので、平凡な三角形でもう一度おさらいします。

△APCを反時計回りに60°回転させて△AP’C’をつくる。
AP+BP+CPはBP+PP’+P’C’となり、
BC’が一直線になるとき、題意に適するPが得られる。
△APP’は正三角形なので、∠APB=∠AP’C’=180-60=120°
∠APC=∠AP’C’=120°で、残りの∠BPC=360-240=120°となる。
ようするに、三角形の内部で120°をつくることがポイントとなる。
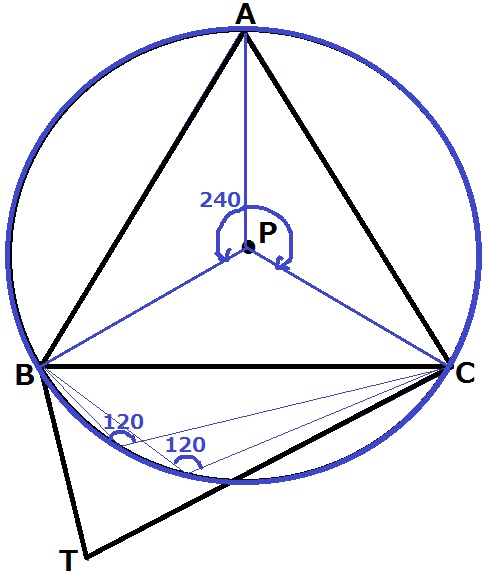
△ABCの外接円を描く。
∠BPC=240°だから、この円周角は120°である。
この円周上かつ△BCTの内部のどこかにRがある。

ここで、△BCTが二等辺三角形であることに着目する。
△CRBと△CRTは左右対称で合同。
対応する角で∠BCR=∠TCRだから、Rは∠BCTの二等分線上にある。
まとめると・・
①中心Pから△ABCの外接円を描く。
②∠BCTの二等分線。
これらの交点がRとなる。
@余談@
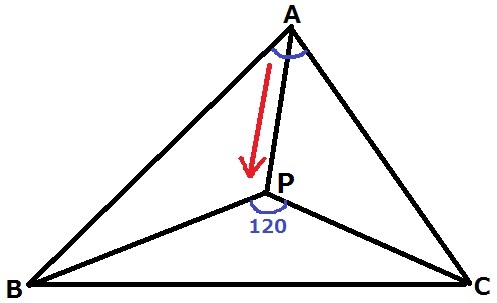
『3つの角の大きさがすべて120°未満の三角形のときに成り立つ』
どうしてかというと、Aを下へひっぱると∠BPCは必ず∠Aより大きくなるので、
仮に∠A=120°だと∠BPC>120°になってしまう。
つまり、∠BPC=120°となるPは△ABCの内部に存在しない。
@フェルマー点@
どうやら数学の世界ではフェルマー点とよぶそうです。
フェルマー点Fはいくつかの性質をもっています。
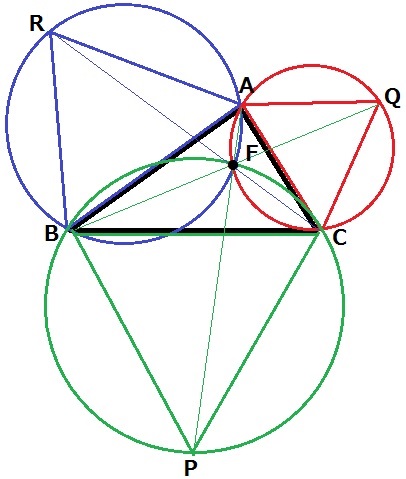
△ABCの各辺を1辺とする正三角形を追記。
この3つの正三角形の外接円はフェルマー点で交わる。
さらに、うえのようにAP、BQ、CRを結ぶとフェルマー点で交わる。
中学生レベルの数学で証明できますので、一考してみてください。
本問ではBTを1辺とする正三角形BTSをつくり、ATとCSの交点からもRを作れる。
ちなみに、∠A≧120°の場合は、頂点Aがフェルマー点になるそうです。
●講評●
大問1
(8)該当する組み合わせは1つしかなかった。
(9)やや変わった出し方だが、分数に持ち込むと見えやすい。
大問2
(1)落とし穴だったと思う。
3a+bの値はyの値であることに気づけるか。
ここで下手に時間を使うと後半戦が危うくなる。
(3)四角形を三角形にする→1つの頂点がどこかの辺上にくる。
計算は手早く処理したい。
(4)2直線の平行→等積変形で2つの三角形が等しい。
これらから共通部分を引いたものも等しい。
大問3
(2)1個あたりに直すタイプは他県でも見かける。分数がやらしい。
(3)切り口や数値がやらしいが、答えは整数であった。
大問4
高度な思考力が問われた。要点を外さないこと!
(3)AP+BP+CPの3つの線分はどこに移ったか。
これらが直線になったとき、どのような性質をもつ図形となるか。
正三角形の内角60°を手がかりにする。
(4)難問。
△BCT内部に120°をつくることをおさえる。
これがわかっても難しい(;`ω´)
おもしろい問題なので、どこかの問題集に載らないかな。



コメント