問題PDF
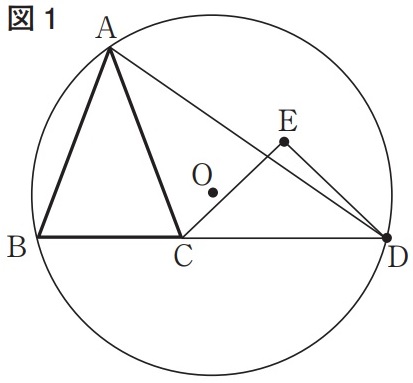
上の図1で、△ABCは、AB=ACの二等辺三角形である。
点Dは、線分BCをCの方向に延ばした直線上にある点である。
頂点A、頂点B、点Dを通る円を円Oとする。
点Eは、円Oの内部または円周上の点で、直線BCについて頂点Aと同じ側にあり、
2点C、Dからの距離が等しい点である。
点Aと点D、点Cと点E、点Dと点Eをそれぞれ結ぶ。
(1)
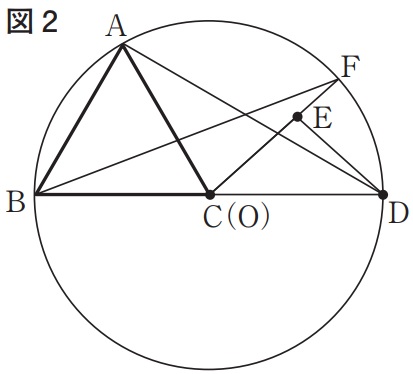
上の図2は、図1において、点Eが円Oの内部にあり、
頂点Cが点Oに一致するとき、線分CEをEの方向に延ばした直線と円Oとの交点をFとし、
頂点Bと点Fを結んだ場合を表している。
AC:CE=√2:1のとき、∠ABFの大きさは何度か。
(2)
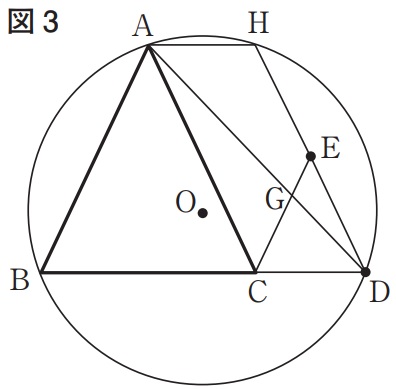
上の図3は、図1において、点Eが円Oの内部にあり、BC:CD=2:1、
∠BAC=∠CEDとなるとき、線分ADと線分CEとの交点をG、
線分DEをEの方向に延ばした直線と円Oとの交点をHとし、
頂点Aと点Hを結んだ場合を表している。
四角形ABDHと△GCDの面積の比を最も簡単な整数の比で表せ。
(3)
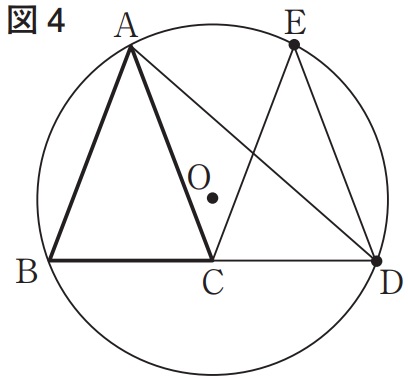
上の図4は、図1において、BC=CD、∠BAC=∠CEDとなる場合を表している。
点Eは、円Oの周上にあることを証明せよ。
@解説@
(1)
角の情報が見当たらない。

AB=AC、円の半径から△ABCは正三角形→∠ABC=60°
AC:CE=√2:1
√2と1といえば、どこかに直角二等辺三角形があると予想する。
半径でCD=√2、△ECDの辺は1:1:√2で直角二等辺三角形→∠ECD=45°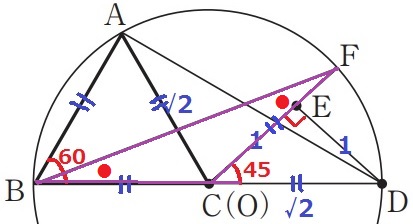
△BCFは二等辺三角形。
外角定理を適用して、∠FBC=45÷2=22.5°
∠ABF=60-22.5=37.5°
(2)
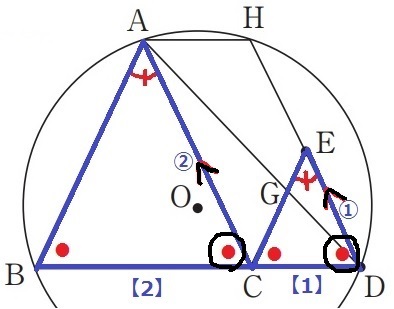
△ABCと△ECDは二等辺三角形。
おのおのの頂角が等しいので、底角(●)も等しい。
2角が等しく、△ABC∽△ECD
AC:ED=②:①
また、∠ACB=∠EDCの同位角が等しいからAC//HD
…なんとなく、AHとBDも平行っぽい。
これをどうやって説明すべきか。
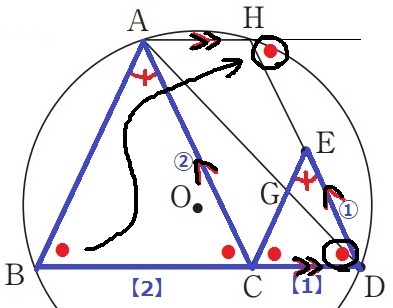
ここで円に注目する。
四角形ABDHは円に内接しており、内接四角形の内角はその対角の外角に等しい。
∠ABD(●)を上図のように移動させ、等しい錯角からAH//BD
2組の対辺が平行ゆえ、四角形ACDHは平行四辺形である。

△ACG∽△DEGより、AG:GD=2:1
△GCDの面積を1とすると、△ACG=2
ADは平行四辺形ACDHの対角線で、△ACD=△DHA=3
BC:CD=△ABC:△ACD=2:1から、△ABC=6
四角形ABDH:△GCD=12:1
(3)
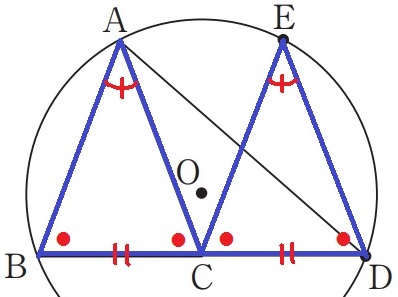
△ABCと△ECDは頂角が等しい二等辺三角形。
→おのおのの底角(●)が等しい。
BC=CDと合わせ、一辺と両端角が等しいので合同。
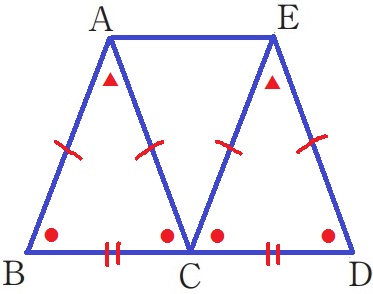
AB=AC=EC=ED
AEを結ぶ。
四角形ABDEが円に内接すると指摘できれば、
点Eは円Oの周上にあるといえる。
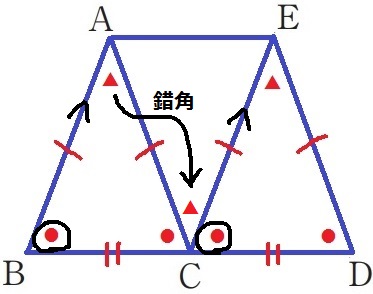
∠ABC=∠ECDより、同位角が等しいのでAB//EC
錯角で∠BAC=∠ECA(▲)
2辺とあいだの角が等しいから、△ABC≡△CAE(≡△ECD)
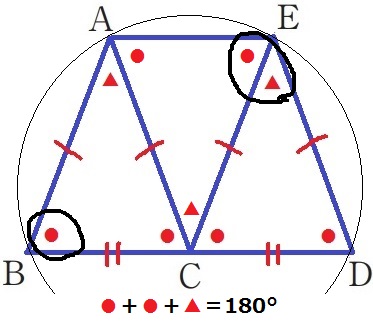
対応する角で、∠CEA=●
△ABCの内角から、●+●+▲=180°
∠ABD+∠DEA=●+(●+▲)=180°
対角の和が180°だから四角形ABDEは円Oに内接するので、
点Eは円Oの周上にある。
@別解@
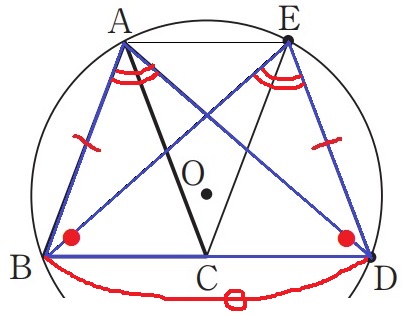
公式解答では、△ABC≡△ECDを指摘したあとでBEを結び、
2辺とあいだの角から△ABD≡△EDB
対応する角で∠BAD=∠DEB
AとEは直線BDについて同じ側にあることから、
円周角定理の逆を使ってEが同一円周上にあると証明しています。



コメント