問題ＰＤＦ
Ｓ＝ｎ⁴－５ｎ³－10ｎ²＋35ｎ＋49について、
次の問いに答えなさい。

（１）
を展開しなさい。

（２）
とするとき、 をｔの式で求めなさい。

（３）
Ｓを因数分解しなさい。

（４）
Ｓ＝－26のとき、ｎの値を求めなさい。
ただし、ｎは自然数とする。

）

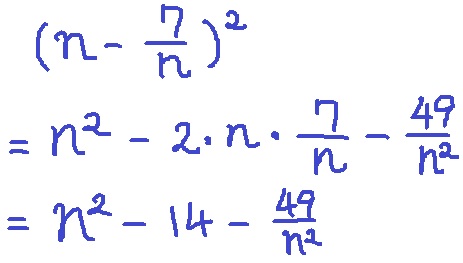
ｎ²－14＋49/ｎ²

（２）
まずはＳ÷ｎ²を算出。

ここで前問を活用する。
ｔ²＝（ｎ－７/ｎ）²＝ｎ²－14－49/ｎ²←この形を作れないかを考える。

*－10＝－14＋４にして－14を作る。
ｔ²の形で整理するとｔも見える。するとｎがなくなる。
Ｓ/ｎ²＝ｔ²－５ｔ＋４

（３）
前問の利用。
Ｓ/ｎ²＝ｔ²－５ｔ＋４＝（ｔ－１）（ｔ－４）

２行目：ｎ²＝ｎ×ｎに分解して、それぞれのカッコにｎをかけあわせる。
すると、分母のｎが払われる。
Ｓ＝（ｎ²－ｎ－７）（ｎ²－４ｎ－７）

（４）
前問利用。
Ｓ＝－26＝－１×26＝－26×１＝－２×13＝－13×２

ｎは自然数なので、（ｎ²－７）－ｎ＞（ｎ²－７）－４ｎ
ｎ²－ｎ－７＞ｎ²－４ｎ－７
◆26×（－１）のとき（ｎ²－ｎ－７＝26、ｎ²－４ｎ－７＝－１）

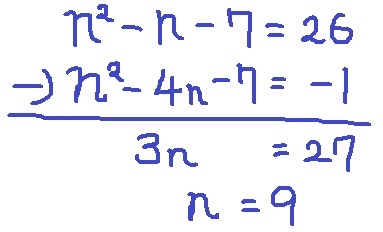
しかし、ｎ²－ｎ－７にｎ＝９を代入しても26にならない。
ｎ²－４ｎ－７に代入しても－１にならない。×

◆１×（－26）のとき
同様にｎ＝９で、代入すると×。

◆13×（－２）のとき

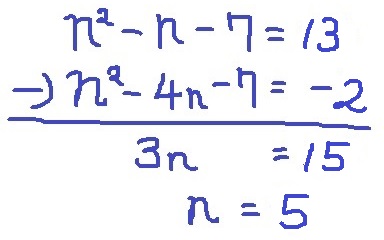
ｎ＝５を代入してみる。
ｎ²－ｎ－７＝５²－５－７＝13
ｎ²－４ｎ－７＝５²－４×５―７＝－２〇

◆２×（－13）
ｎ＝５だが、代入してもダメ×

したがって、ｎ＝５
国私立高校入試解説ページに戻る