問題ＰＤＦ
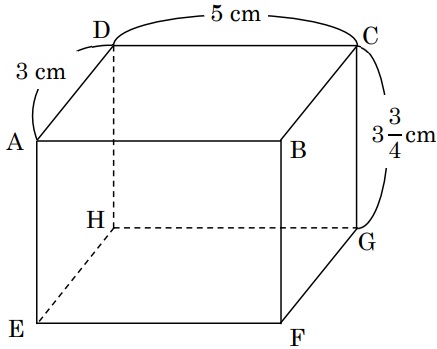
下の図のような直方体ＡＢＣＤ―ＥＦＧＨがあり、直線ＤＧの長さは25/４ｃｍです。
（１）
面ＡＢＣＤを辺ＢＣの周りに１回転させるとき、
面ＡＢＣＤが通る部分の体積は何ｃｍ3ですか。
（２）
直方体を３点Ａ、Ｄ、Ｆを通る平面で切った切り口を辺ＢＣの周りに１回転させるとき、
切り口が通る部分の体積は何ｃｍ3ですか。
（３）
直方体を３点Ａ、Ｃ、Ｆを通る平面で切った切り口を辺ＢＣの周りに１回転させるとき、
切り口が通る部分の体積は何ｃｍ3ですか。
（１）
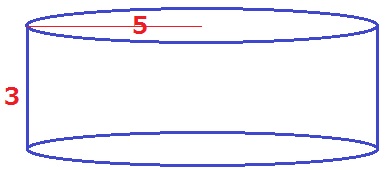
円柱。
５×５×3.14×３＝235.5ｃｍ3
（２）
ややこしいが難関中では出題される。
３点Ａ、Ｄ、Ｆを通る平面で切ると、断面は長方形ＡＦＧＤである。
これをＢＣを軸として１回転させると、高さ３ｃｍのドーナツ円柱になる。
底面積が知りたい。点ＢとＡＦの関係に注目する。
ドーナツの外径は、Ｂから最も遠いＡとの距離５ｃｍ。
ドーナツの内径は、ＢとＡＦとの最短距離、
すなわち、ＢからＡＦに垂線をおろし、交点をＩとするとＢＩである。
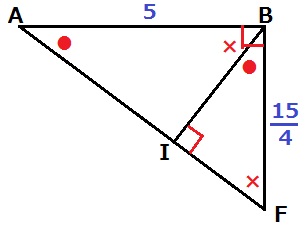
●＋×＝90°でおなじみの角度調査。
直角三角形ＡＦＢとＡＢＩとＢＦＩはすべて相似。
ここで、ＡＢ：ＢＦに注目すると、５：15/４＝４：３！
斜辺以外の比が３：４だから、直角三角形の辺の比はいずれも３：４：５である。
△ＡＢＩの辺の比より、ＢＩ＝３ｃｍ
したがって、求積すべき立体の体積は、
（５×５－３×３）×3.14×３＝48×3.14＝150.72ｃｍ3
（３）
３点Ａ、Ｃ、Ｆを通る平面で切り、ＢＣを軸として回転させると、
大きい三角錐から中にある小さい三角錐（空洞部分）をひいた立体になる。
これに（２）のドーナツ円柱を重ねてみると共通部分はだいぶ少ないが、
底面積は同じドーナツで、高さも３ｃｍで等しい。
ということは、柱÷３＝錘が使える。
（*ドーナツ柱÷３＝ドーナツ錐）
したがって、150.72÷３＝50.24ｃｍ3
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント