問題PDF
高校生のNさんは、夏休みに母校の中学校で数学の学習補助のボランティア活動に参加した。Nさんは、そこで中学生の太郎さんがノートに次のような計算をしているのを見付けた。Nさんは間違っているところに×を書いた。

太郎さんは、![]() になると勘違いしており、そのためアの計算には間違ったところがある。Nさんは、太郎さんが同様の勘違いでイの計算を行ったと考え、太郎さんのノートの4行目のところで×を付けようと思ったが、正しく計算した答えと同じになるため×を付けることができなかった。Nさんは、aが正の整数、bが正の数のとき、太郎さんのノートの3行目から4行目の計算のように
になると勘違いしており、そのためアの計算には間違ったところがある。Nさんは、太郎さんが同様の勘違いでイの計算を行ったと考え、太郎さんのノートの4行目のところで×を付けようと思ったが、正しく計算した答えと同じになるため×を付けることができなかった。Nさんは、aが正の整数、bが正の数のとき、太郎さんのノートの3行目から4行目の計算のように![]() となる例が他にもないか調べてみたところ、Nさんは、a=10のとき、b=(あ)となるのを見付けた。
となる例が他にもないか調べてみたところ、Nさんは、a=10のとき、b=(あ)となるのを見付けた。
〔問1〕
(あ)に当てはまる値を求めよ。
次に、Nさんは中学生の花子さんがノートに次のような式の展開をしているのを見付けた。
Nさんは、間違っているところに×を書いた。

花子さんは、x、yがどんな値でも、(x+y)2がx2+y2に、(x+c)(x+d)がx2+cdになると勘違いしており、そのためウの式の展開には間違ったところがある。Nさんは、花子さんが同様の勘違いでエの式の展開を行ったと考え、花子さんのノートの4行目のところで×を付けようと思ったが、×を付けることができなかった。Nさんは、花子さんの勘違いによる式の展開と、正しく式の展開をしたときの結果が同じになるときは、どんな場合か興味をもった。
e、f、gを自然数としてf>g、x≠0とすると、Nさんは、(x+e)2-(x+f)(x+g)を花子さんの勘違いによる方法で展開したときと、正しく展開したときの結果が同じになるときは、(x+e)2-(x+f)(x+g)=Aとしたとき、√Aが必ず自然数になることに気が付いた。
〔問2〕
上記の下線部が正しい理由を、文字x、e、f、g、Aを用いて説明せよ。
ただし、説明の過程が分かるように、途中の式や考え方なども書け。
なお、2つの数X、Yについて、【表】で示される関係が成り立ち、オ~ケには偶数か奇数のどちらかが入る。
説明するときに【表】のオ~ケに偶数か奇数を正しく当てはめた結果については、証明せずに用いてよい。

Nさんは、誤った計算方法でも正しい答えが出てくる場合について、他にどのような例があるか調べたところ、hを1以上9以下の整数、i、jをそれぞれ0以上9以下の整数としたとき、(h+i+j)3=100h+10i+jとなる場合があることが分かった。
そこでNさんは、kを1以上9以下の整数、ℓ、m、nをそれぞれ0以上9以下の整数として、(k+ℓ+m+n)4の値がk、ℓ、m、nを左から順に並べた4桁の数と等しくなる場合があるか考え、そのようなk、ℓ、m、nの組を見付けることができた。
〔問3〕
Nさんが見付けたk、ℓ、m、nについて、![]() の値を求めよ。
の値を求めよ。
@解説@
〔問1〕
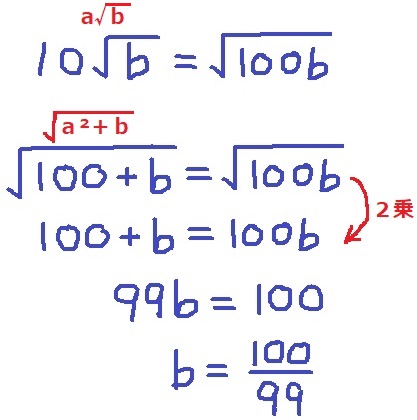
100/99
〔問2〕
難しい(;`ω´)
(x+e)2-(x+f)(x+g)=Aとして、これを正しい方法で展開したときと花子の勘違いの方法で展開したときに結果が同じになる場合、√Aが自然数になることを証明する。
→√Aが自然数ということは、Aは平方数である。
2通りで展開してみる。
【正】
(x+e)2-(x+f)(x+g)
=x2+2ex+e2-x2-(f+g)x-fg
=e2+2ex-(f+g)x-fg
【誤】(花子の勘違い)
(x+e)2-(x+f)(x+g)
=x2+e2-x2-fg
=e2-fg
これらが同じ値になるから、
e2+2ex-(f+g)x-fg=e2-fg
2ex-(f+g)x=0
2ex=(f+g)x ←x≠0だから÷xができる
e=(f+g)/2
これを元の式のeに代入してみる。
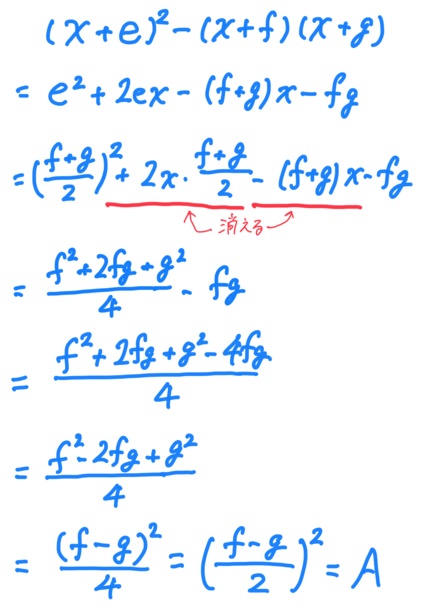
f、gは自然数でf>gだから、f-gは自然数である。
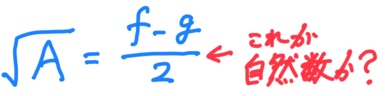
ここで、e=(f+g)/2→2e=f+gよりf+gは偶数。

f+gが偶数だと、f・gはともに偶数か奇数。
f・gがともに偶数か奇数であれば、f-gは必ず偶数である。(キ・ク)
→(f-g)/2は自然数である→√Aは自然数。
@@
公式解答を貼り付けておきます。

公式では、花子の方に代入していました。
確かに値が同じになるので、e2-fgの方が計算しやすいですね。
〔問3〕
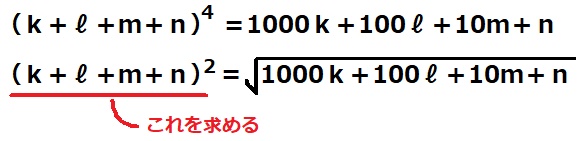
各位の和を4乗した数がその数自身になる。
その平方根なので、各位の和を2乗した値が答えになる。
今までとテイストが異なるため、前問を足掛かりにできない。
(k+ℓ+m+n)4={(k+ℓ+m+n)2}2が4桁になる。
2桁×2桁=4桁となる範囲を絞る。
30×30=900(←3桁)に当たりをつけると、(k+ℓ+m+n)2は31以上の2桁の平方数である。
→(k+ℓ+m+n)2は36、49、64、81のいずれか。
(*k+ℓ+m+nは6、7、8、9のいずれか)
4通りしかないので調べ上げる。
362=1296 →位の和が10以上になる。104=10000で5桁になってしまう。×
492=2401 →位の和が7。OK
642=4096 →10以上
812=6561 →同上
(k+ℓ+m+n)2=49


コメント