問題PDF
下の図のような道に沿って、地点Aから地点Bまで進みます。

次の問いに答えなさい。
(1)
図Ⅰの道を、右、上のどちらかの方向に進むとき、行き方は全部で何通りありますか。
(2)
図Ⅱの道を、右、上、右ななめ上のどれかの方向に進むとき、行き方は全部で何通りありますか。
@解説@
(1)
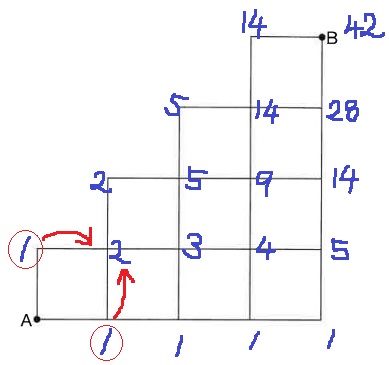
左と下を合わせていく。
機械的に調べていくと42通り。
@カタラン数@
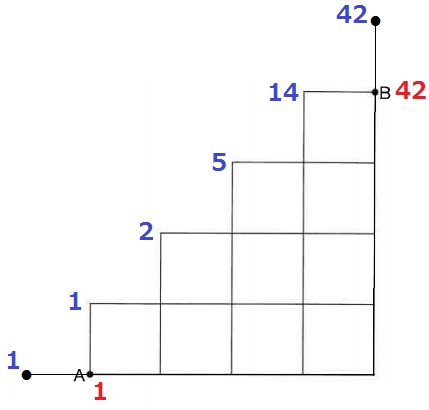
【1・2・5・14・42・132・429…】
この数列はカタラン数といい、中学受験の世界にもたびたび登場する。
階段状の最短経路にはカタラン数があらわれる。
これを知っていると42通りとすぐだせる。
132くらいまで覚えておくと便利かも。
では、なぜ42になるのか?(´~`)
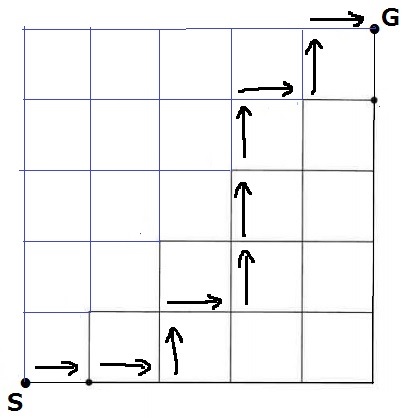
わかりやすいように、左上を足して全体を正方形にする。
S⇒Gは5つの→、5つの↑の並び替えで求められるから、
10C5=252通り
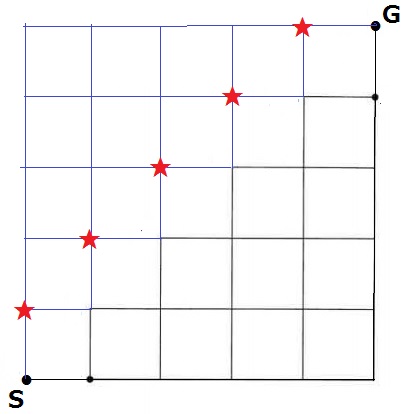
全体の252通りから、少なくとも1つの★を通過する左上ルートを引けば、
カタラン数42がでてくるはず。
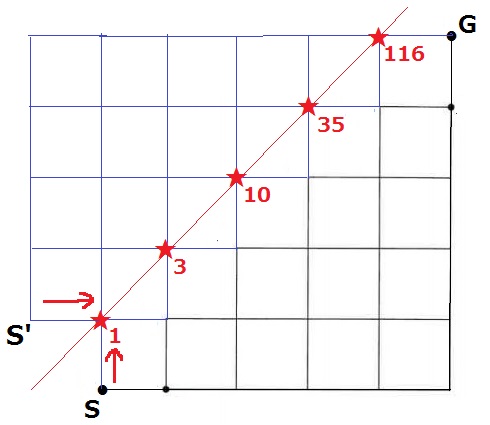
★のラインを対称の軸として線対称のルートを作成。
SとS’は対応するので、★までの場合の数がすべて等しい!
S’⇒Gは必ず1つの★を通り、6つの→、4つの↑だから、10C4=210通り
階段上のS⇒Gは、252-210=42通り
以上をまとめると、5番目のカタラン数は
10C5-10C4=42で求められた。
カタラン数Cn=2nCn-2nCn-1となり、
これを高校数学でチャッチャカチャーと処理すると、
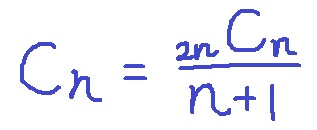
となります。
6番目のカタラン数は、
C6=12C6/7=132




コメント