問題PDF
(1)
次の計算をしなさい。
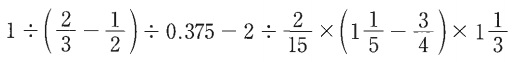
(2)
まっすぐな道路の片側に木を植えます。
最初にA地点とB地点に木を植えて、すべての木と木の間かくが等しくなるように、
A地点とB地点の間に木を植えることにします。
木の本数は、10mおきに植えるときのほうが、14mおきに植えるときより22本多く植えられます。
次の問いに答えなさい。
①A地点とB地点は何m離れていますか。
②10mおきに植えるときと、14mおきに植えるときに、
同じ位置に木を植えられるのは、A地点とB地点を除いて何か所ありますか。
(3)
太郎君は3種類のお菓子A、B、Cを合計2021個もらいました。
それぞれのお菓子の個数の比は、AとBは1:6、BとCは8:5です。
次の問いに答えなさい。
①太郎君はお菓子Aとお菓子Cをそれぞれ何個もらいましたか。
②お菓子をもらった日、太郎君はお菓子Aを20個とお菓子Cを180個家族にあげました。
その翌日から、太郎君は1人で毎日お菓子Aを2個とお菓子Cを3個食べ続けました。
何日間か食べたところ、お菓子Aの残りとお菓子Cの残りの個数の比が1:5になりました。
太郎君はお菓子を何日間食べましたか。
(4)
図のように直角三角形ABCと直線ℓが2点D、Eで交わっています。
直角三角形ABCを直線ℓの周りに1回転させてできる立体の体積を求めなさい。
ただし、円すいの体積は(底面積)×(高さ)÷3で求めるものとします。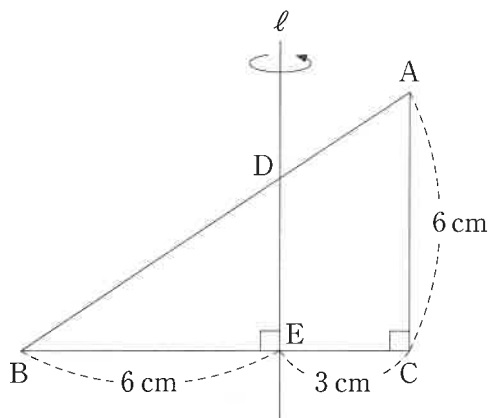
(5)
図は1辺4cmの正方形と、半径2cmで中心角90°のおうぎ形を4つ組み合わせた図形で、
辺AD上にAM=1cmとなるような点Mをとります。
また、辺BC上のFとCの間に点Pをとり、2点M、Pを結び、
図のように影のついた部分をそれぞれア、イ、ウとします。
次の問いに答えなさい。
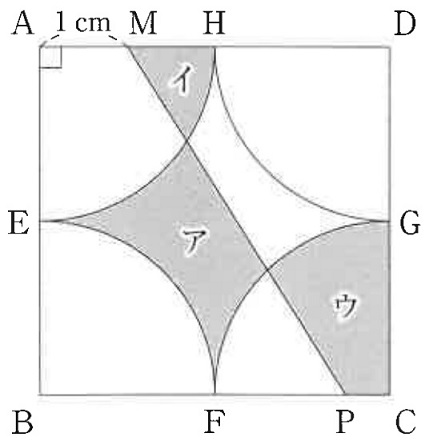
①CP=1cmのとき、ア、イ、ウの面積の和を求めなさい。
②アの面積と、イとウを合わせた面積が等しいとき、CPの長さを求めなさい。
@解説@
(1)
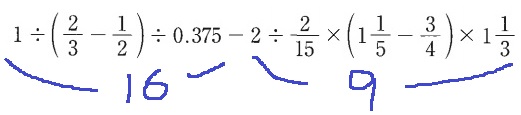
16-9=7
*375=125×3、125/1000=1/8→0.375=3/8
ここの1番は例年、答えが整数値です。
(2)①
A~Bにおいて、14mおきの間の数を●、10mおきの間の数を▲とする。
A~Bの距離で等式を立てると、14×●=10×▲
間の数の比は逆比で、●:▲=10:14=⑤:⑦
22本多く植えられる→間の数が22個多い。
差の②が22個に相当するので、10本おきの間の数▲=22×⑦/②=77個
A~Bの距離は、10×77=770m
②
10と14の最小公倍数は70。
A地点から70mおきに同じ位置に木を植えられる。
770÷70=11ヶ所
最後はB地点でかぶるので除くこと!
答えは10ヶ所
(3)①
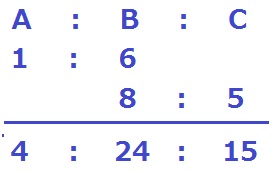
連比処理にかけると、A:B:C=④:㉔:⑮
和の㊸が2021個に相当する。
43×47=2021←年度問題。対策しておく。
A…2021×④/㊸=47×④=188個
C…2021×⑮/㊸=47×⑮=705個
②
A残り…188-20=168個
C残り…705-180=525個
ここから1日あたりAは2個、Cは3個ずつ減っていく。
求める日数までに減った総数(1日に減る個数×日数〇)の比をA:C=②:③とおくと、
(168-②):(525-③)=1:5
(168-②)×5=840-⑩=525-③
⑦=315
①=45
〇が日数なので、45日間
(4)

↑回転体はこのようになる。
円錐と円柱が重なり、上部に空白の小さな円錐がある。
△ABCの△DBEの相似から、DE=4cm

さらに長さを調べていく。
下の大きい円錐を区切ってみると、●はBDの中点にあたる。
立体の体積は、半径6高さ4の円錐と半径3高さ4の円柱の和から、
重複する半径3高さ2の円錐と上部空白の半径3高さ2の円錐を引けばいい。
6×6×3.14×4÷3+3×3×3.14×4-3×3×3.14×2÷3×2
=72×3.14=226.08cm3
(5)①
とても面白い問題です(´ω`)
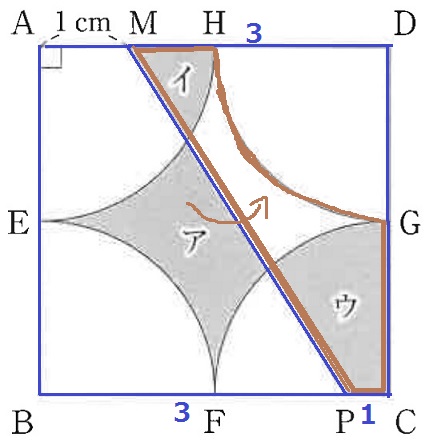
CP=AM=1cmのとき、図形全体が点対称である。
アを右へ引越し。
赤線のエリアが求積すべきエリアであり、
台形MPCDから半径2cmの4分の1円を引けばいい。
(3+1)×4÷2-2×2×3.14÷4
=4.86cm2
②

黒い部分を共通部分として巻き込むと、
ア+黒(台形ABPM)=イ+ウ+黒(4分の1円×3)
台形MPCDの面積は、正方形-台形ABPM=正方形全体-4分の1円×3
=4×4-2×2×3.14×3/4=6.58cm2
PCの長さは、6.58×2÷4-3=0.29cm
@余談@
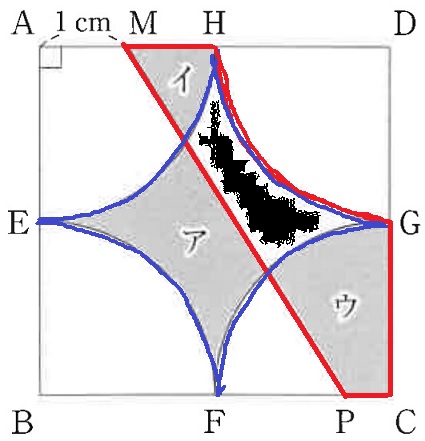
最初は、ア・イ・ウに囲まれているこちらを巻き込んで考えました。

ア+黒は✨みたいな形。
✨は正方形全体から扇形4つ引いたもの。
一方、イ+黒+ウは台形から扇形1つを引いたもの。これらが等積である。

もっと整理すると、正方形全体から扇形3つを引いたものが台形MPCDとわかる。
なぜ扇形3つが左の台形になるのか?そのワケを探したら先の解法を見つけました。



コメント