問題PDF
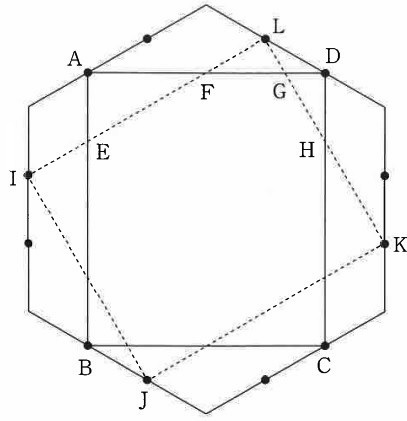
図のような正六角形があります。
辺の途中にある黒い点はそれぞれの辺を3等分する点で、正六角形の面積は54cm2です。
(1)
四角形ABCDの面積を求めなさい。
(2)
三角形AEFの面積を求めなさい。
(3)
三角形DGHの面積を求めなさい。
(4)
四角形ABCDと四角形IJKLの2つの四角形が重なる部分の図形の面積を求めなさい。
@解説@
(1)
本番では答案に考え方も書く。

正六角形の分割は中学受験で頻出なので慣れておこう。
上図のように6等分する。
1つの二等辺三角形は54÷6=9cm2
隣辺比から面積比は④:⑤、⑨=9cm2だから④=4cm2

今度は上図のように正六角形を6等分する。
外側延長で正三角形を作成。これは6等分した正三角形と合同で9cm2
同様に隣辺比から面積比は⑨:⑦で、⑨=9cm2だから⑦=7cm2
四角形ABCDの面積は正六角形から周りの4ヶ所を除外して、
54-(4+7)×2=32cm2
(2)
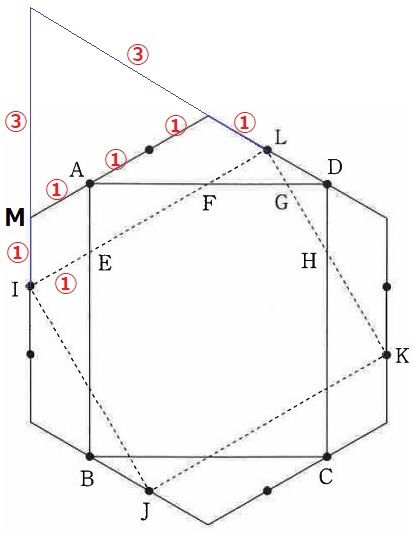
先ほどの外側延長で作った正三角形を利用する。
外にある正三角形の1辺を③とおく。
四角形AMIEに着目すると、2組の対辺が平行だから平行四辺形。
IE=MA=①

つづいて、NPに補助線をいれる。
四角形ABとNP、EとFは左右対称。(青線の台形を意識すると対称性が見えやすい)
四角形AMIEとNOLFは対称性から合同の平行四辺形である。
LF=IE=①
IL=④なので、EF=④-①-①=②
台形MILOの面積は、(1)で出した台形と同じ7cm2
上底と下底の比から△AEFの面積は、7×②/⑦=2cm2
(3)

外側延長で1辺③の正三角形を作成。AK=⑤
LDとAKは平行で、LD:AK=LG:GK=①:⑤

△QDRと△QLKの相似比は1:2
DR=⑥÷2=③
DHとRK、DRとHKは平行だから四角形DHKRは平行四辺形。
DR=HK=③
LG:GH:HK=①:②:③
二等辺三角形QLKは(1)で出した二等辺と同じ4cm2
面積比から四角形DLKRの面積は3cm2
上底と下底の比から△DGHの面積は、3×②/⑨=2/3cm2
(4)
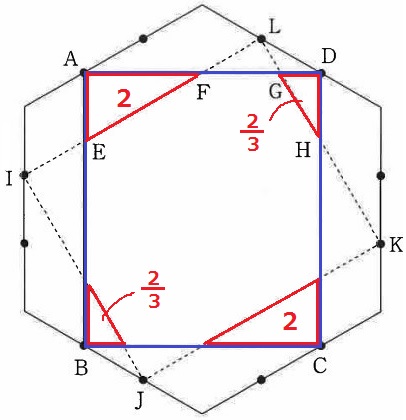
ここまで到達できたらサービス問題。
図形全体が点対称なので、下2つの三角形は△AEFと△DGHと合同である。
長方形ABCDから周りの4ヶ所を除外する。
32-(2+2/3)×2=80/3cm2



コメント