2021年度　大分県公立高校入試問題過去問【数学】解説

平均33.0点（前年比；＋1.1点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　97.9％
－２＋７＝５

②　89.1％
５－３²×２
＝５－18
＝－13

③　88.1％
３（ａ－２ｂ）－２（２ａ＋ｂ）
＝３ａ－６ｂ－４ａ－２ｂ
＝－ａ－８ｂ

④　82.9％
（ｘ＋２ｙ）/３＋（ｘ－ｙ）/５
＝｛５（ｘ＋２ｙ）＋３（ｘ－ｙ）｝/15
＝（８ｘ＋７ｙ）/15

⑤　83.6％
√18－４/√２
＝３√２－２√２
＝√２

（２）　73.7％
ｘ²－３ｘ－２＝０
解の公式を適用して。ｘ＝（３±√17）/２

（３）　76.9％
３ｘ＋２ａ＝５－ａｘにｘ＝２を代入。
６＋２ａ＝５－２ａ
４ａ＝－１
ａ＝－１/４

（４）　66.8％
全体は６×６＝36通り
積が９の倍数→３の素因数が２個必要→３か６を使う
（３、３）（３、６）（６、３）（６、６）の４通り。
確率は、４/36＝１/９

（５）　66.1％

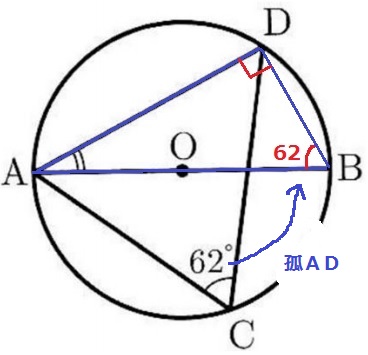
ＢＤに補助線。
孤ＡＤに対する円周角で、∠ＤＢＡ＝62°
半円の弧に対する円周角で、∠ＡＤＢ＝90°
△ＡＤＢの内角より、∠ＢＡＤ＝180－（90＋62）＝28°

（６）２点…48.3％、１点…25.2％
①『点Ａ、Ｂからの距離が等しい』
→ＡＢの垂直二等分線
②『半直線ＯＸ、ＯＹからの距離が等しい』
→∠ＸＯＹの二等分線
①、②の交点がＰである。

大問２（関数）

（１）　82.6％
ｙ＝ａｘ²にＡ（２、２）を放り込む。
２＝４ａ
ａ＝１/２

（２）　65.3％
ｙ＝１/２ｘ²にｘ＝－４を代入してＢ（－４、８）
Ｂ（－４、８）→Ａ（２、２）
右に６、下に６だから傾きは－１。
Ａから左に２、上に２移動して切片は４。
ｙ＝－ｘ＋４

（３）　7.7％!!

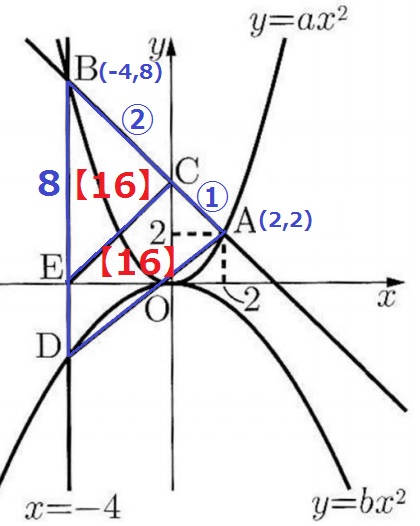
ｘ座標を手がかりに、ＢＣ：ＣＡ＝４：２＝②：①

面積比は隣辺比を用いる。
△ＢＣＥの面積比…８×②＝【16】
仮定より四角形ＡＣＥＤ＝【16】だから、△ＢＡＤの面積比は【32】。
ＢＤ×③＝【32】（*数字×〇＝【 】）
ＢＤ＝32/３
ＥＤ＝32/３－８＝８/３

Ｄ（－４、－８/３）をｙ＝ｂｘ²に代入。
－８/３＝16ｂ
ｂ＝－１/６

大問３（データの活用＆数量変化）

（１）①　66.6％
最頻値（モード）は最もあらわれている値。
９月は３本、11月は４本。
11月の方が大きい。

②記号…71.5％、理由２点…34.7％、１点…9.5％、無記入…12.9％
ア：最頻値を仮の平均として平均値を出してみる。
■９月の平均
３を仮の平均とすると、、
－２×１－１×３＋０×４＋１×１＋３×２＋４×１＝６
３＋６÷12＝3.5本
■11月の平均
４を仮の平均とすると、、
－４×１－２×２＋０×３＋１×２＋２×１＋４×１＝０
４本だから、11月の方が大きい。〇

イ：12人の中央値（メジアン）は６番目と７番目、10人の中央値は５番目と６番目の平均。
９月…３本、11月…４本で11月の方が大きい。〇

ウ：９月…３÷４＝0.25、11月…２÷10＝0.2
11月の方が小さい。×

エ：範囲（レンジ）＝最大値－最小値
９月…７－１＝６本、11月…８－０＝８本
11月の方が大きい。〇
答えはウ。適切でない理由は0.25＞0.2を指摘すればいい。

（２）①　46.3％

花子は２秒後に出発する。
傾きは３/４なので、右に４マス、上に３マス移動する。
格子点を意識して線を伸ばすと（18、12）でフィニッシュ。
ｙの最大値は12ｍなので延長しない！

②ア46.5％、イ２点…27.7％、１点…9.8％、無記入…34.1％

花子が12ｍに達したのは、太郎が出発してから18秒後。
このときのｙ座標の差を求めればいい。
ア…18
イ…ｘ＝18のときの互いのｙ座標の差

大問４（規則）

（１）　89.1％
題材が特殊である(´･∀･`)

３個ずつ増えている。
５番目は13個。
６番目は16個。

（２）３点…49.3％、２点…5.9％
【１、４、７、10、13、16…】
上の数列を一般化する。
初項１＋公差３×（ｎ－１）
＝３ｎ－２個

（３）　23.2％！
先の式を用いる。
３ｎ－２＝100
ｎ＝34

34番目の竹の本数を求める。
１番目の右上がりは２本、右下がりは２本。
34番目の右上がりは35本、右下がりは35本。
これに横の４本を足す。
35＋35＋４＝74本

大問５（空間図形）

（１）　48.3％
Ｐは底面の半径がｂ、高さ１の円錐。
ｂ×ｂ×π×１÷３＝１/３πｂ²ｃｍ³

（２）　27.1％！
Ｑは底面の半径が１、高さｂの円錐。
１×１×π×ｂ÷３＝１/３πｂｃｍ³

Ｑの体積÷Ｐの体積
＝１/３πｂ÷１/３πｂ²
＝１/ｂ倍

（３）　4.1％!!

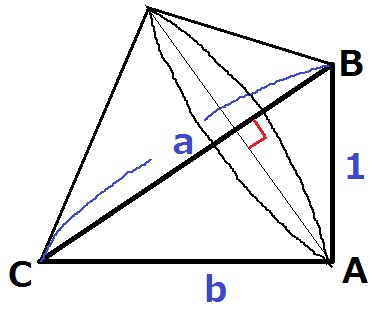
↑２つの円錐を合わせた立体になる。
回転体の半径が知りたい。

ＡからＢＣに垂線、交点をＤとする。
２角相等で△ＡＢＣ∽△ＤＢＡ（この直角三角形の相似形は頻出！）
ＤＡ＝ｂ×１/ａ＝ｂ/ａ
Ｒは底面の半径がｂ/ａ、高さの合計ａの円錐。
ｂ/ａ×ｂ/ａ×π×ａ÷３＝πｂ²/(３ａ)ｃｍ³

Ｒの体積÷Ｐの体積

１/ａ倍

（４）　13.5％！
今までのおさらい。

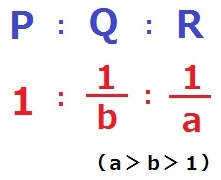
Ｐの体積を１とすると、（２）よりＱの体積は１/ｂ。
（３）よりＲの体積は１/ａ。
ａ＞ｂ＞１だから、１＞１/ｂ＞１/ａ。
（１を大きい数値ａで割るから、１/ａが最も小さい）
小さい順に並べると、Ｒ＜Ｑ＜Ｐ。

大問６（平面図形）

（１）３点…36.1％、２点…5.8％、１点…18.5％、無記入…19.9％
△ＡＢＣ∽△ＦＰＣの証明。

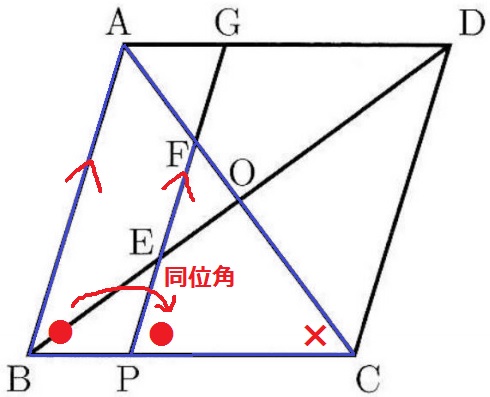
共通角（×）とＡＢ//ＦＰより同位角（●）→２角が等しく∽。

（２）①　46.9％
菱形だけで決着がつく。

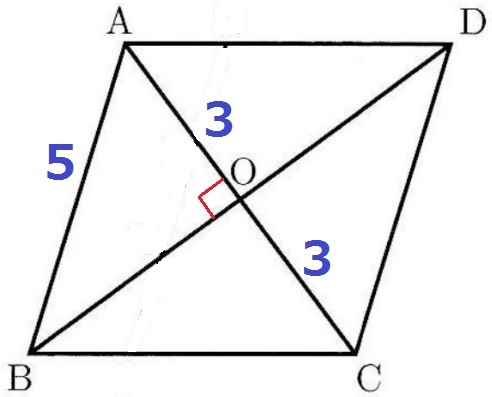
↑無駄な線を消去しました。
菱形の対角線は各々の中点で交わるから、ＡＯ＝３ｃｍ
また、対角線は直交するので、∠ＡＯＢ＝90°
△ＡＯＢは辺の比が３：４：５の直角三角形。
ＢＯ＝４ｃｍ

②　0.1％!!!
ムズイね:( ´ω` ):

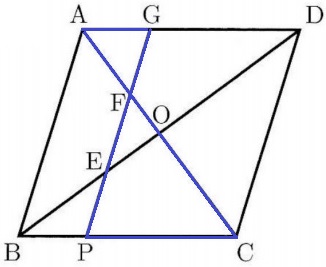
△ＡＦＧの面積が知りたい。
これと相似にあるのは△ＣＦＰ。
△ＣＦＰの面積はいくらだろう？

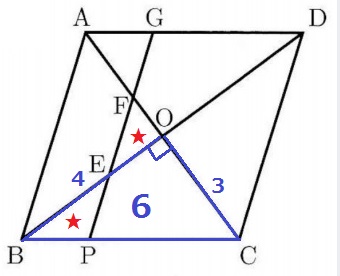
ここで与えられた『△ＢＰＥと△ＥＯＦの等積』を使う。
△ＯＢＣの面積はすぐ出せる。４×３÷２＝６ｃｍ²
四角形ＣＰＥＯ＋★＝６だから・・

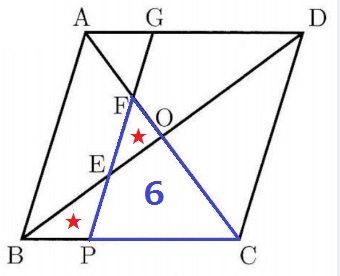
△ＣＰＦの面積は６ｃｍ²とわかる。
ＡＦ：ＦＣがわかれば、△ＡＦＧと△ＣＦＰの面積比が算出できる。

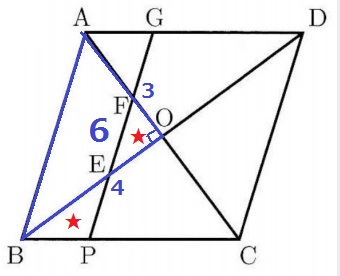
△ＡＯＢも６ｃｍ²。
四角形ＡＦＥＢ＋★＝６だから、、

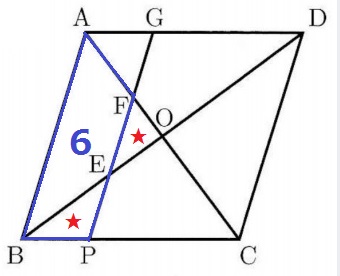
四角形ＡＦＰＢも６ｃｍ²です。

ＡＢ//ＦＰなので、△ＡＣＢ∽△ＦＣＰ。
面積比が△ＡＣＢ：△ＦＣＰ＝12：６＝２：１だから、
辺の比はＡＣ：ＦＣ＝〇√２：①
ＡＦ：ＦＣ＝〇√２－１：①

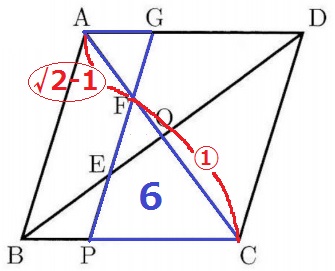
△ＡＦＧと△ＣＦＰの面積比は、
（√２－１）²：１²
＝３－２√２：１

△ＡＦＧの面積は、６×（３－２√２）＝18－12√２ｃｍ²