問題ＰＤＦ
月の満ち欠けや月食、日食を観察すると、月のことがいろいろとわかってきます。たとえば、日食のとき月の影の輪郭ははっきりして見えますが、月食のとき月に映った地球の影の輪郭はぼんやりして見えます。ここから、地球と月のある違いがわかります。
（１）
日食や月食の特徴として誤っているものはどれですか。
ア：日食は、明け方や夕方でも発生することがある。
イ：日食は、満月のときでも起こるときと起こらないときがある。
ウ：月食は、地球の影に月が入るため夜間に起こる。
エ：月食は、完全に離宮の影に入ると月が赤っぽく見える。
（２）
本文中の下線部について、「ある違い」とは何ですか。
地球と異なる月の特徴を10字以内で答えなさい。
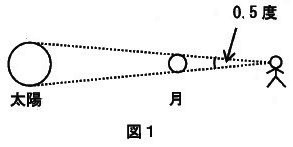
また、図１のように皆既日食の観察から、地球から見た月の大きさは、地球から見た太陽の大きさとほぼ等しく、視直径（見かけの直径）で0.5度程度なことがわかります。これは、腕をのばした先に見える（ Ａ ）の大きさになります。この結果は非常に有益で、地球に届く太陽光線は、平行線でないことを示しています。具体的にどのくらいの変化があるかというと、地球に届く太陽光線でつくられる影の大きさは、（ Ｂ ）くらいです。これらの結果から、月の大きさや地球から月までの距離を推測することができるのです。
（３）
（Ａ）に当てはまるものはどれですか。
ア：50円玉の穴くらい
イ：ブルーレイディスクやＤＶＤの穴くらい
ウ：ピンポン球くらい
エ：テニスボールくらい
（４）
（Ｂ）に当てはまるものはどれですか。
ア：地球－太陽間の距離で、およそ月１つ分小さくなる
イ：地球－月間の距離で、およそ月１つ分小さくなる
ウ：地球－太陽間の距離で、およそ月半分小さくなる
エ：地球－月間の距離で、およそ月半分小さくなる
図２は、1982年から2014年までの月食時の様子をまとめたもので、図３は、底辺が１ｋｍの直角三角形の高さと、斜辺と底辺の間の角度の関係をまとめたものです。
（５）
図２の暗い部分は地球の影です。
この図から、地球の影の直径は、月の直径の何倍ですか。整数で答えなさい。
（６）
地球の直径を12800ｋｍとすると、月の直径は何ｋｍですか。
（７）
地球から月までの距離は何万ｋｍですか。千の位を四捨五入して万ｋｍで答えなさい。
＠解説＠
（１）イ
日食は〔太陽〕－〔月〕－〔地球〕と、太陽と地球の間に月が入ることで起こる。
月が太陽の方向にあるので、地球の夜側は新月の状態。
ただ、明け方や夕方であれば太陽の方向を眺められるので、日食を観察できる。
（アは○、イは×）
月食は〔太陽〕－〔地球〕－〔月〕と、太陽と月の間に地球が入ることで起こる。
月が太陽の反対側にあるので、地球の夜側は満月の状態。（ウ○）
月食のとき、月が赤く見える原理は夕焼けが赤いのと同じ。
地平線上に太陽がくると光が地表に対して斜にあたるので、
太陽光が通過すべき大気の層が長くなる。
波長の短い青い光は大気とぶつかって散乱するが、
波長の長い赤い光は大気をすり抜けて地表に到達するので赤く見える。（エ○）
皆既月食の状態になると、地球の周りにある大気を通過した光が月に当たる。
青い光は散乱して、赤い光は屈折して月にあたるので月が赤く見える。
ストロベリームーンも同じ。
（２）月には大気がない。
月食時に地球の影の輪郭がボヤけて観察される理由。
ここまで問われるとはね(;`ω´)
先のとおり、月食時の月が赤くみえるのは太陽光が地球の大気を通過するため。
そのときの散乱で月食がぼんやりと見える。
対して、月には大気がないため、日食時の月の影の輪郭ははっきり見える。
（３）ア
知識問題。難しい。
視直径0.5度は、腕を伸ばした先に見える50円玉の穴の大きさ（穴の上下ぐらい）といわれる。
ゲンコツの幅が10度、小指の爪が１度くらい。
腕の長さを地球～月の距離に伸ばせば50円玉の穴は月と同じくらいに、
地球～太陽の距離に伸ばせば、穴は太陽と同じくらいの大きさになる。
（４）イ
リード文がわかりづらく書かれてある(;´Д｀)
地学では太陽が遠くにあることから、地表に降り注ぐ太陽光線を平行をみなすときがあるが、
もし、平行であれば〔太陽〕－〔月〕－〔地球〕と天体が並んだとき、
月と同じサイズの影が地球にできるはず。
しかし、実際は太陽光線は平行ではないので、月の影の大きさは小さくなる。
うえの本影のところが地球につくられる月の影にあたる。
本影のなかにいると、皆既日食が見られる（半影だと部分日食）。
本影は月の影なので、本影は月～地球間で小さくなっていくが、
月の影がどれほど小さくなるかで迷う(´ﾟдﾟ｀)
視直径が0.5度で、太陽と月の接線を通過するように線を描くと、
影のサイズは月の半分より小さくなるだろう、と推測するしかないような…？？
およそ月１つ分小さくなると月の影がほぼなくなることになるので選ぶのに勇気がいるが、
うえの写真のように、本影のエリアは非常に狭い。
地球は自転しているので、本影に入るエリアは地球上では帯状となる。
これを皆既帯といい、皆既帯の幅はムラがあるがだいたい数百キロほどで、
地球の直径12800ｋｍと比べると非常に限られた範囲となる。
（５）３倍
図２は月食時で、真ん中の黒い部分が地球の影、光っている多くの円が月。
目分量ではかる。地球の影の直径は、月の直径の３倍。
国立天文台より。地球は月よりも大きいので、月食の本影は日食のそれよりも大きい。
本影にある月は３つ分ほど。
（６）3200ｋｍ
（４）より、地球～月の距離で影の大きさは月１つ分小さくなる。
（５）の本影（地球の影）も同じ距離でできたものなので、地球より月１つ分小さくなっている。
よって、地球の直径は月の直径の４倍。
12800÷４＝3200ｋｍ
（７）37万ｋｍ
視直径から地球－月間の距離を求める。
ここも前問の答えを利用するので、どこかで間違えるとなだれ式で×になる…。
図３は、直角三角形の底辺を１ｋｍとしたとき、
高さと、斜辺と底辺の間の角度の関係を表したグラフ。
この角度が大きくなるほど、底辺からの距離（高さ）は長くなる。
直角三角形を作図。
前問より月の直径は3200ｋｍ、視直径は0.5度なので、
高さ1600ｋｍ、斜辺と底辺の間の角度は0.25度。
図３から、1.0度で0.0175ｋｍ。
0.25度では、0.0175÷４＝175/40000ｋｍ
１ｋｍ×1600 /（175/40000）
＝1600×40000÷175 ←25で約分
＝1600×1600÷７
＝2560000/７ｋｍ
＝256/７万ｋｍ
＝36.7…万ｋｍ ⇒37万ｋｍ
ケタ処理に苦労するが、知識で当ててしまった生徒はいたかもしれない。
図３は高１で習うタンジェント（ｔａｎ；正接、底辺と高さの比）。
タンジェントを知らない小学生でもグラフから読み取れば、
計算に必要な値が出せるように工夫されている。
難関中学（理科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント