問題PDF
白黒2種類のたくさんの積み木と1枚の板を用意した(図1)。
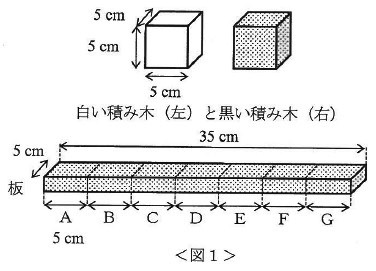
積み木は白黒とも1辺が5cmの立方体で重さは等しく、色だけ違う。
板は長さ35cmで、5cmごとに区切ったA~Gの積み木を積む場所がある。
まず、机の上に黒い積み木を1つ置き、Dが重なるように板をのせた(図2)。 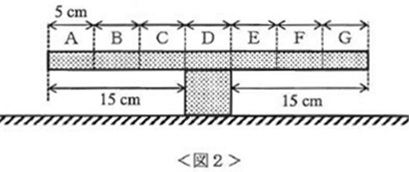
次に、この上にいろいろな積み方で積む木をのせて観察した。
以下の文の( ① )~( ⑦ )に当てはまる数値を答えなさい。
【操作1】
白い積み木を1つ使う。これをAに積むと、板の左はしが下がった。
Bに積むと水平のままだった。C~Gに順番に積んでみると、
C、D、E、Fでは板は水平のままだったが、Gでは右はしが下がった。
【操作2】
A~Gに黒い積み木を1つずつ、計7個積んだ状態を「土台1段」とする(図3左)。
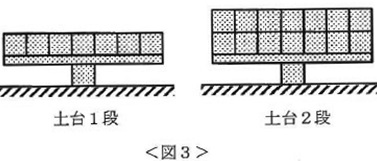
【操作1】と同じように、白い積み木を1つ積んでみたが、A~Gのどこでも板のはしが下がることはなかった。次に、白い積み木をAにだけ積み、その数を1個から2個、3個と増やしてみた。
すると、全部で( ① )個積んだときに、板の左はしが下がった。
今度は、A~Gに黒い積み木を2つずつ、計14個積んだ状態を「土台2段」とする(図3右)。
「土台1段」と同じように、Aに積む白い積み木の数を1個から2個、3個と増やしてみると、
全部で( ② )個積んだとき、板の左はしが下がった。
【操作3】
白い積み木をつかって、図4のような階段状の積み方を考える。
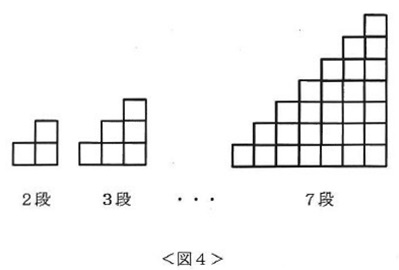
図4の左から「2段」、「3段」、・・「7段」となる。それぞれの「段」をその形のまま板の上に積んでみた。「2段」では、階段の左はしがA~Fになる6通りの積み方があるが、このうおち板のはしが下がらないのは2通りあった。「3段」では、5通りの積み方のうち、板のはしが下がらないのは( ③ )通りあった。「4段」では、4通りの積み方のうち、板のはしが下がらないのは( ④ )通りあった。「5段」では、3通りの積み方のうち、板のはしが下がらないのは1通りあった。「6段」では、2通りの積み方のうち、板のはしが下がらないのは1通りあった。「7段」では、1通りの積み方しかないが、これをのせると板のはしが下がった。
【操作4】
「7段」の下に黒い積み木で「土台1段」、「土台2段」、・・・のように、土台を1段ずつ追加してみた。すると、「土台( ⑤ )段」となったとき、板が水平のままとなった。同じように、「6段」では、「土台( ⑥ )段」となったとき、すべての積み方で板のはしが下がらなかった。また、「5段」では、「土台( ⑦ )段」となったとき、すべての積み方で板のはしが下がらなかった。
@解説@
最初でコケると雪崩式で全敗の危険があります。合否の分水嶺となった大問。
①3個 ②4個 ③2通り ④1通り ⑤4段 ⑥5段 ⑦5段
①最初で原理を掴まないと太刀打ちできない。
端以外の中5つでは水平だが、端に乗せたら下がった。
では、Bに1コ乗せたときになぜ下がらなかったのか。
板に注目!
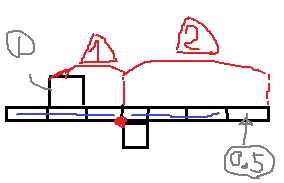
板を無視する問題も多いが、注意書きがないので板も考慮する。
左に積み木を乗せても板が耐えたのは、板にも重さがあり、右側でふんばったから。
左が落ちそうなので、一番下の積み木の左上(図の●)を支点にして考えると、
板の7目盛り分のうち、3つずつは左右で同じなので打ち消し(図の━)
残りは、左が積み木1コ、右が最もはなれた板の1目盛り分。
積む木の重さを①とおく。
支点からの距離1:2をもとに計算すると、板の1目盛り分は○0.5。つまり積み木半分の重さ。
厳密にいえば、積み木をAとBをまたぐように置けば、まだ板は水平をキープできるかもしれないが、問題文ではA~Gの7ヶ所しか積み木を置けないので、以下、板の1目盛り分は積む木1個の半分の重さを支えられると考える。

土台1段追加。
左が倒れそうなので、支点●は左。
支点を対象に左右で同じところを━で削除。
右のモーメントは、積み木○1.5個分で支点からの距離が4だから、
○1.5×4=6
左は支点からの距離が3なので、
6÷3=②
すなわち、左端Aに積み木を2個まで積むことができるので、3個目から倒れる。
②土台を2段にする。

手順は、
①左右のいずれが倒れるか見極める。
本問は左端に積む木を載せるので左に倒れやすい。
だから、支点の位置●は左側にセットする。
②支点を基準に、左右で同じところを相殺。
③残ったところをモーメント計算。
計算結果が、左>右だと倒れる。左<右だと板は水平を維持する。
10÷3=○3.333・・・
積み木3個までは耐えられる。4個乗せると板は傾く。
③今度は階段上の積み木を板に乗せる。
2段だと水平を維持する組み合わせが2通りあるらしい。。
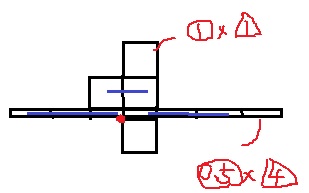
無難な乗せ方を考える。
最も数の多い列を真ん中(D)に乗せれば安定する。
左が落ちそうなので、支点を左にもってきて、左右で相殺。
モーメント処理をすると、右のモーメントが勝つ→板は水平。

先ほどの2段の積み木を左に1つ分ズラすと、3個の積み木が全部、支点の左にくるので倒れる。
右に1つ分ズラすと、左のモーメントが勝つので、板は水平を維持する。
では、3段ではどうか?
最も多いところを真ん中(D)にのせてみると、
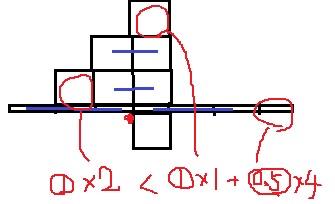
左に積み木が3つくるので、支点は左。
モーメントを計算すると右が勝つので板は水平。
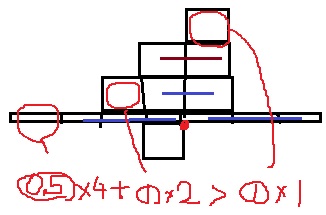
3段の6つの積み木を左に1つ分ズラすと、積み木6個が左に集中する。
だから、右にズラす。左に1つ、右に3つなので右が傾きそう→右に支点。
計算すると、左のモーメントが勝つので板は水平。
さらに左にズラすと、積み木5個がDより右にくるので右に傾く。
2通り
④4段を考える。
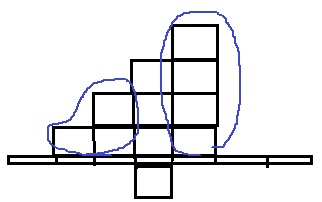
4つのところを真ん中(D)に乗せてしまうと、積み木6個が左に集中するので×。
3つのところを真ん中に乗せると、青のところが釣り合う。
(D列全てを支点と見たとき、左1に2つ+左2に1つ。Dから右1に4つだから)
この形を左右に1つ分ズラすと積み木の数がどっちかに偏って傾く。
1通り
⑤7段積む。
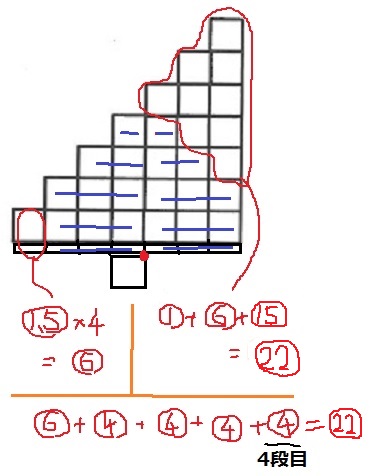
右に傾くので、右に支点をセット。左右で同じところを消す。
左⑥、右㉒
土台1段を追加すると、B~Gは相殺されるので、
Aのところの積み木1個分が左のモーメントに加算。
支点からの距離は4なので、モーメントが④ずつ追加。
⑥+④×4=㉒で、左右が釣り合う。
したがって、土台を4段追加すれば板は水平。
⑥6段バージョン。
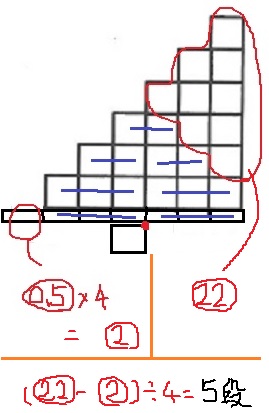
左のモーメント②、右はモーメント㉒。
土台1段で左に④のモーメントが追加なので、
(㉒-②)÷④=5段

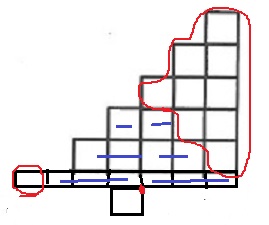

コメント