問題PDF
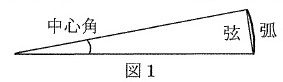
地球から見ると、月と太陽の大きさはほとんど同じに見えます。地球の直径は月の直径の4倍であり、中心角が小さいおうぎ形の弧の長さと弦の長さは等しいものとし(図1)、円周率は3.14として、以下の問いに答えなさい。
問1
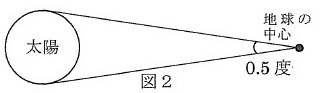
地球の中心から太陽を見たとすると、図2のように太陽の大きさ(角度)は0.5度に見えます。
地球の中心から太陽の中心までの距離は、太陽の大きさ(直径)の何倍になりますか。
小数第一位を四捨五入して答えなさい。
問2
地球の中心から月を見たとすると、月の大きさ(角度)も0.5度に見えます。
地球の中心から月の中心までの距離は、地球の大きさ(直径)の何倍になりますか。
小数第一位を四捨五入して答えなさい。
問3
地球の中心から月の中心までの距離は38万km、
地球の中心から太陽の中心までの距離は1億5000万kmです。
太陽の大きさ(直径)は月の大きさ(直径)の何倍になりますか。
小数第一位を四捨五入して答えなさい。
問4
地球の赤道上の地点で満月が頭の真上に見えたとき、
北極点や南極点ではこの月の中心を見ることができません。
では、北半球でこの月の中心が見える範囲は、北緯何度までですか。
図3を参考にして答えなさい。

@解説@
問1:115倍

地球の中心から太陽の中心までの距離を①とおく。
弦の長さは弧の長さと等しいとみなす→扇形の半径も①と考える。
太陽の直径は、半径①中心角0.5度の扇形の弧の長さに相当する。
太陽の直径…①×2×3.14×0.5/360=○157/18000
①÷○157/18000=18000/157=114.6…≒115倍
問2:29倍

地球の直径は月の直径の4倍。
地球からみて月の視直径(角の大きさ)が0.5度。
地球は月より4倍大きく、月-地球間の距離は月から見ても同じだから、
月からみた地球の視直径は0.5×4=2度と考えられる。
地球-月間の距離を①とおくと、地球の直径は①×2×3.14×2/360
前問の結果の4倍にあたる。
この値を逆数にした値が答えなので、前問の114.6…を÷4すればいい。
114.6…÷4=28.6…≒29倍
問3:395倍
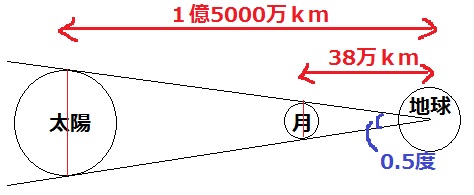
関係性を図示すると上図になる。
太陽の直径:月の直径=15000万km:38万km
15000万÷38万=394.7…≒395倍
問4:北緯89度
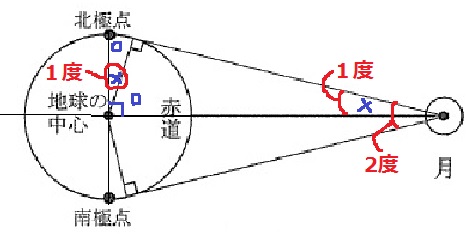
問2と同様に、月からみた地球の視直径を2度とする。
○+×=90°で等角を記す。
×=1度より、90-1=北緯89度


コメント