問題PDF
大きさが同じで、中まで白い立方体と中まで黒い立方体があります。これらを積み重ねて下の図のように大きな立方体を作りました。図の中の黒い部分は反対側の面まで黒い立方体だけが使われており、それ以外は白い立方体が使われています。このとき、次の問いに答えなさい。
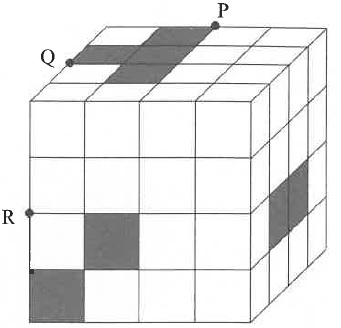
(1)
黒い立方体は全部で何個使われていますか。
(2)
図のような3点P、Q、Rを通る平面で大きな立方体を切断します。
このとき、上から1段目にある黒い立方体は何個切断されますか。
(3)
(2)の切断面において、白い部分と黒い部分の面積の比を
最も簡単な整数の比で表しなさい。
@解説@
(1)
上から1段ずつ調べるのが確実。

天井の4マスをすべて塗りつぶしたあとに、3段目の正面1マスと側面2マス、
4段目の正面1マスから1列すべてを追加で塗りつぶす。
計25個。
(2)
1段目に黒は4個ある。
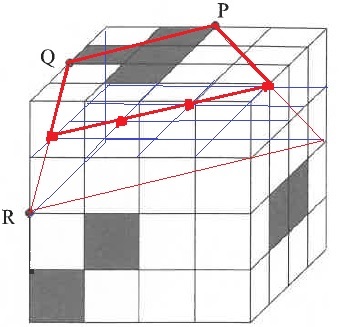
PQが切り込む。1段目の上面はPQ。
1段目の下面に注目!
下面の切断部分は、3×3の正方形の対角線にあたる。

↑上から見るとこんな感じ。
赤線は1段目の上面と下面が切断面と交わるところ。
この範囲にある立方体が切られる。
よって、3個。
(3)
立方体を中点で切断すると、断面に正三角形が登場する。
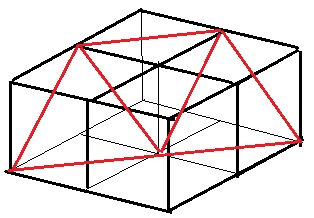
↑上向きと下向きが交互に現れる。
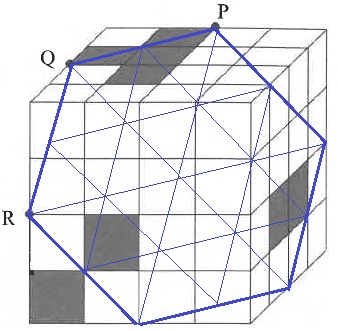
全体の切断面は正六角形で、各々の小さな立方体は正三角形に切られる。

(2)と同様に各段数の上面(切断の入り口)と下面(切断の出口)を赤線で表示する。
この範囲の中にある立方体が切断させる。
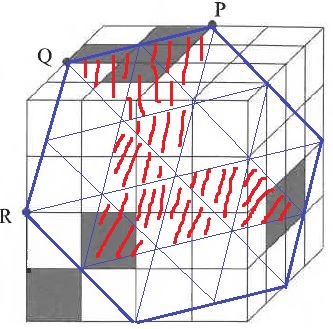
1段目は、上面の2つと、下面の真ん中1つが切られる。
2段目は、上面の真ん中1つと、下面の左から2つ目の1つが切られる。
3段目は、上面4つのうち真ん中2つ、下面は3つすべて。
4段目はゼロ。
白:黒=14:10=7:5



コメント