2018年度　ラ・サール中学過去問【算数】大問６解説

問題ＰＤＦ

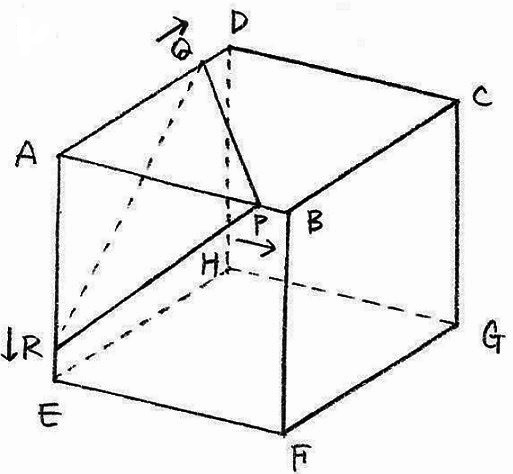
図のような立方体の頂点Ａから、３つの点Ｐ、Ｑ、Ｒが同時に出発し、ＰはＡ―Ｂ―Ｃ―Ｇ、ＱはＡ―Ｄ―Ｈ―Ｇ、ＲはＡ―Ｅ―Ｆ―Ｇの順に、それぞれ辺上を同じ一定の速さで移動して、12秒後に点Ｇに着きます。３点Ｐ、Ｑ、Ｒを通る平面でこの立方体を切ったときの切り口の面積をＳとするとき、出発して４秒後のＳは12ｃｍ²でした。このとき、次の場合のＳは何ｃｍ²ですか。

（１）出発して３秒後

（２）出発して６秒後

（３）出発して７秒後

を12秒で移動したということは、１辺を４秒で通過する。

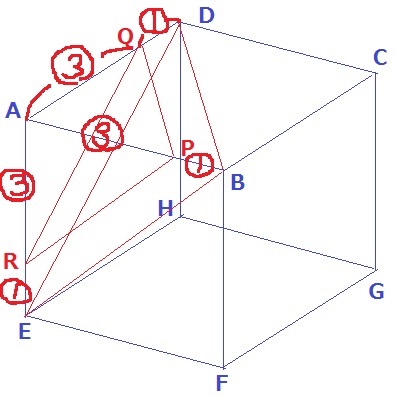
４秒後はＰはＢ、ＱはＤ、ＲはＥにあり、
４秒後の△ＰＱＲ12ｃｍ²は、正方形の対角線を１辺とする正三角形ＢＤＥとなる。

３秒度と４秒後はともに正三角形で相似。
面積比は辺の比の２乗。
12×（３×３）/（４×４）＝27/４ｃｍ²

（２）

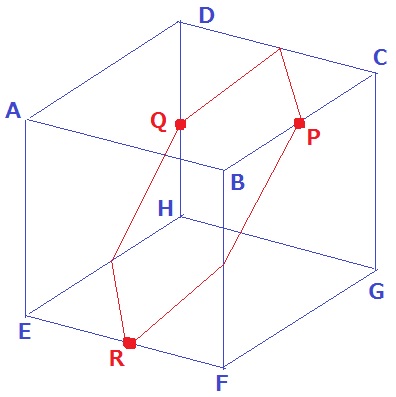
６秒後のＰ・Ｑ・Ｒは中点にくる。
断面は中学受験でお馴染みの正六角形となる。
手がかりは４秒後の正三角形ＢＤＥしかないので、
これに平行となるような正三角形を作図する。

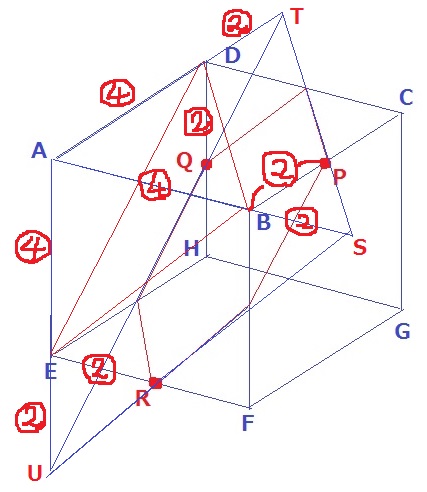
ＢＰ→ＢＳにもってくる。同様に、ＤＱ→ＤＴ、ＥＲ→ＥＵに移動。
正三角形ＳＴＵ＝12×（６×６/４×４）＝27ｃｍ²

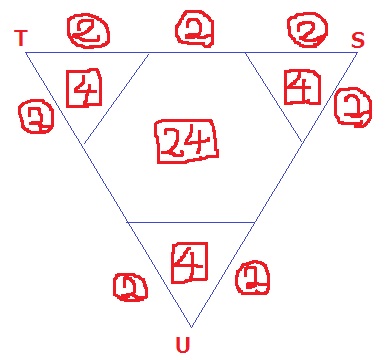
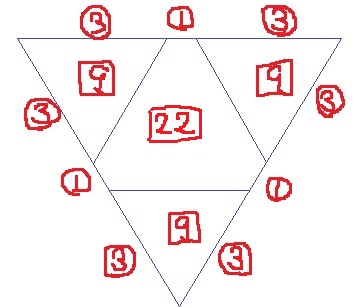
１辺⑥の正三角形から、１辺②の正三角形３つを引く。
中の面積比は、⑥×⑥－②×②×３＝〔24〕
27×〔24〕/〔36〕＝18ｃｍ²

（３）
前問と同様。
12×（７×７/４×４）＝147/４ｃｍ²

147/４×23/49＝33/２ｃｍ²
難関中（算数科）解 説ページに戻る