問題ＰＤＦ
１から300の数を１枚に１つずつ書いた、同じ大きさの正方形のカードがあります。
これら300枚のカードを、１のカードの右に２のカード、その下に３のカード、というように、
時計の針が進む方向にうずをまくようにして小さい順に並べていきます。
下の図は、カードを11枚並べ終えたときの様子を表したものです。
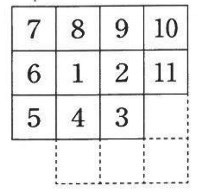
（１）
カードを25枚並べ終えたとき、25のカードと同じ縦の列および横の列に並んでいるカードは、
25のカードを含めてそれぞれ何枚ありますか。
（２）
カードを順に並べていくとき、100のカードのまわりはどのようなカードになりますか。
下の図のア、イ、ウに当てはまる数を答えなさい。
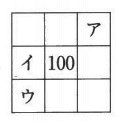
（３）
300枚のすべてのカードを並べ終えたとき、
300のカードと同じ縦の列および横の列に並んでいるカードについて、
それぞれ最も小さい数を答えなさい。
＠解説＠
（１）
はじめは取っ掛かりをつかむためにも、手を動かしてみる。
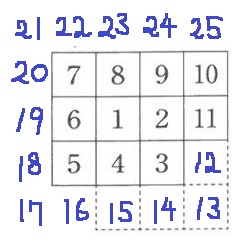
縦の列…５枚、横の列…５枚
（２）
偶数の平方数に着目する。
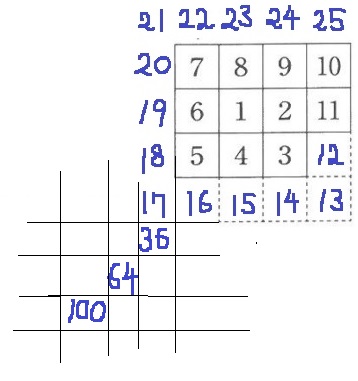
↑100はココ。
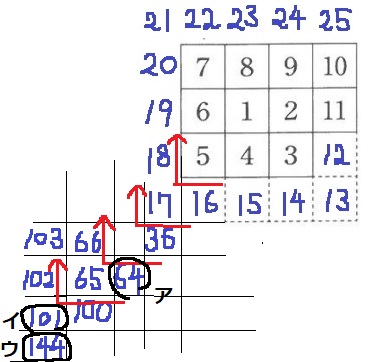
偶数の平方数の左隣をコーナーとして、数字が上にあがっていく。
ウは12×12＝144
ア…64、イ…101、ウ…144
（３）
300に近い平方数を考える。
17×17＝289、18×18＝326
300に近く、奇数の平方数はちょうど角にくるので、289から攻める。
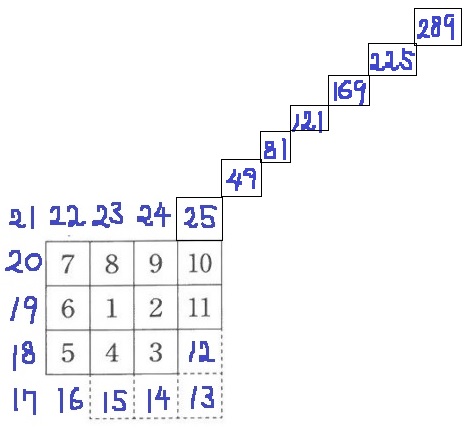
１を起点（１列目）とすると、289は１から右９列目、上９列目。
計算で出すと、（17－１）÷２＋１＝９
290は289の右隣にくる。
300まで降下すると、縦の列は290～300しかない。
縦の列の最小値→290
横は列の最小値→うえの図の通り、13。
グルグル数列は他の学校でも出題されています。
平方数の並びがポイントです。
難関中（算数科）解説ページに戻る
コメント