問題PDF
何枚かのオセロのコマ(片面が白、もう片面が黒のコマ)が白黒混ざった状態で円形に並べてあります。このコマに対して、以下の[作業]を、裏返すコマがなくなるまで繰り返します。
[作業]両隣の色が自身の色とは異なるコマをすべて選び、それらを同時に裏返す。
例えば、図1のようにコマが並んでいる場合、まず☆印のついた5つのコマを選び、裏返して図2のようにします。さらに、※印のついた1つのコマを選び、裏返して図3のようにします。図3には、両隣の色が自身の色とは異なるコマはないので、ここで[作業]の繰り返しは終了になります。

(1)
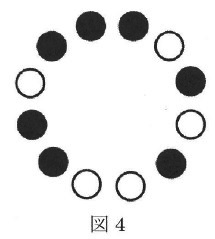
図4のように並んでいるコマに対して、裏返すコマがなくなるまで[作業]を繰り返したとき、最後まで1度も裏返されることのなかったコマをすべて選び、丸で囲みなさい。
(2)
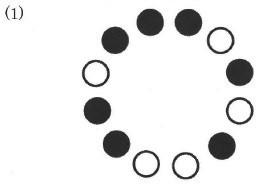
図5、図6のように並んでいるコマに対して、それぞれ裏返すコマがなくなるまで[作業]を繰り返したとき、最後の並び方はどうなりますか。解答欄の図に示しなさい。

(3)
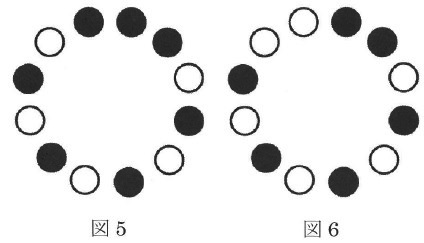
20枚のコマが図7のように並んでいます。これに対して、裏返すコマがなくなるまで[作業]を繰り返したとき、最後に黒は何枚になりますか。
(4)
31枚のコマを、白が16枚、黒が15枚になるように、好きな順番で円形に並べ、[作業]を繰り返します。最後に黒は何枚になりますか。最も多いときと最も少ないときの枚数を答えなさい。
@解説@
(1)
次の問題で作業終了時の並び方を求めるので、実際にやってみよう。
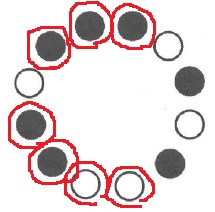
初期状態から1回目の作業で裏返さないコマが正解。
(2)
試行錯誤。白丸と黒丸を書くのが面倒なときは、A・Bにした方が早いかも。

図5は全部黒になります。

図6は左半分が白で、右半分が黒。
(3)

前問の結果を観察。

固まりがあるところは変わらない。
左は固まりが黒だけで、黒と白が交互になっているところがすべて黒になる。
右は固まりが黒と白で、交互のところが黒白で半分ずつ。
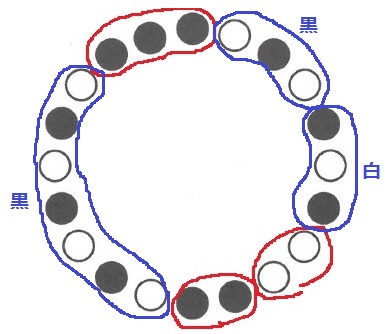
法則さえわかってしまえば、結果は予測できる。
固まりを探す。左の交互は黒に挟まれているからすべて黒。
右上側の交互は黒と白に挟まれているから、黒と白で半分ずつ。
白が5枚なので、黒は、20-5=15枚
(4)
白16枚、黒15枚、計31枚のコマがあり、
黒を最も多くする、もしくは最も少なくするにはどう配置すべきか。
■黒を最も少なくする。
白が黒より1枚多いので、図5と同じように○○の固まりを1つ作り、
残りを●○●○・・●と交互に配置すれば、すべて白になって黒が0枚となる。
■黒を最も多くする。
交互ゾーンをすべて黒に塗り替えたい。
そのためには交互ゾーンの両端は黒でなくてはならない。
しかし、黒1つだと塗り替えられてしまうので、●●と固まりにしておく。
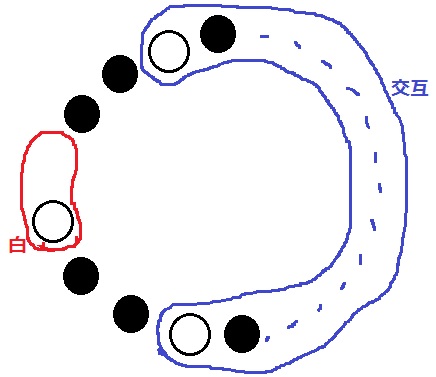
↑こんな感じ。
交互ゾーンは○●○●・・・・●○となる。
黒は固まりで4枚使ったので、交互ゾーンでは15-4=11枚。
交互ゾーンの白は、11+1=12枚。
左の赤いところで固まる白は、16-12=4枚
この白は作業後も白のままなので、作業後の黒の枚数は31-4=27枚
最も多いときの枚数・・・27枚、最も少ないときの枚数・・・0枚



コメント