問題PDF
図1のような平行四辺形ABCDの紙があります。
この紙を点Aと点Bがくっつくようにして、直方体の側面をつくります。
この直方体の底面は正方形で、直方体の体積は243/4cm3です。

(1)
図1のDEの長さを求めなさい。
(2)
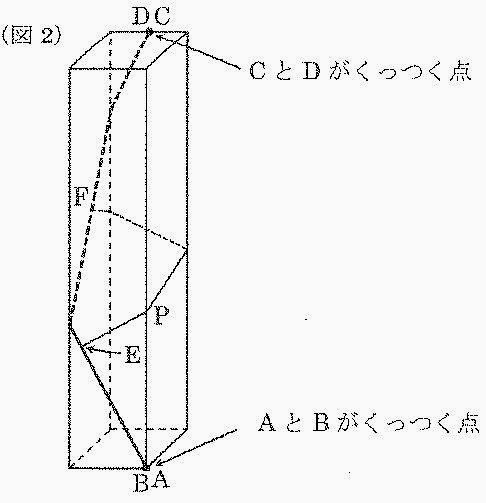
図2のように、点Aと点Bが直方体の頂点になるように側面をつくると、
図1のEとFを結んだ線は、直方体の辺の上にある点Pを通ります。
APの長さを求めなさい。
@解説@
(1)
そもそも平行四辺形で直方体の側面を作れるのだろうか?
隣同士の頂点をくっつけると、平行四辺形がグルっとまわって直方体の側面になる。
理由は隣同士の角の和が180°だからつなげると一直線になり、
平行四辺形の対辺は等しいのでピタッと接するから。
(試しに紙でやってみよう!円柱が作りやすいです)
平行四辺形は長方形が平行に傾いた四角形で長方形を巻けば柱となるから、平行四辺形も同様に柱を作れる。

AとBをくっつけると、AとBは底面の正方形の周りの長さになる。
この正方形の1辺は9÷4=9/4cm
底面積は、9/4×9/4=81/16cm2
直方体の高さは、243/4÷81/16=12cm
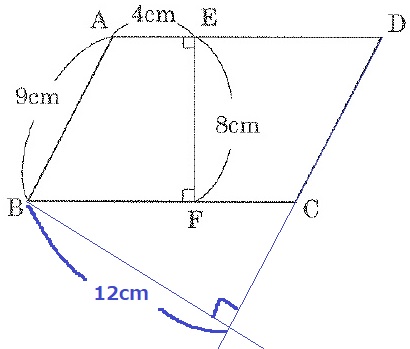
↑円柱の高さ12cmを展開図で示すとこうなる。
平行四辺形の面積からADの長さを求める。
AD=9×12÷8=27/2cm
よって、DE=27/2-4=19/2cm
(2)
PはAから伸びる垂線上にある。
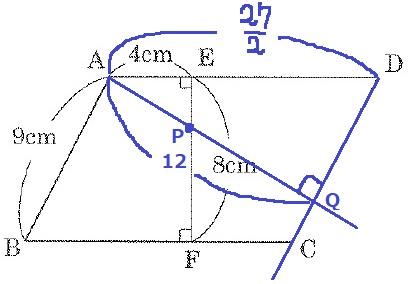
Aからおろした垂線とCDとの交点をQとする。
AQとEFとの交点をPとなる。
△APE∽△ADQより、AP:AE=AD:AQ
AP=27/2×4/12=9/2cm



コメント
はじめまして、小3男子です。
直方体の高さを求める時の256/4がよくわからないのでおしえてもらえますか?
れいさん
コメントありがとうございます。
通知が機能しておらず、だいぶ遅れてしまって申し訳ないです。。
問題文を確認したところ、243/4の誤りでした。訂正しておきますね。