2024年度　栄東中学・東大特待過去問【算数】大問１解説

問題ＰＤＦ
（１）
マヨネーズとケチャップを混ぜてつくったソースをオーロラソースといいます。東さんはマヨネーズとケチャップを３：１の割合で混ぜてつくったオーロラソースＡと、１：１の割合で混ぜてつくったオーロラソースＢをそれぞれビンに入れて冷蔵庫で保管していました。
　ある日、東さんはマヨネーズとケチャップを３：２の割合でつくるとおいしいと聞いたので、
ＡとＢを〔　　〕：〔　　〕の割合で混ぜることで、マヨネーズとケチャップの割合が３：２の
オーロラソースをつくりました。もっとも簡単な整数の比で答えなさい。

（２）
あるケーキ屋では、500円のケーキと300円のカヌレと100円のクッキーを販売しています。
ある日の売り上げは26200円で、カヌレはケーキより多く、ケーキはクッキーより多く売れました。
また、カヌレの売れた数はクッキーの売れた数の２倍より１個少ない個数でした。
カヌレは〔　　〕個売れました。

（３）
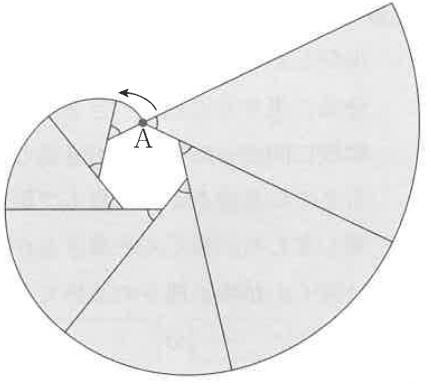
１辺の長さが１ｃｍの正七角形と、７ｃｍの長さの糸があります。
糸の端を点Ａに固定し、正七角形の周りに巻き付けました。
その糸をたるまないように図の位置までほどいたところ、糸が通った部分は、
影のついた部分になりました。その部分の面積は〔　　〕ｃｍ²です。

（４）
入学式の日に新入生を迎える教室をデコレーションするのに、栄くんと東さんの２人では30分、東さんと中さんの２人では40分かかります。ある教室で東さんが35分作業したところで、栄くんと中さんも加わって３人で作業をしたところ、その10分後に仕上がりました。栄くん、東さん、中さんの３人で最初から最後まで作業すると〔　　〕分かかります。

（５）
栄くんと東さんは同じ道を通って学校から駅まで歩きます。東さんが学校を出発した２分後に栄くんも歩いて駅に向かいました。栄くんは出発してから４分後に東さんに追いつきましたが、そこで忘れ物をしたことに気付き、すぐに学校に向かって走って引き返しました。栄くんが学校に着いてから再び出発するまでに３分かかり、走って駅に向かったところ、東さんより２分遅く駅に到着しました。栄くんと東さんが歩く速さはそれぞれ一定で、栄くんが走る速さは栄くんが歩く速さの２倍でした。東さんは学校を出発してから駅に到着するまでに〔　　〕分〔　　〕秒かかりました。

（６）
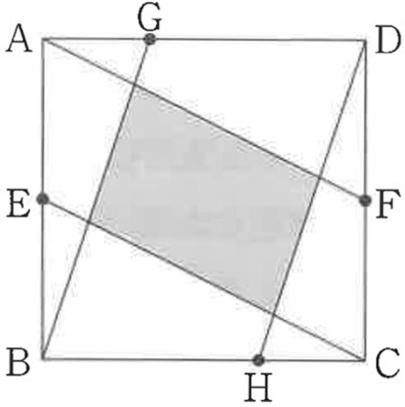
下の四角形ＡＢＣＤは正方形です。点Ｅと点Ｆはそれぞれ辺ＡＢ、辺ＣＤの真ん中の点で、
ＡＧ：ＧＤ＝１：２、ＢＨ：ＨＣ＝２：１です。
影のついた部分の面積は、正方形の面積の〔　　〕倍です。

＠解説＠
（１）

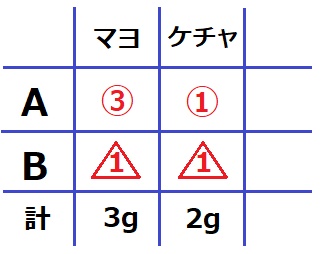
Ａのマヨ：ケチャ＝③：①
Ｂのマヨ：ケチャ＝△１：△１
ＡとＢを合わせたらマヨ＝３ｇ、ケチャ＝２ｇになったとする。

消去算。
　 ③＋△１＝３
－)①＋△１＝２
　②　　　＝１
①＝0.5
③＝1.5、△１＝２－0.5＝1.5ｇ

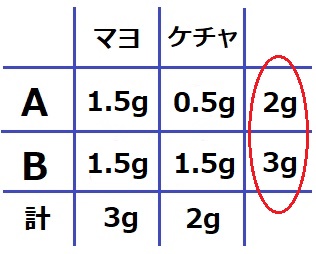
Ａを２ｇ、Ｂを３ｇ混ぜればよい。
Ａ：Ｂ＝２：３

（２）
情報整理。
ケーキ…500円、カヌレ…300円、クッキー…100円、売り上げ…26200円
販売個数はカヌレ＞ケーキ＞クッキーで、カヌレはクッキーの２倍より１個少ない。
『１個少ない』が気持ち悪いので、もう１個カヌレが売れたとする。
売り上げは、26200＋300＝26500円

クッキーを〇個とすると、カヌレは２倍で〇〇個。
【カヌレ×２＋クッキー】をセットでまとめる。
→セット料金は300×２＋100＝700円、セットの個数はクッキーと同じ〇個。
ケーキを△個で表すと、

700×〇＋500×△＝26500　←÷100
７×〇＋５×△＝265
カヌレ（〇〇）＞ケーキ（△）＞クッキー（〇）

265の一の位５から〇は５の倍数である。
〇＝５のとき、△＝（265－７×５）÷５＝46
（〇、△）＝（５、46）
７と５は互いに素→〇＝５と△＝７の交換で等式が維持されるのでどんどん交換していくと、
（〇、△）＝（５、46）（10、39）（15、32）（20、25）（25、18）…
条件より、△は〇より大きく、〇〇より少ないので、（〇、△）＝（20、25）しかない！
求めたいカヌレは〇〇個で、実際は仮定より１個少ないから、20×２－１＝39個

（３）

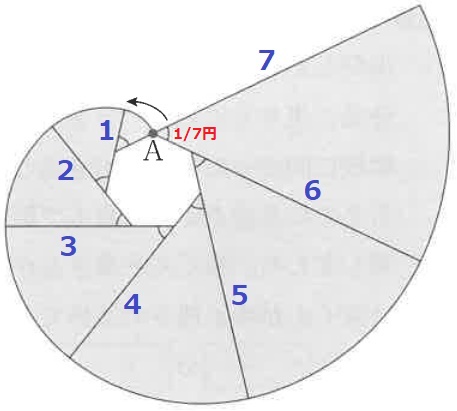
多角形の外角の和は360°。
正七角形だから、１つの外角はいずれも360/７°で等しい。
中心角360°は円→中心角360/７°は１/７円である。
面積は、（１×１＋２×２＋３×３＋４×４＋５×５＋６×６＋７×７）×3.14÷７
＝140×3.14÷７
＝20×3.14＝62.8ｃｍ²

（４）

１分あたりの仕事量は、
栄＋東＝１/30
中＋東＝１/40
個別の仕事量がわからない。。

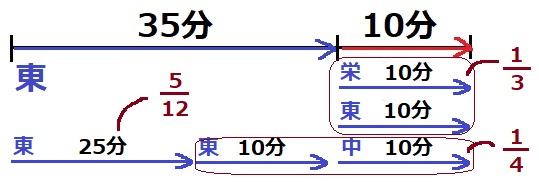
そこで、３人の10分を個別に分割する。
栄＋東の10分は、１/30×10＝１/３
前半の東35分から10分を持ってきて、中10分とくっつける。
中＋東の10分は、１/40×10＝１/４
東25分の仕事量は、１－（１/３＋１/４）＝５/12
１分あたりの東は、５/12÷25＝１/60

１分あたりの栄…１/30－１/60＝１/60
１分あたりの３人…１/60＋１/40＝１/24
３人でかかる時間は、１÷１/24＝24分

（５）

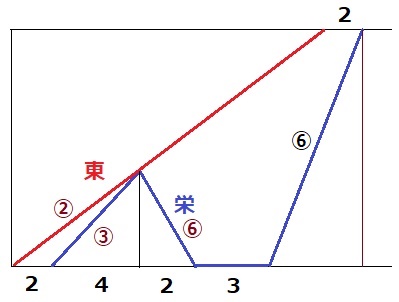
ダイヤグラムで整理する。
栄が東に追いつく地点まで、時間の比は東：栄＝６分：４分＝３：２
速さは逆比で、東：栄（歩）＝②：③
その後、栄は２倍速で走る→栄（走）＝⑥
栄が学校まで戻る時間は、４×３/６＝２分

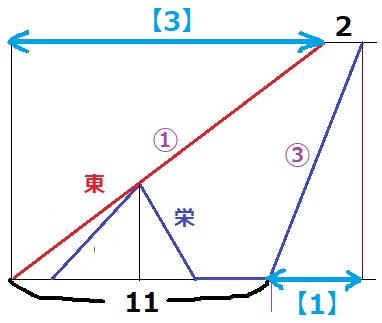
栄が東に追いついた地点の距離は不明。
距離一定が使えるのは学校～駅なので、全体の時間に着目する。
速さの比→東：栄（走）＝①：③
時間の比は逆比。東の時間を【３】とすると、栄のラストスパートは【１】。
【３】＋２＝11＋【１】
【２】＝９
求めたいのは東の【３】だから、９×３/２＝13.5分＝13分30秒

（６）
問題集によく掲載される典型題。

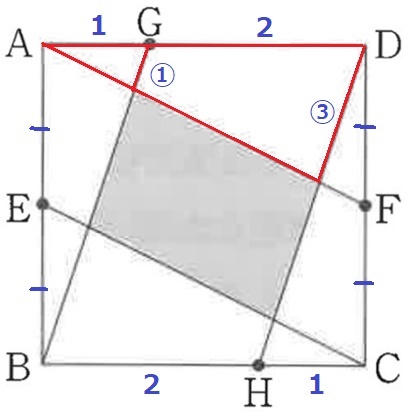
勾配が等しく、ＢＧとＨＤは平行。
赤線の三角形に着目して、辺の比は①：③。

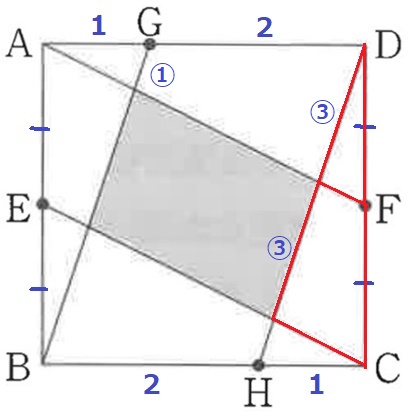
同様にＡＦとＥＣも平行。
赤線の三角形で、辺の比は③で等しい。

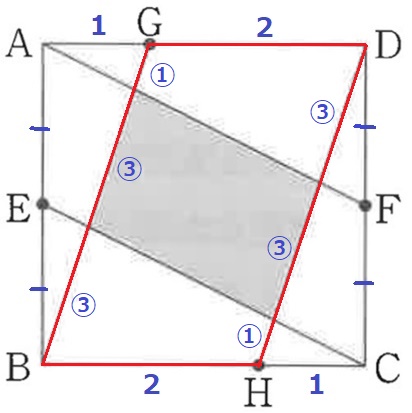
図形全体が点対称なので、下にも③、①がある。
正方形の面積を１とすると、ＢＨ：ＨＣ＝２：１より平方四辺形ＧＢＨＤは２/３。
ＢＧとＨＤが平行だから、上底と下底の和が使える。
斜線部分の面積比は、２/３×（③×２）/（⑦×２）＝２/７
正方形の２/７倍。
難関中（算数科）解説ページに戻る