問題ＰＤＦ
点Ａを中心とする半径が２ｃｍで中心角が270°のおうぎ形と、点Ｂを中心とする半径が２ｃｍで中心角が270°のおうぎ形があります。半径ＡＣと半径ＢＣが一つの直線になるように、２つのおうぎ形を点Ｃでくっつけた図形Ｆを作りました。
次の問いに答えなさい。ただし、円周率は3.14とします。また、（２）と（３）は答えを求めるのに必要な式をかき、それぞれの式が図のどの部分のものなのかわかるようにしなさい。
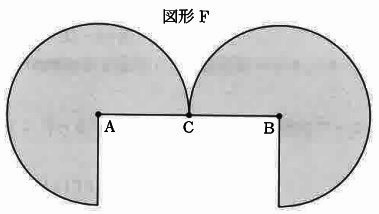
（１）
図形Ｆの面積は何ｃｍ2ですか。
（２）
点Ａを中心に図形Ｆを時計回りに90°回転させました。
図形Ｆが通ったあとにできる図形を解答らんの図を使ってかきなさい。
またその図形の面積は何ｃｍ2ですか。
（３）
点Ｃを中心に図形Ｆを時計回りに90°回転させました。
図形Ｆが通ったあとにできる図形を解答らんの図を使ってかきなさい。
またその図形の面積は何ｃｍ2ですか。
↑解答らん
＠解説＠
サクズ(乂’ω’) イノチ└(‘ω’)┘
（１）
２×２×3.14×３/４×２＝18.84ｃｍ2
（２）
図がきれいに書けないとミスります。
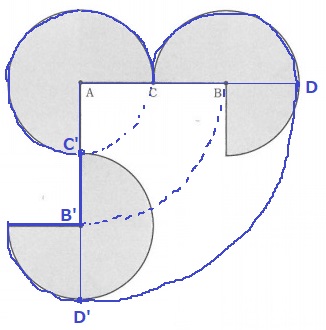
Ａを中心として時計回りに90°回転。
ＣをＣ’に、ＢをＢ’に移動。その延長にあるＤをＤ’に移動。
求積すべきところは青い線で囲ったところになる。
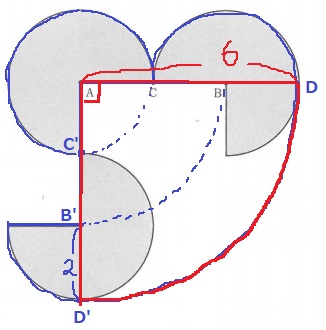
半径６の４分の１円＋半径２の円の1.5倍。
６×６×3.14×１/４＋２×２×3.14×３/２
＝47.1ｃｍ2
記述する際は、どの式がどこの面積にあたるかを示すこと。
（３）
Ｃを中心に時計回りに90°回転。
Ａ・Ｂ→直線部分の移動を先に決めてしまうのが良いかも。
青い線で囲ったところを求める。
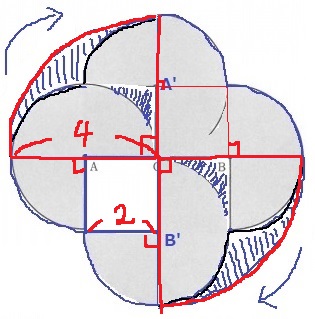
左下に正方形の空洞ができる。
４×４×3.14×１/２＋２×２×3.14＋２×２
＝41.68ｃｍ2
作図も能力の１つ。
いい加減な性格だとキツイ(;´Д｀)
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント