問題PDF
(1)
次の式の□にあてはまる数を求めなさい。

(2)
3つの整数800、1376、2144があります。
これらの整数をそれぞれ整数Nで割ったあまりはすべて等しくなり、
また3つの整数800、1376、2144の和はNで割り切れます。
このような整数Nのうち最も大きいものを求めなさい。
(3)
図のように、1辺の長さが2cmの立方体ABCD-EFGHがあり、EFの真ん中の点をM、EHの真ん中の点をNとします。また、AB上を秒速2cmで動く点Pと、AD上を秒速1cmで動く点Qがあり、どちらも頂点Aを同時に出発し、点PはAとBの間を、点QはAとDの間をそれぞれくり返し往復するものとします。P、QがAを出発してから2.5秒後の、四角形APME、四角形AQNE、三角形APQ、三角形EMN、三角形PMN、三角形PQNの6つの面で囲まれた立体の体積を求めなさい。
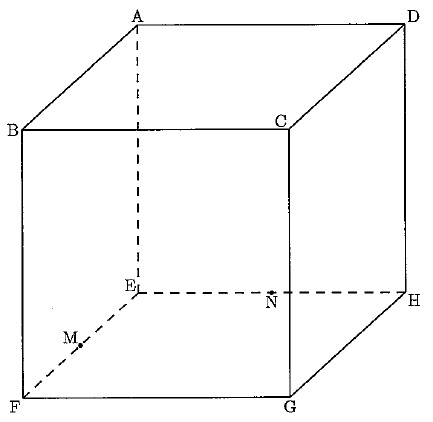
@解説@
(1)

なんじゃこりゅあー!((゚゚дд゚゚ ))
サボが受験生だったら速攻で捨てにいきます。
分母の数字がABABの並びだから101の倍数。

↑この□にあてはまる数の101倍が答え。

とりあえず、両辺を101倍して消してみた。
ここから手詰まる(;`ω´)
下手に計算するとカッコ内が負の数になるので、なるべく計算を回避したい。
左辺のカッコにあるそれぞれの数字を×51/70して、右辺のカッコにつなげる。
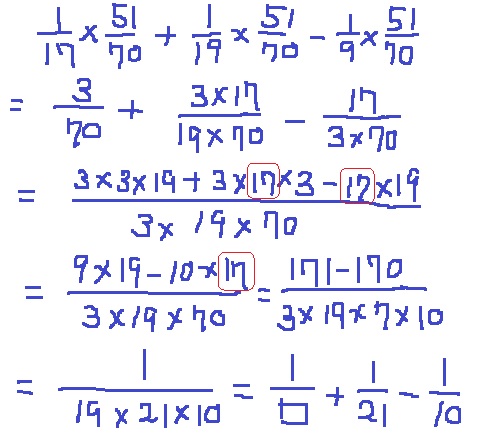
途中で分配法則を適用しています。
最後の分母は左辺の21と10に合わせて変形。
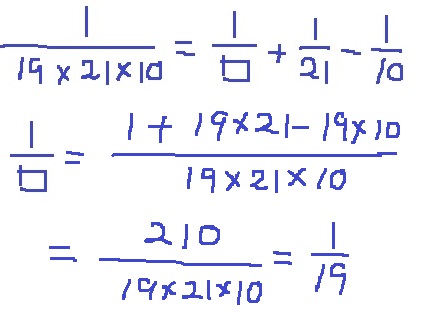
□=19
したがって、これを101倍した1919が答えとなる。
*最初、部分分数分解かな?と思ったのですが…サボの処理能力の限界です。
別解を見いだせた方は、お問い合わせよりお知らせ願います。
@@
算数大好きさん(@kimagure_mana)より素敵な解法を頂きました。
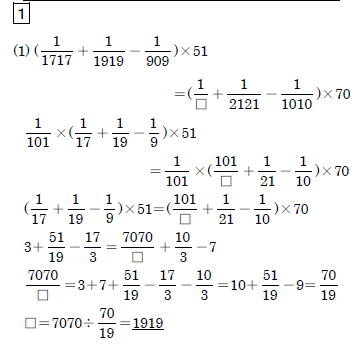
こちらの方が数字がスッキリしております。
サボはどうしてややこしく解いたのか、理解に苦しみますね(‘ω’)w
(2)
余りが等しいということは、各々の差が何かで割り切れる。
1376-800=576
2144-800=1344
2144-1376=768
576・768・1344の最大公約数をがんばって求める。
→192=2×2×2×2×2×2×3
一方で、800+1376+2144=4320
4320を素因数分解→2×2×2×2×2×3×3×5
共通因数は、2×2×2×2×2×3=96
よって、96が答え。
(3)
やけに問題文が長く、動点をからませている。
2.5秒後のPとQの位置を的確に定めよう。
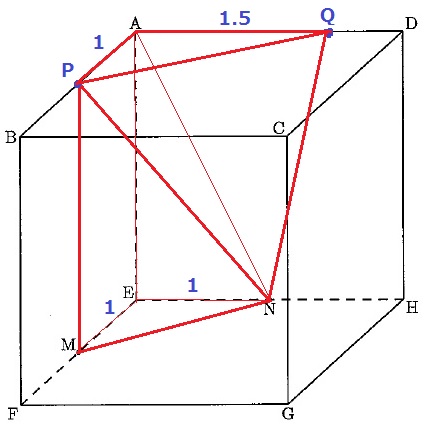
2.5秒間にPは5cm、Qは2.5cm動き、うえの位置にくる。
三角錐N-APQと四角錘N-APMEに分ける。
1×1.5÷2×2÷3+1×2×1÷3
=7/6cm3



コメント