問題ＰＤＦ
ウサギとカメが山のふもとから頂上まで競争をします。２匹は同時に一定の速さで走り始めましたが、走り始めて２分後にウサギが昼寝を始めてしまい、その48分後にカメが昼寝をしているウサギを追いこしました。
（１）
ウサギとカメの走る速さの比を、もっとも簡単な整数の比で答えなさい。
しばらくしてウサギが起きました。そのあと、もしウサギがもとの２倍の速さで走れば、３分後にＡ地点でカメに追いつき、カメより１分24秒早く頂上に着くことができます。
（２）
ウサギが昼寝をしていたのは何分間ですか。
（３）
ふもとからＡ地点までと、Ａ地点から頂上までの道のりの比を、
もっとも簡単な整数の比で答えなさい。
ところが実際には、ウサギは1.2倍の速さで走ったので、カメが頂上に着いたとき、
ウサギは頂上から260ｍ手前のところにいました。
（４）
山のふもとから頂上までの道のりは何ｍですか。
＠解説＠
（１）
山のふもとからウサギが寝た場所まで、ウサギは２分、カメは50分で着くので、
速さの比は、ウサギ：カメ＝50：２＝25：１
（２）
１分間にカメが歩く距離を【１】、ウサギが走る距離を【25】とする。
ウサギは昼寝ポイントまで２分で走るので、ふもとから【50】のところで寝た。
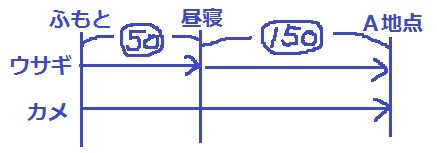
ウサギは起きてから２倍速の【50】で３分走り、Ａ地点でカメに追いつく。
昼寝～Ａ地点までの距離：【50】×３＝【150】
ふもと～Ａ地点までの距離は【200】で、カメは１分に【１】歩くから、
カメはふもとからＡ地点まで200分歩いたことになる。
ウサギが走った時間の合計は５分なので、寝ていた時間は195分間。
（３）
Ａ地点からウサギは【50】、カメは【１】の速さで走る。
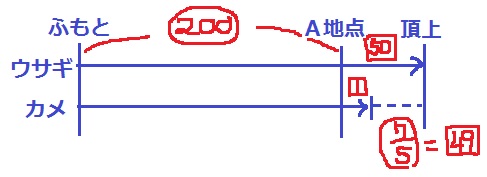
ウサギが頂上に到着してから、１分24秒＝７/５分後にカメが頂上に着く。
カメは１分【１】歩くので距離は【７/５】となり、これが□49に相当する。
Ａ地点～頂上：□50＝７/５×50/49＝【10/７】
ふもと～Ａ地点：Ａ地点～頂上＝【200】：【10/７】＝140：１
（４）
前問の図より、ふもと～頂上までの距離は、【200】＋【10/７】＝【1410/７】
カメは1410/７分間歩き、ウサギは目覚めてから、1410/７－２－195＝31/７分走る。
ウサギは起床後、１分に【25】×1.2＝【30】の速さで走るので、
ウサギが走った距離の合計は、【50】＋【30】×31/７分＝【1280/７】
カメが到着したとき、ウサギの残りの距離は【1410/７】－【1280/７】＝【130/７】
これが260ｍにあたる。
260ｍ×【1410/７】/【130/７】＝2820ｍ
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント