問題ＰＤＦ
白玉１個と黒玉がたくさんあります。
玉を入れることのできる一辺の長さが１ｃｍの立方体もたくさんあります。
立方体を何個か使って立体を作り、次のルールにしたがって玉を移動させます。
＠ルール＠
・１つの立方体には１個の玉しか入らない。
・空の立方体に、となり合う立方体から玉を移動できる。
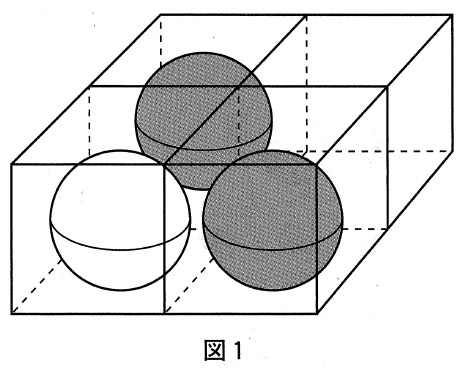
たとえば、立方体を４個使って、縦２ｃｍ、横２ｃｍ、高さ１ｃｍの直方体を作り、
図１のように白玉は１個、黒玉を２個入れます。
このとき、白玉を空の立方体の位置まで移動させる最も少ない回数は図２のように５回です。
ただし、図２は立体を上から見たときの図です。
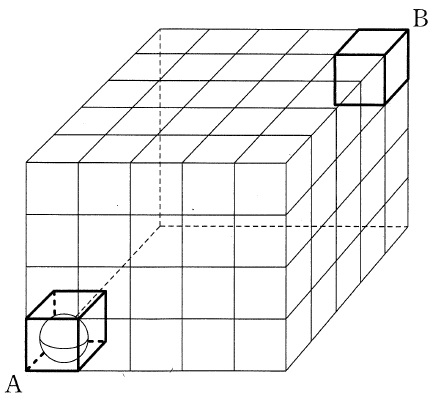
次の各立体において、頂点Ａをふくむ立方体に白玉を入れ、
頂点Ｂをふくむ立方体を空にし、残りの立方体に黒玉を入れます。
白玉を空の立方体の位置まで移動させる最も少ない回数を求めなさい。
ただし、以降の図は白玉のみをかいています。
（１）
立方体を８個使った、一辺の長さが２ｃｍの立方体
（２）
立方体を27個使った、一辺の長さが３ｃｍの立方体
（３）
立方体を100個使った、縦５ｃｍ、横５ｃｍ、高さ４ｃｍの直方体
＠解説＠
（１）
白玉の右上にある黒玉を、Ｂの空へ移動させる。
（言い換えれば、空箱を手前に移動させる）
立方体の正面４つの箱をみたとき、右の図のように左下が白玉、右上が空の状態となる。
図２から、左下の白玉を右上に移動させるには５回を要する。
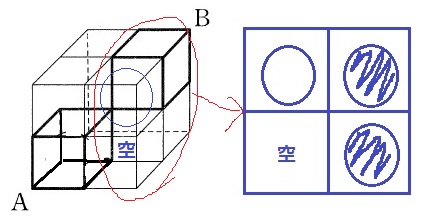
白玉を移動させたあとに、今度は側面の４つをみる。
黒→黒→白と３回移動させれば、白玉が右側（Ｂ）にくる。
よって、１＋５＋３＝９回
（２）
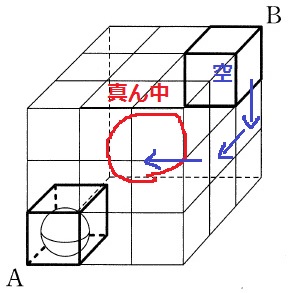
黒玉を３回移動させて、立方体の真ん中に空の箱を移動。
立方体全体で左下８つの箱は（１）の２×２×２と同じ形になるので、
Ａから真ん中に白玉を移動させるには９回。
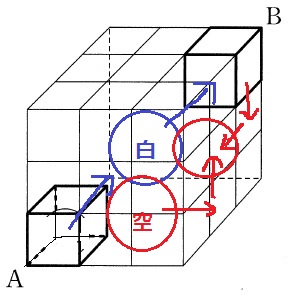
真ん中にある白玉をＢへ移動させる。
そのためには、白玉がある箱のＢに近い隣の箱へ空を移動させなくてはならないが、
Ｂに空があったときと同じ２回の移動なので、
つまるところ、白玉を斜め奥移動させるには９回の移動を要する。
３＋９＋９＝21回
（３）
前問までに動かす回数を分析しておくと楽になる。
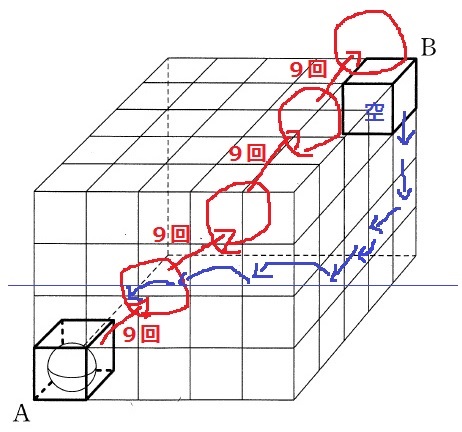
空の箱をＡの右上奥まで移動（８回；外側の正方形の辺の数を数えよう！）。
Ａにある白玉を斜め右上奥へ４度移動（９×４＝36回）。
Ｂの上に白玉、その下に空の箱の状態から、白玉をＢに戻すのに３回。
８＋36－３＝41回
難関中（算数科）解説ページに戻る
コメント