問題ＰＤＦ
１から９までの数字が書かれたカードがそれぞれ１枚ずつ、全部で９枚あり、
２つの空の袋Ａ、Ｂがあります。
（１）
はじめに、９枚のカードから１枚のカードを選び、袋Ａに入れます。次に、残ったカードから３枚のカードを選び、袋Ｂに入れます。袋Ａ、Ｂからカードをそれぞれ１枚ずつ取り出すとき、どのカードを取り出しても、取り出した２枚のカードに書かれている数の積が10の倍数となるような、袋Ａ、Ｂに入れるカードの入れ方は、何通り考えられますか。
（２）
はじめに、９枚のカードから１枚以上４枚以下の好きな枚数のカードを選び、袋Ａに入れます。次に、残ったカードから１枚以上４枚以下の好きな枚数のカードを選び、袋Ｂに入れます。袋Ａ、Ｂからカードをそれぞれ１枚ずつ取り出すとき、どのカードを取り出しても、取り出した２枚のカードに書かれている数の積が10の倍数となるような、袋Ａ、Ｂに入れるカードの入れ方は、何通り考えられますか。
（３）
はじめに、９枚のカードから１枚以上３枚以下の好きな枚数のカードを選び、袋Ａに入れます。次に、残ったカードから１枚以上３枚以下の好きな枚数のカードを選び、袋Ｂに入れます。袋Ａ、Ｂからカードをそれぞれ１枚ずつ取り出すとき、どのカードを取り出しても、袋Ａから取り出したカードに書かれている数が、袋Ｂから取り出したカードに書かれている数より６以上大きくなるような、袋Ａ、Ｂに入れるカードの入れ方は、何通り考えられますか。
＠解説＠
（１）
１～９の数のうち、必ず積が10の倍数となる組み合わせ→５×〔偶数〕
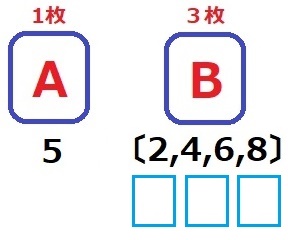
１枚のＡに５を入れる。
３枚のＢに偶数を入れる。
４つの偶数から３つを選ぶ→選ばれない１つを選ぶ→４Ｃ１＝４通り
（２）
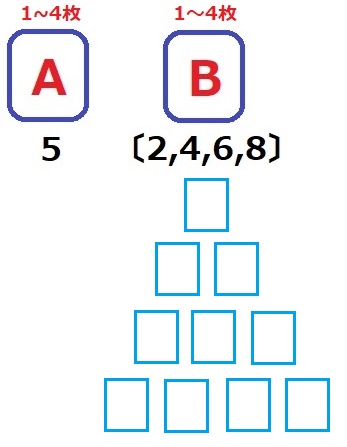
積が10の倍数となるには、必ず５を取らなければならない。
→片方の袋には５しか入れない。
Ａに５を入れ、Ｂに偶数を入れる。Ｂの枚数で場合分け。
１枚→４通り
２枚→４Ｃ２＝６通り
３枚→（選ばれない１枚を選ぶ）→４通り
４枚→１通り
４＋６＋４＋１＝15通り
ＡとＢを入れ替え、Ａに偶数、Ｂに５を入れるパターンを含めると、
15×２＝30通り
（３）
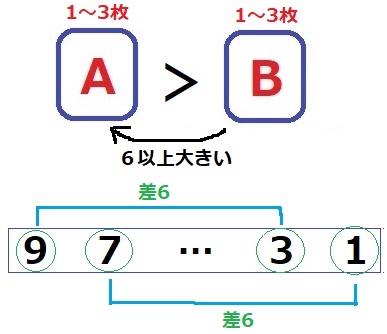
ＡがＢより６以上大きくなる。
差が６となる（９～３）（７～１）の組み合わせを意識する。
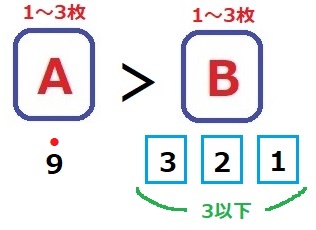
Ａに９だけを入れる⇒Ｂは３以下になればいい。
３枚のカードそれぞれを入れるか入れないかで、２×２×２＝８通り
全部入れないとＢに何も無くなるので、８－１＝７通り
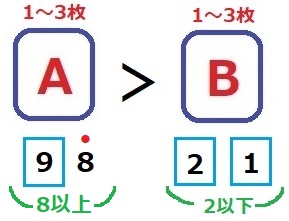
Ａに８を入れる⇒Ｂは２以下。
Ｂの組み合わせは、２×２－１＝３通り
Ａ側で９を入れるか否かで２通りあるから、３×２＝６通り
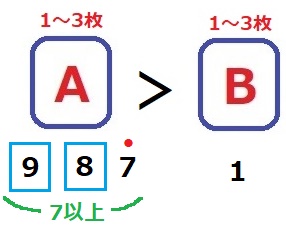
Ａに７を入れる⇒Ｂは１だけ。
Ａ側で９と８を入れるか否かで、２×２＝４通り
合計すると、７＋６＋４＝17通り
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント