問題ＰＤＦ
下の図は、１辺が３ｃｍの正方形ＡＢＣＤとＡＢ、ＡＥ、ＢＥの長さがそれぞれ３ｃｍ、４ｃｍ、５ｃｍの直角三角形ＡＢＥを重ねたものです。点Ｐは正方形ＡＢＣＤの辺上を、毎秒１ｃｍの速さでＡ→Ｂ→Ｃ→Ｄの順に移動し、Ｄで止まります。点Ｑは直角三角形ＡＢＥの辺上を、毎秒１ｃｍの速さでＡ→Ｅ→Ｂの順に移動し、Ｂで止まります。ＰとＱが頂点Ａを同時に出発するとき、次の問いに答えなさい。
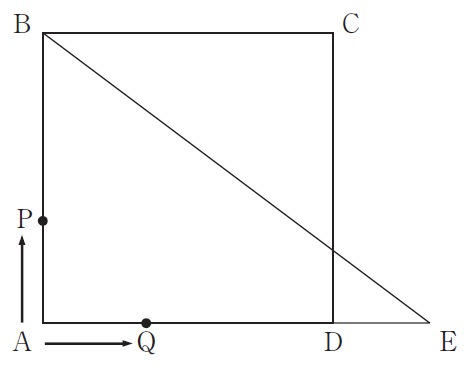
（１） 正解率54.5％
三角形ＡＰＥの面積と三角形ＡＱＣの面積がはじめて等しくなるのは、
出発してから何秒後ですか。
（２） 正解率52.4％
３点Ａ、Ｑ、Ｃが一直線に並ぶのは、出発してから何秒後ですか。
（３） 正解率5.3％
三角形ＡＰＥの面積と三角形ＡＱＣの面積が２回目に等しくなるのは、
出発してから何秒後ですか。
なお、この問題は解答までの考え方を表す式や文章・図などを書きなさい。
＠解説＠
（１）
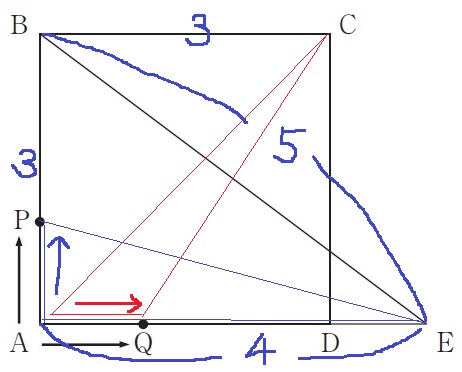
△ＡＰＥは高さが、△ＡＱＣは底辺が伸びる。
３秒後にＰがＢに着くと、△ＡＰＥは６ｃｍ2、△ＡＱＣは4.5ｃｍ2
→０～３秒の間では面積が等しくならない。
３～６秒で△ＡＰＥの面積は６ｃｍ2で変わらず。
４秒後にＱがＥにつくと、三角ＡＱＣは６ｃｍ2になる。
よって、６秒後。
（２）
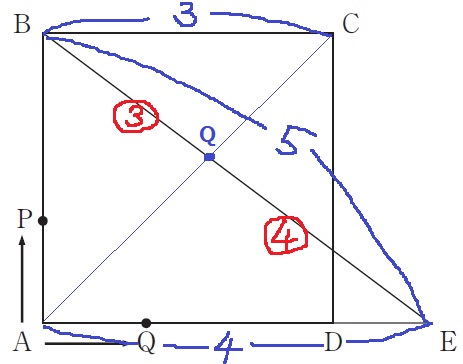
△ＢＣＱ∽△ＥＡＱより、ＢＱ：ＥＱ＝ＢＣ：ＥＡ＝３：４
ＥＱ＝５×４/７＝20/７ｃｍ
Ｑは４＋20/７＝48/７ｃｍ動き、毎秒１ｃｍだから、48/７秒後。
（３）
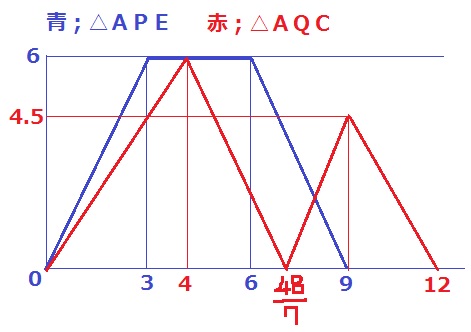
（軸の成分を書き忘れてしまった…縦が面積で横が秒数です）
９秒後のＱはＢにおり、△ＡＱＣは正方形の半分になる。
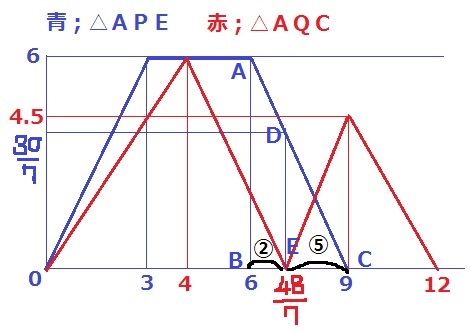
△ＡＢＣ∽△ＤＥＣに注目！
ＢＥ＝48/７－６＝６/７
ＥＣ＝９－48/７＝15/７
ＢＥ：ＥＣ＝６/７：15/７＝２：５
ＡＢ：ＤＥ＝７：５なので、ＤＥ＝６×５/７＝30/７
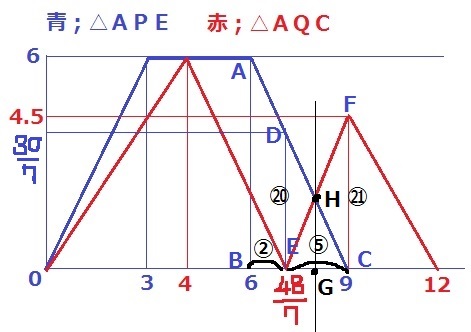
２回目に面積が等しくなる時間をＧ、グラフの交点をＨとする。
△ＤＥＨ∽△ＣＦＨより、
ＥＧ：ＧＣ＝ＤＥ：ＣＦ＝30/７：９/２＝20：21
ＧＣ＝15/７×21/41＝45/41
よって、Ｇの時間は、９－45/41＝324/41秒後
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント