2022年度　海城中学２回目過去問【算数】大問３解説

問題ＰＤＦ
整数ＡをＢ個かけ合わせた数をＡ^Ｂで表すことにします。
例えば、７^２＝７×７＝49、７^４＝７×７×７×７＝2401です。
次の問いに答えなさい。

（１）
７^８の千の位、百の位、十の位、一の位の数をそれぞれ求めなさい。

（２）
７^20の千の位、百の位、十の位、一の位の数をそれぞれ求めなさい。

（３）
７^100の千の位、百の位、十の位、一の位の数をそれぞれ求めなさい。

７⁸＝（７×７×７×７）×（７×７×７×７）＝７⁴×７⁴
（７を８回かけた数＝７を４回かけた数を２回かけた数）
問題文より、７^４＝2401だから、

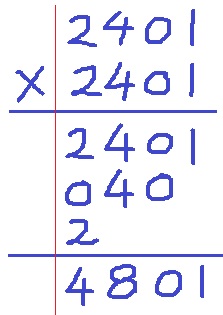
下４桁のみを計算すると4801。
千の位…４、百の位…８、十の位…０、一の位…１

（２）
前問の〔４８０１〕の数字の並びをみると、下２桁が〔０１〕なので計算がしやすい。
７⁸＝７⁴×７⁴ → ８＝４＋４
指数の和が20になれば７²⁰になるはず。
７²⁰＝７⁸×７⁸×７⁴（20＝８＋８＋４）

下４桁だけを計算すると2001。
千の位…２、百の位…０、十の位…０、一の位…１

（３）

７⁸⁰＝8001、７¹⁰⁰は繰り上がりが起きて〔０００１〕。
千の位…０、百の位…０、十の位…０、一の位…１

＠指数法則＠
中学で習う指数法則。
ａ^ｍ×ａ^ｎ＝ａ^ｍ＋ｎ（かけ算は和になる）
ａ^ｍ÷ａ^ｎ＝ａ^ｍ－ｎ（割り算は差になる）
（ａ^ｍ）^ｎ＝ａ^ｍ×ｎ（ａをｍ回かけた数をさらにｎ回かけた数）
e.g.)２⁶⁴÷２⁶⁰＝２^64-60＝２⁴＝16
e.g.)２⁶⁴＝２^2×32＝（２²）³²＝４³²＝４^2×16＝（４²）¹⁶＝16¹⁶
難関中（算数科）解説ページに戻る