2024年度　大阪星光学院中学過去問【算数】大問５解説

問題ＰＤＦ
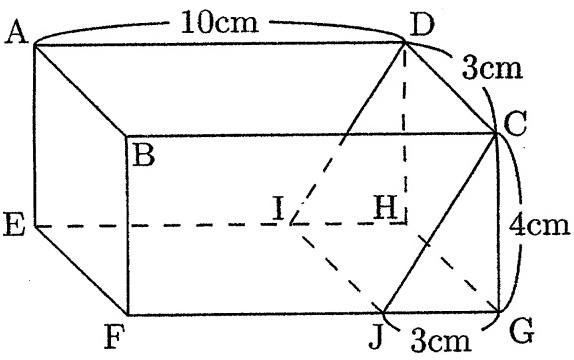
下の図のような面ＡＢＣＤのあいた直方体の容器に、中身のつまった三角柱ＣＪＧ―ＤＩＨをうめこんだ容器が、平らな床に置いてあります。

（１）
水が容器いっぱいに入っている状態で、辺ＧＨを床につけたままこの容器を45度かたむけました。
このとき、容器に残った水は〔　　　〕ｃｍ³です。

（２）
水が容器いっぱいに入っている状態で、辺ＧＨを床につけたままこの容器をかたむけた後、
もとに戻したところ、はじめに入っていた水の５/17だけ容器に残りました。
このとき、水面の高さは〔　　　〕ｃｍです。

（３）
水が容器いっぱいに入っている状態で、辺ＦＧを床につけたままこの容器を45度かたむけました。
このとき、容器に残った水は〔　　　〕ｃｍ³です。

＠解説＠
（１）

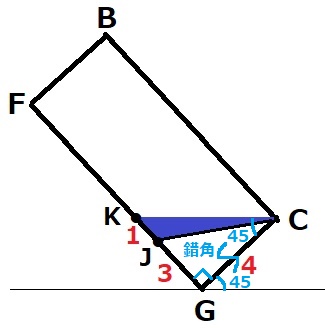
面ＢＦＧＣから見ると、水面はＣを通り、床に平行である。
水面の左端をＫとする。
錯角で45°をあげると、△ＫＧＣの内角は45°―45°―90°だから直角二等辺三角形。
ＫＧ＝ＣＧ＝４ｃｍ
ＫＪ＝４－３＝１ｃｍ
水の体積は、１×４÷２×３＝６ｃｍ³

（２）

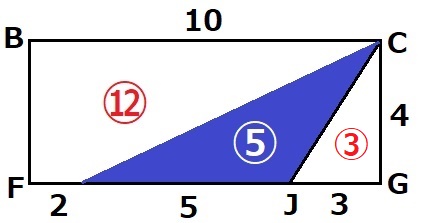
↑傾いているときの様子。
容器：水＝⑰：⑤
台形ＢＦＪＣの上底ＢＣと下底ＦＪの和がちょうど17ｃｍなので、
線分の比がそのまま面積比に相当する。△ＣＪＧ＝③

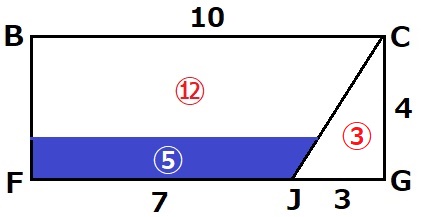
傾きを戻す。このときの水面の高さが答えになる。

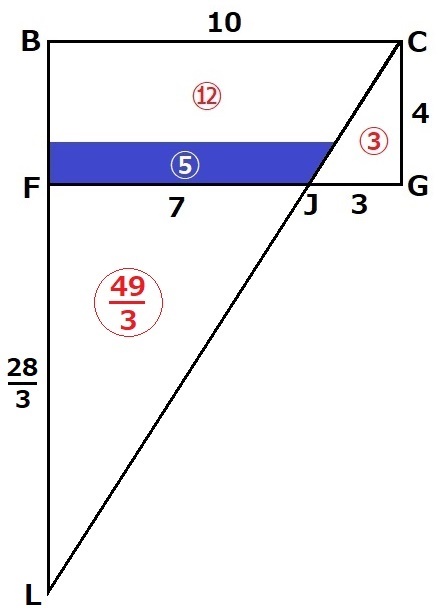
ＢＦとＣＪを延長、交点をＬとする。
△ＣＧＪと△ＬＦＪは相似、ＦＬ＝４×７/３＝28/３ｃｍ
面積比は３×３：７×７＝９：49なので、
△ＬＦＪの面積は、③×49/９＝〇49/３

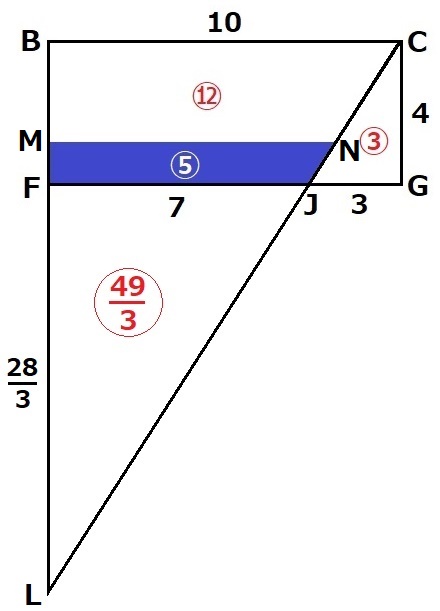
水面をＭＮとする。△ＬＦＪと△ＬＭＮも相似。
△ＬＭＮ＝〇49/３＋⑤＝〇64/３
△ＬＦＪ：△ＬＭＮ＝〇49/３：〇64/３＝49：64
→相似比はＬＦ：ＬＭ＝７：８
水面の高さＭＦは、28/３×１/７＝４/３ｃｍ

（３）

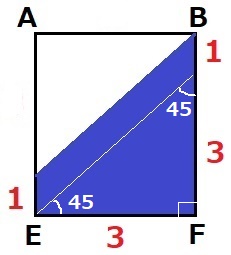
面ＡＥＦＢから水面の様子を調べる。
水面はＢに触れるので、Ｂを通る45度線をひく。
反対側はＥの上１ｃｍ。

求積すべき立体はこのような姿になる。

ＩＪを通る垂直な平面で切断すると、左は四角柱、右は角錐台になる。
左の四角柱は、（１＋４）×３÷２×７＝105/２ｃｍ³

右の角錘台を奥側へ延長する。
高さに注目すると、相似比は小さい三角柱：大きい三角柱＝１：４
→ＩＪ＝３ｃｍより、三角錐の頂点はＩから奥１ｃｍ。
体積比は１×１×１：４×４×４＝１：64
角錐台の体積比は63。
４×３÷２×４÷３×63/64＝63/８ｃｍ³
立体の体積は、105/２＋63/８＝483/８ｃｍ³
難関中（算数科）解説ページに戻る