2019年度　和歌山県公立高校入試問題過去問【数学】解説

問題ＰＤＦ

大問１（小問集合）

（１）①
６－９＝－３

②
４＋２÷（－３/２）
＝４－４/３＝８/３

③
３（２ｘ－ｙ）＋２（４ｘ－２ｙ）
＝６ｘ－３ｙ＋８ｘ－４ｙ
＝14ｘ－７ｙ

④
√32－√18＋√２
＝４√２－３√２＋√２
＝２√２

⑤
（ａ＋２）（ａ－１）－（ａ－２）²
＝ａ²＋ａ－２－ａ²＋４ａ－４
＝５ａ－６

（２）
ｘ²－９ｘ 　←共通因数ｘでくくる
＝ｘ（ｘ－９）＝０
ｘ＝０、９

（３）
縦ｘ、横ｙ、周囲の長さ20ｃｍ。
２（ｘ＋ｙ）＝20
ｘ＋ｙ＝10
ｙ＝－ｘ＋10
一次関数の形なのでウ。

（４）
ａ＝１のとき、ｂ＝１
ａ＝２のとき、ｂ＝１、２
ａ＝３のとき、ｂ＝１、３
ａ＝４のとき、ｂ＝１、２、４
ａ＝５のとき、ｂ＝１、５
ａ＝６のとき、ｂ＝１、２、３、６
14/36＝７/18

（５）

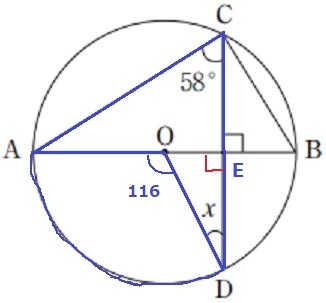
弧ＡＤに対する円周角∠ＡＣＤに注目。
中心角にあたる∠ＡＯＤ＝58×２＝116°
△ＯＤＥで外角定理。
∠ｘ＝116－90＝26°

大問２（小問集合２）

（１）①
ℓ＝２ａ＋πｂ
２ａ＝ℓ－πｂ
ａ＝（ℓ－πｂ）/２＝ℓ/２－πｂ/２

②
説明問題。過程も記述する。
直線部分のａは等しいので、半円部分のｂだけ考える。
左右の半円を合わせると円になる。
直径×πをして、第１レーンと第４レーンの走者がカーブで走る距離の差を算出。
第１レーンは、（ｂ＋0.2×２）×π＝πｂ＋0.4π
第４レーンは、（ｂ＋3.2×２）×π＝πｂ＋6.4π
6.4π－0.4π＝６π
第４レーンの走者は第１レーンの走者より、カーブで６πｍ多く走る。
よって、第４レーンは第１レーンより、スタートラインの位置を６πｍ前に調整するとよい。
*最後は、問題文の言い回しに沿って結論を述べよう。

（２）①
母集団…統計の対象となる集団全体。
標本…サンプル。母集団から抽出された一部。
標本調査は母集団のなかから無作為に標本を取り出し、
標本で得られた結果は母集団も同様とみなして母集団を推定する。
母集団－ア、標本－ウ
*母集団すべてを調べる統計調査は全数調査という（ex.国勢調査）。

②
無作為に取り出した300個のうち、
印あり：印なし＝12：288
600×300/12＝15000個

（３）
花束Ａがｘ束、花束Ｂがｙ束と指定されている。
白色の花は花束Ａで８本、花束Ｂで６本使い、過不足なく使われるようにするので、
８ｘ＋６ｙ＝200　…①
もう１つは、売り上げの合計から立式。
800ｘ＋400ｙ＝16000…②
これを解くと、ｘ＝10、ｙ＝20

花束Ａは10束、花束Ｂは20束。
赤色の花はＡで10本、Ｂで２本使われ、80本余ったので、
10×10＋２×20＋80＝220本

大問３（規則）

（１）①
第１列と第２列を一体化し、テーブル７卓を１つのグループにまとめる。
（第１列、第２列）（第３列、第４列）（第５列、第６列）…（第19列、第20列）
20÷２＝10グループある。
１グループはテーブル７卓なので、
第20列の最後のテーブル番号は、７×10＝70番
１つのテーブルに座席は６つあるから、
６×70＝420席

②
前問のグループ（テーブル７卓を１つとした集団）を再度利用する。
１グループ目の最初のテーブル番号は１番。
２グループ目の最初（第３列左）は８番。
３グループ目の最初（第５列左）は15番。
４グループ目の最初（第７列左）は22番。
第７列の最も左側にあるテーブル番号は22番。

（２）
１卓のテーブルに６つの座席番号が割り振られるので、
176÷６＝29・・２
つまり、176番の和歌子はテーブル番号が30番で、
アから数えて２つ目の席にいる。
30番、イ

（３）

テーブル番号を６倍すると、最も大きい座席番号。
最も大きい座席番号－２＝正面から最も遠い座席番号。
６ａ－２＝ｂ
ｂ＝６ａ－２

（４）
連続する６つの整数が３の倍数であることの証明とほぼ同じ。
最も小さい番号をｎとおくと残りの座席は、
ｎ＋１、ｎ＋２、ｎ＋３、ｎ＋４、ｎ＋５と表せる。
ｎ＋（ｎ＋１）＋（ｎ＋２）＋（ｎ＋３）＋（ｎ＋４）＋（ｎ＋５）
＝６ｎ＋15＝３（２ｎ＋５）
２ｎ＋５が自然数だから、３（２ｎ＋５）は３の倍数。
したがって、すべてのテーブルの６席の座席番号の和は３の倍数になる。

大問４（関数）

（１）
ｙ＝１/２ｘ²において、
ｘ＝０のとき、ｙ＝０
ｘ＝２のとき、ｙ＝２
（２－０）/（２－０）＝１

（２）
平行四辺形は対辺の長さが等しい。
ＡＢ＝ＱＰ

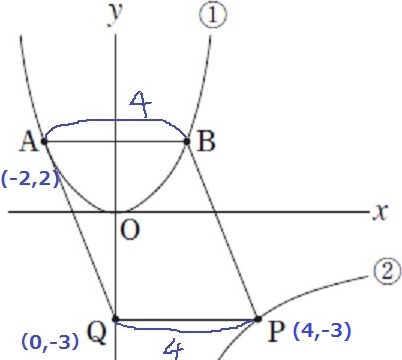
Ｐのｘ座標が４となり、ｙ＝－12/ｘに代入。
Ｐ（４、－３）
Ｑ（０、－３）
Ａ⇒Ｑ、右に２、下に５だから傾きは－５/２
ｙ＝－５/２ｘ－３

（３）
ｙ＝１/２ｘ²から、Ｒ（１、１/２）

△ＣＱＢ∽△ＤＱＲ
ＣＱ：ＤＱ＝ＣＢ：ＤＲ＝２：１
Ｑのｙ座標は、１－３/２＝－１

Ｐはｙ＝－12/ｘ上の点なので、
－１＝－12/ｘ
ｘ＝12
Ｐ（12、－１）

（４）
Ｂのｘ座標２から、Ｐ（２、－６）

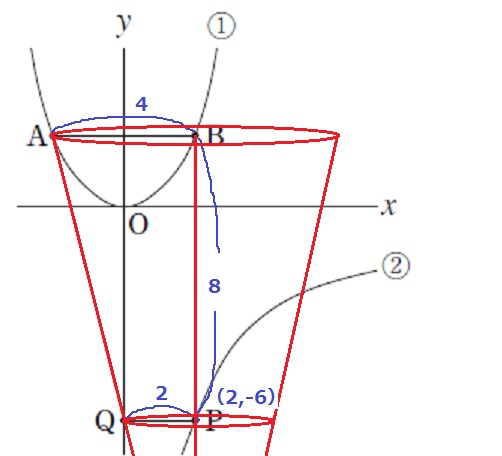
あとは、お馴染みのやり方。
延長すると高さ16の円柱で、その体積の７/８倍。
４×４×π×16×１/３×７/８＝224π/３ｃｍ³

大問５（平面図形）

（１）①

ＢＥ＝③、ＥＣ＝②、ＡＤ＝⑤
△ＦＢＥ∽△ＦＤＡ
ＡＦ：ＦＥ＝ＡＤ：ＥＢ＝５：３

②
前問とは別の問題であることに注意。

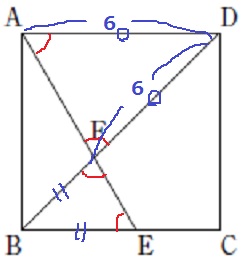
対頂角と錯角で、４つの角が等しい。
△ＡＤＦは二等辺三角形。
ＤＦ＝ＤＡ＝６ｃｍ
ＢＤは正方形の対角線で６√２ｃｍ
ＢＦ＝６√２－６ｃｍ

（２）①

正方形の１辺で、ＡＢ＝ＨD
∠ＡＢＥ＝∠ＨＤＧ＝90°

正方形の対角線は45°。
ＢＤ//ＥＧで45°を同位角で移動させると、
△ＥＣＧが直角二等辺三角形とわかる。
ＢＥ＝ＢＣ－ＥＣ
ＤＧ＝ＤＣ－ＧＣ
ＢＣ＝ＤＣ、ＥＣ＝ＧＣより、
ＢＥ＝ＤＧ
２辺とあいだの角が等しいので合同。

＠余談＠
ＢＥ＝ＤＧは平行線と線分の比でもＯＫ。
ＢＥ：ＥＣ＝ＤＧ：ＧＣ
ＢＣ（ＢＥ＋ＥＣ）＝ＤＣ（ＤＧ＋ＧＣ）より、ＢＥ＝ＤＧ

Ｃを回転の中心として、時計回りに90°回転移動させると…。

②
角度の調査から。

△ＡＢＥは30°－60°－90°の直角三角形。
∠ＩＡＤ＝90－30＝60°
先ほどの合同から、∠ＤＨＧ＝∠ＢＡＥ＝30°
△ＡＩＨも30°－60°－90°の直角三角形。

ＡＨ＝12ｃｍ
△ＡＩＨの辺の比１：２：√３からＡＩ＝６ｃｍ、ＩＨ＝６√３ｃｍ

Ｃが求めたいところ。
Ｃ＝正方形－（Ａ＋Ｂ）＝正方形－△ＡＩＨ（＝Ａ＋Ｂ）
四角形ＩＥＣＧ＝６×６－６√３×６÷２
＝36－18√３ｃｍ²
公立高校入試解説ページに戻る