2018年度　栄東中学過去問・東大特待【算数】大問４解説

問題ＰＤＦ
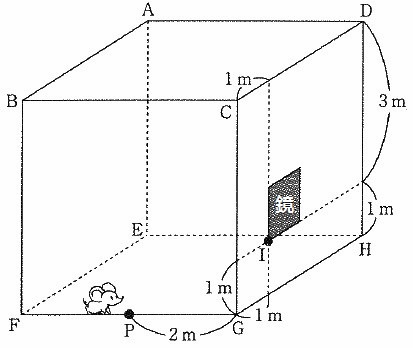
図のように、１辺の長さが４ｃｍの立方体の形をした部屋のかべに１辺の長さが１ｍの正方形の鏡があります。また、床のP地点の鏡のあるかべからは２ｍ離れています。このとき、P地点から鏡を通して見ることのできる部分について考えます。

（１）
Ｐ地点から見て、鏡の右下のＩの部分にうつってるのは、
ＡＢＦＥのかべのどの部分か、解答欄の図に●を書き込みなさい。

（２）
ＡＢＦＥのかべのうち、Ｐ地点から見て、鏡を通してみることのできる部分の面積を求めなさい。

（３）
この部屋のかべと天井のうち、Ｐ地点から見て、鏡を通して見ることのできる部分を解答欄の図に書き込み、
その面積を求めなさい。


↑《この図を使って考えてよい》

（１）

コツはＰを通り、面ＣＧＨＤに平行な面を作図。
面ＣＧＨＤ方向からみると、奥行きＰＧ＝２で右に１、上に１となり、
ＰからＩで反射して平行面にあたると、ちょうど立方体の中央にくる。
そこから、同様に奥行きＦＰ＝２で面ＣＧＨＤからみると右１上１のＩ’となる

（２）（３）

鏡の残りの頂点をＪ・Ｋ・Ｌとして、３方向から四苦八苦しつつ作図するとこうなる↑
天井には点線がないので、あらかじめ中点を通る２本の補助線をひいておいた方がいい。
面ＣＧＨＤ方向からみて、奥行きＰＧ＝２を進む間にどれほど右上にいくかを見極める。
Ｌは背面ではなく、天井にぶつかる。

鏡の反射でみえる範囲は、四角形ＡＮＩ’Ｍ、ＡＭＪ’Ｋ’、ＡＮＬ’Ｋ’のところ。
（２）１×１＝１ｍ²
（３）１＋（１＋２）×２÷２×２＝７ｍ²
難関中（算数科）解説ページに戻る