平均47.3点(前年比;+5.0点)

問題はこちら→リセマムさん
出題範囲の除外はないが、『主として基礎的・基本的な事項及び思考力・判断力・表現力などを
検査できるものを出題するものとする』
大問1(小問集合)-69.0%
(1)① 96.0%
5×4+7
=27
② 89.6%
2/3-3/5÷9/2
=2/3-2/15
=8/15
③ 85.6%
√6×√8-9/√3
=4√3-3√3
=√3
④ 54.9%
20分は1/3時間。
4km÷1/3時間=時速12km
⑤ 30.5%!

正四面体は4つの正三角形からなる。
辺の数は6本。
(2) 82.1%
7x-3a=4x+2a
5a=3x=3×5=15
a=3
(3) 59.8%
底面は3:4:5の直角三角形→高さは4cm
3×4÷2×7=42cm3
(4) 62.8%
28=22×7
『ある自然数の2乗』→平方数は各素因数が偶数個。
7をかければ22×72=142で平方数。
n=7
(5) 59.4%

『約47%多い』ということは、1193を【147】としたときの【100】が答え。
概算で処理しよう。
1193→1200、【147】→【150】とみなすと、
1200×【100】/【150】=800
これに近いのは平成29年。ウ
大問2(小問集合2)-55.9%
(1) 74.7%

半円の弧に対する円周角は直角→∠ADC=90°
∠DCA=180-(26+90)=64°
弧ADに対する円周角より、∠x=64°
(2) 50.6%
和が11以上は(5、6)(6、5)(6、6)の3通りしかない。
和が10以下は、6×6-3=33通り
確率は、33/36=11/12
(3) 65.8%
(x+3)2-2(x+3)-24 ←(x+3)をXをおく
=X2-2X-24
=(X-6)(X+4) ←Xを(x+3)に戻す
=(x+3-6)(x+3+4)
=(x-3)(x+7)
(4) 23.3%!
△AGL∽△BIHの証明。
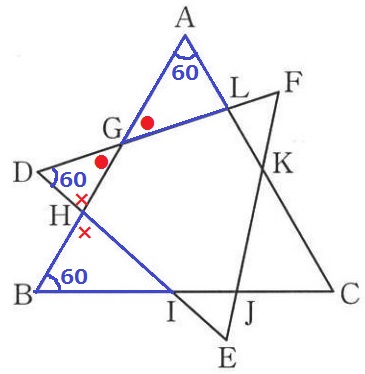
△DGHを媒介にすればいい。
正三角形の内角60°と対頂角で2角相等。
△AGL∽△DGHを指摘し、同様の手段で△DGH∽△BIHとなり、
△AGL∽△DGH∽△BIH→△AGL∽△BIHが導ける。
(5) 71.0%
答案では方程式と計算過程も記述する。
Mサイズをx枚、Lサイズをy枚とする。
ペットボトルの個数で等式。
5x+8y=70 …①
代金で等式。
3x+5y=43 …②
①と②の連立を解く。
サボは②×5-①×3をしました。
x=6、y=5
Mサイズ…6枚、Lサイズ…5枚
大問3(データの活用)-51.3%
(1) 87.4%
問題文より、20冊以上30冊未満は6人
表から、b=40-(3+5+6+10+7)=40-31=9人
a…6、b…9
(2) 13.9%!
40人の中央値(メジアン)は20番目と21番目の平均。
20冊未満の合計が8人。残りは問題文の情報を手がかりに数える。
20番目が35冊、21番目が36冊、その間は35.5冊。
(3)① 64.0%
40冊以上50冊未満は7人。
相対度数は、7÷20=7/20=35/100=0.35
② 39.7%

図にあるAの度数を表の横に書き足す。Bの度数も出しておく。
ア:0~30冊はA…5人、B…9人。Bの方が多い。〇
イ:20人の中央値は10番目と11番目の平均。A…35冊、B…35冊で同じ。×
ウ:最頻値(モード)は最もあらわれている値。A…45冊、B…55冊でBが多い。〇
エ:最も差が大きい階級は40冊以上50冊未満。×
ア・ウ
大問4(関数)-33.1%
(1) 82.3%
y=2x2にx=3を代入。
y=2×32=18
(2)イ…57.6%、ウ…17.9%!
Cのx座標は、-1+2=1
y=2×12=2
C(1、2)
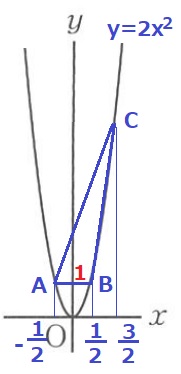
ABはx軸に平行で距離が1
Bのx座標は1/2
Cのx座標は、1/2+1=3/2
Cのy座標は、y=2×(3/2)2=9/2
C(3/2、9/2)
イ…(1、2)ウ…(3/2、9/2)
(3)① 25.8%!
Aのx座標がt
Bのx座標はt+1、Cはt+2
2x2のxをt+2に置き換えればいい。
Cのy座標は、2(t+2)2
② 2.4%!!
説明問題。大変です(;´・ω・)
問題文の流れから、△ABCの面積は2で一定のような気がする。
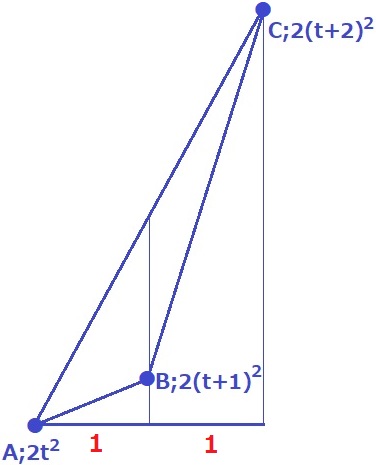
↑Aのx座標が正なので、AB、BCは右上の線分。
x座標の差は1。各点はy座標だけ示しています。
△ABCの面積を出して変数tが残れば、tの値によって面積が変わる。
変数tがなければ△ABCの面積は一定である。
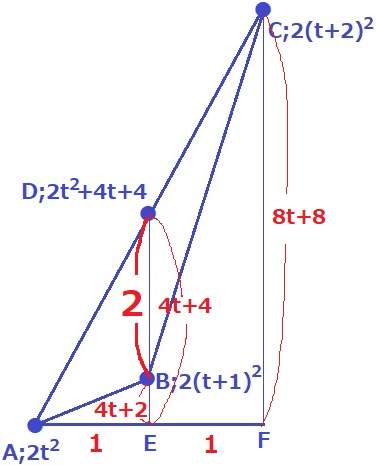
ACの中点をD、DとCの下にそれぞれE、Fをおく。
CF=2(t+2)2-2t2=8t+8
中点連結定理から、DE=CF÷2=(8t+8)÷2=4t+4
BE=2(t+1)2-2t2=4t+2
DB=(4t+4)-(4t+2)=2
△ABCは幅AF=2、高さDB=2だから、面積は2×2÷2=2
△ABCの面積は点Aのx座標がどのような値でも2である。
大問5(総合問題)-34.3%
(1) 50.5%
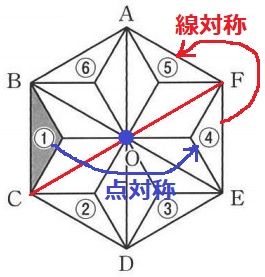
点Oを回転の中心として点対称➡④
CFを対称の軸として線対称➡⑤
@薩摩切子@
江戸切子は耳にしたことありますが、薩摩にもあったとは(;`ω´)

なんでも鑑定団で2000万円の鑑定額がでました。もともとガラス工芸は出島のあった長崎から徐々に広がり、江戸切子のあとを追うように薩摩藩でも産業として振興しました。うえのサイトによると、特に紅色は着色剤の調合や温度管理が難しく、国内ではじめて成功したのが薩摩藩であったそうです。幕末~明治初期の混乱で一時は途絶えた薩摩切子を、およそ100年後に島津家が復活させたんだとか。
(2) 54.3%
1本の対角線から正六角形を作図する。

↑円に内接する正六角形を思い浮かべよう。
正六角形を6分割すると6つの正三角形があらわれる。
→円周を6分割すると正六角形の頂点ができる。

①ADの垂直二等分線。対角線ADの中点が円の中心である。
②円の作図。
③△ABOは正三角形。AOの長さをとり、Aから出発して円周を6等分。
これらを結んで正六角形ができる。
(3)① 43.6%
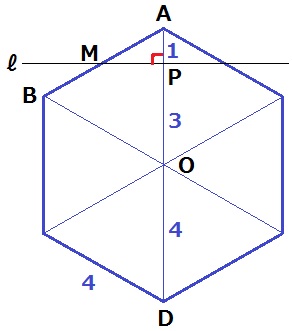
これも正六角形の分割から考えるとPの位置が特定しやすい。
ADの中点をOとする。正三角形ABOからAO=4cm
ℓがBにきたとき、PはAOの中点にあり、AP=2cm
Pが出発して1秒後ということは、MはAB上にいる。
△AMPの内角は30°-60°-90°の直角三角形で辺の比は1:2:√3
PM=√3cm
② 21.9%!
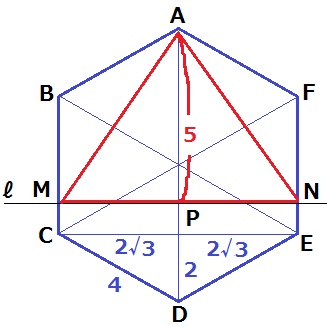
5秒後のℓはCより上。AP=5cm
底辺MNはCEに等しい。
1辺4cmの正三角形の高さである2√3を2倍して、MN=4√3cm
△AMNの面積は、4√3×5÷2=10√3cm2
③ 4.4%!!
ラストに説明問題。
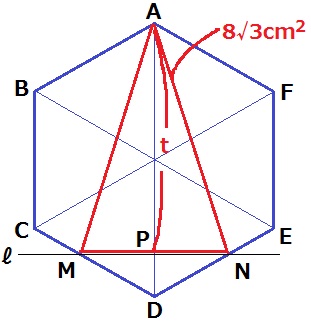
MがCD上にあるので、6≦t≦8
(あとの計算で使うので、tの範囲は定めておく)
△AMNの高さはt。底辺MNの長さがわかればいい。
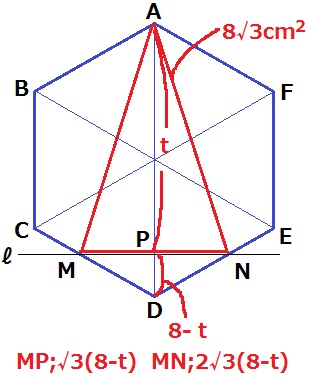
PD=8-tcm
△MPDは1:2:√3の直角三角形ゆえ、MP=√3(8-t)cm
MN=2√3(8-t)cm
2√3(8-t)×t÷2=8√3
t(8-t)=8
t2-8t+8=0
解の公式を適用。tの係数が偶数だからb=2b’が使える。
t=4±2√2
6≦t≦8より、t=4+√2
4+2√2秒後
●講評●
大問1
(5)47%多い→もとを100%としたら147%。
大問2
(4)3つの三角形が∽。△EIJ、△CKJ、△FKLも∽。
大問3
(2)折れ線の情報を度数分布表に足す。
関連する情報は近くに書いた方が良い。
大問4
(3)②この説明はツライ…。後回し推奨。
大問5
(1)点対称&線対称。
(2)正六角形の作図。6分割スタイルを思い浮かべる。
円の半径は正三角形の1辺に相当する。
(3)Mがどの辺上にあるかを見極める。
③底辺MNの長さは下にある△DMNから導く。



コメント