問題ＰＤＦ
太郎くんと次郎くんはそれぞれ通っている学校の周りを見渡しました。
（１）
太郎くんの通っている学校からは、白か黒のどちらかの一色で塗られたビルとタワーがたくさんあります。
いま、ビルとタワーについて次の３つの情報がわかっています。
・高さが50ｍ以下であるものはすべてビルです。
・白いタワーは１つもありません。
・ビルとタワーは少なくとも１つずつあります。
このとき、次の問いに答えなさい。
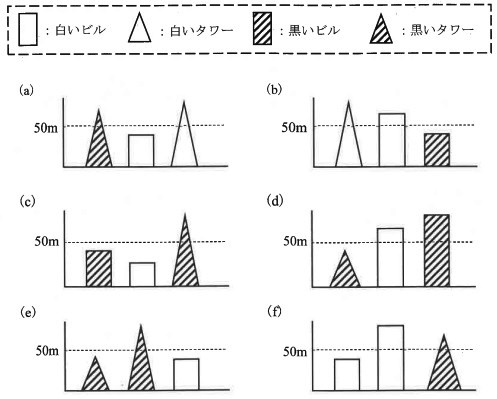
①下の（ａ）～（ｆ）のうち、３つの情報全部にあてはまるものをすべて選びなさい。
②次のア～カのうち、３つの情報から確実に言えることをすべて選びなさい。
ただし、ビルとタワーを合わせて建物と呼ぶことにします。
◆情報再掲◆
・高さが50ｍ以下であるものはすべてビルです。
・白いタワーは１つもありません。
・ビルとタワーは少なくとも１つずつあります。
ア：タワーは50ｍより高い。
イ：50ｍより高いビルはない。
ウ：白いビルはタワーより高くない。
エ：タワーは必ず黒い。
オ：50ｍより高くて白い建物はない。
カ：50ｍより高くて白い建物がある。
（２）
次郎くんの通っている中学校からはスカイツリーや富士山が見えました。
下の写真はその中学校から撮ったものです。
いま、次の４つの情報がわかっています。
・写真を撮った地点の高さは22ｍです。
・スカイツリーの高さは634ｍです。
・この写真では、富士山の高さはスカイツリーの８分の５の高さに見えます。
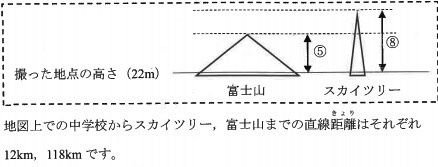
４つの情報から富士山の高さを計算しなさい。
ただし、答えの単位はｍで答えること。
＠解説＠
（１）①
条件に沿わないものを消していく。
・高さが50ｍ以下であるものはすべてビルです。
⇒50ｍより高いビルがある、ｂ、ｄ、ｅを除外。
・白いタワーは１つもありません。
⇒白いタワーがあるａ除外。
・ビルとタワーは少なくとも１つずつあります。
⇒いずれもビルとタワーがある。
残ったｃ・ｆが答え。
②
論理形式。
必ず成立することを真という。必ず成立しないことを偽という。
『Ｐであれば、Ｑが成立する』（Ｐ→Ｑ）
Ｐは仮定、Ｑは結論といい、Ｐ→Ｑを真とする。
『Ｑならば、Ｐが成立する』（Ｑ→Ｐ）
これを逆といい、逆は偽となる（必ずしも成立しない）。
『Ｐでないのならば、Ｑは成立しない』（Ｐ×→Ｑ×）
これを裏といい、裏は偽となる（必ずしも成立しない）。
『Ｑでないのならば、Ｐは成立しない』（Ｑ×→Ｐ×）
これを対偶といい、対偶は真となる（必ず成立する）。
◆条件再掲◆
①高さが50ｍ以下であるものはすべてビルです。
②白いタワーは１つもありません。
③ビルとタワーは少なくとも１つずつあります。
建物の要素はビルかタワーのどちらか。
（ビルでなければタワー、タワーでなければビルの関係）
色の要素は黒か白（黒でなければ白、白でなければ黒）
①『50ｍ以下→ビル』
①’対偶は『タワー→50ｍより高い』（タワーであれば、必ず50ｍより高い）
②白いタワーはない⇒タワー→黒（タワーであれば、必ず黒）
②’対偶は『白→ビル』（白い建物であれば、必ずビル）
③ビルとタワーの２つの建物がある。
◆検討◆
*仮定『～であれば』（矢印の左側の内容）が条件にないものは確実に言えない。
ア：タワーは50ｍより高い。⇒①’対偶から真。
イ：50ｍより高いビルは無い。
⇒『50ｍより高い建物であれば～』がどこにもないので、確実に成り立つとはいえない。
ウ：白いビルはタワーより高くない。
⇒②’対偶より『白い建物はビル』といえるが、『(白い)ビルであれば～』が無い。
エ：タワーは必ず黒い。⇒②より真。
オ：50ｍより高くて白い建物はない。
カ：50ｍより高くて白い建物がある。
⇒『50ｍより高い、かつ白い』建物の情報がない。
*②’対偶の『白い』と、『50ｍより高い、かつ白い』は異なる仮定。
①’と②をあわせると、「タワーであれば、50ｍより高く、かつ黒い」になる。
（③より、50ｍより高くて黒い建物（タワー）はあることになる）
ア・エ
類題をＱＵＩＺで出題したので、挑戦したい方はぜひどうぞ。
下は〔かつ・または〕を伴うド・モルガンの法則を利用する問題です。
レべルは高校生以上です。
（２）
写真でみえる高さは、撮影地点の高さ22ｍからみたときの高さ。
対して、『スカイツリーの高さ634ｍ』という情報は、地表からの高さとなる。
写真で見えたスカイツリーの高さは、634－22＝612ｍ
これを⑧としたときに、富士山の高さは⑤に見えた。
写真（12ｋｍ地点）で見えた富士山の高さは、〔612×５/８ｋｍ〕となる。
この長さを×118/12倍すれば、撮影地点の高さから見える富士山の高さが算出され、
＋22ｍで実物の富士山の高さとなる。
612×５/８×118/12＋22＝3761.25＋22＝3783.25ｍ
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント