問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）①
２－６
＝－４
②
８/５＋７/15×（－３）
＝８/５－７/５
＝１/５
③
３（２ａ＋ｂ）－（ａ＋５ｂ）
＝６ａ＋３ｂ－ａ－５ｂ
＝５ａ－２ｂ
④
９/√３－√75
＝３√３－５√３
＝－２√３
⑤
ａ（ａ＋２）＋（ａ＋１）（ａ－３）
＝ａ2＋２ａ＋ａ2－２ａ－３
＝２ａ2－３
（２）
ｘ2－12ｘ＋36
＝（ｘ－６）2
（３）
絶対値…数直線上で原点０からの距離。
０、±１、±２、±３、±４の９個。
（４）ア
16/200＝８/100＝0.08
イ
累積度数…その階級までの度数の合計。
24＋56＋64＝144
（５）
ｙ＝ａｘ2に（ｘ、ｙ）＝（３、－18）を代入する。
－18＝９ａ
ａ＝－２
ｙ＝－２ｘ2
（６）
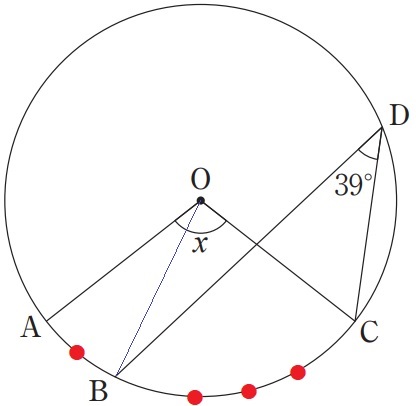
中心角は円周角の２倍、∠ＢＯＣ＝∠ＢＤＣ×２
中心角は弧の長さに比例する。∠ＡＯＣ（ｘ）＝∠ＢＯＣ×４/３
ｘ＝39×２×４/３＝104°
大問２（小問集合２）
（１）①
Ａと重なるのはＥ。
②
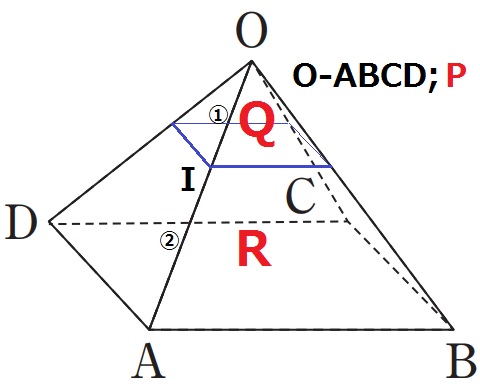
体積比は相似比の３乗。
Ｐ：Ｑ＝①3：③3＝１：27
Ｑ：Ｒ＝１：26
（２）①
【緑・赤・青】を１周期として並べるので、
13÷３＝４…１
余り１は緑。
②
最後のｎ枚目が７ｃｍ。
ｎ－１枚目までが２ｃｍ。
２（ｎ－１）＋７
＝２ｎ＋５
（３）
12の約数は【１・２・３・４・６・12】
積がこれらになる組み合わせを調べる。
１×１、１×２、１×３、１×４、２×２、１×６、２×３、２×６、３×４
１×１と２×２以外は逆もあるので16通り。
全体は６×６＝36通りだから、確率は16/36＝４/９
（４）
答案では求める過程も記述する。
ドーナツをｘ個とすると、カップケーキは18－ｘ個。
25ｘ＋15（18－ｘ）＝400 ←÷５
５ｘ＋３（18－ｘ）＝80
２ｘ＝26
ｘ＝13
カップケーキは18－13＝５個
ドーナツ…13個、カップケーキ…５個
（*公式解答のように連立でもＯＫ）
（５）
平均値より大きい太郎が８番以内に入らない理由を記述する。
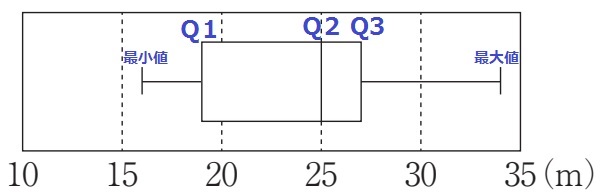
15人のＱ2（中央値；第２四分位数）は、（15＋１）÷２＝８番目の生徒の記録。
『箱ひげ図より、中央値にあたる８番目の生徒の記録が25ｍだから、
それより小さい記録である太郎は８番以内に入らない』
大問３（関数）
（１）
変化の割合＝（ｙの増加量）/（ｘの増加量）
１次関数の変化の割合は傾きと同じで一定。
（ｙの増加量）÷４＝１/２
（ｙの増加量）＝１/２×４＝２
（２）
Ａ（２、４）→Ｐ（６、０）
右に４、下に４だから、傾きは－１。
切片はＡから左に２、上に２移動して６。
ｙ＝－ｘ＋６
（３）
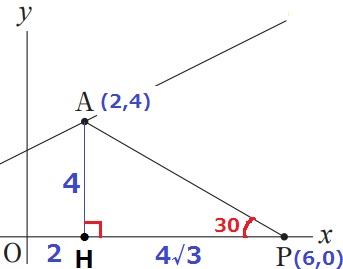
Ａからｘ軸に垂線をおろし、足をＨとする。
Ａ座標より、ＯＨ＝２、ＡＨ＝４
△ＡＨＰは内角が30°―60°―90°、辺の比は１：２：√３だからＨＰ＝４√３
Ｐのｘ座標は、ＯＨ＋ＨＰ＝２＋４√３
（４）
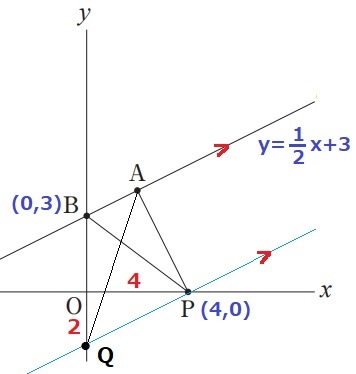
Ｐを通るＡＢに平行な線をひくと、ｙ軸との交点がＱである。
なぜなら、等積変形より△ＡＢＰ＝△ＡＢＱだから。
平行からＰＱの傾きは１/２。
ＯＰ＝４なので、ＯＱ＝２
Ｑ（０、－２）
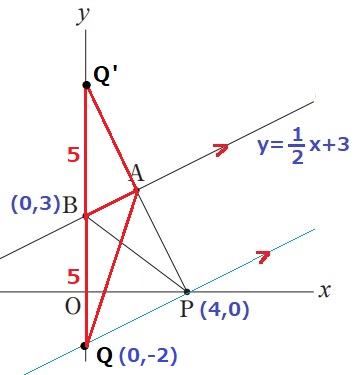
ＢＱ＝３－（－２）＝５
ｙ軸上でＢより上にＱ’Ｂ＝５となるようなＱ’（０、８）をおく。
ＢＱ＝ＢＱ’で底辺共通→△ＡＢＱ＝△ＡＢＱ’だから、△ＡＢＱ’も△ＡＢＰと等積である。
（０、－２）（０、８）
大問４（平面図形）
（１）
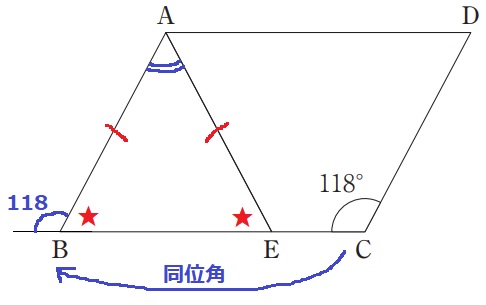
ＡＢ//ＤＣの同位角で118°を移す。
∠ＡＢＥ＝180－118＝62°
△ＡＢＥは二等辺三角形だから、∠ＢＡＥ＝180－62×２＝56°
＠別解＠
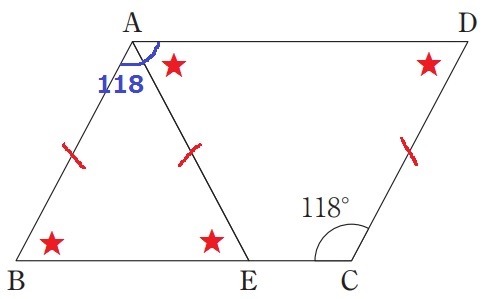
平行四辺形の対辺と対角は等しい。
四角形ＡＥＣＤは等脚台形で★＝62°だから、
∠ＢＡＥ＝118－62＝56°
（２）
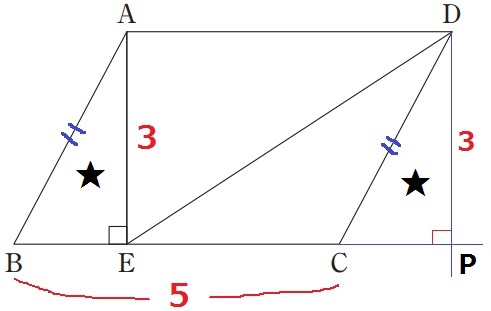
ＤＥを斜辺とする直角三角形を作成する。
Ｄから垂線を下ろし、ＢＣの延長線との交点をＰとする。
平行四辺形ＡＢＣＤの対辺は等しい。ＡＢ＝ＤＣ
平行四辺形の高さより、ＡＥ＝ＤＰ
斜辺と他の１辺が等しい直角三角形から△ＡＢＥ≡△ＤＣＰ
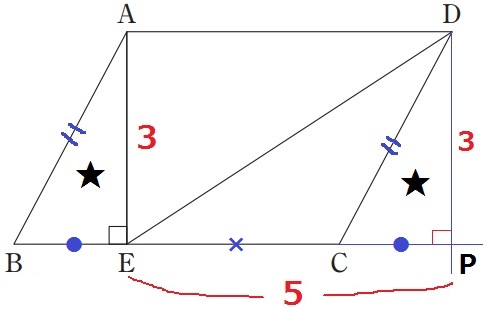
対応する辺で、ＢＥ＝ＣＰ（●）
ＢＥ（●）＋ＥＣ（×）＝ＣＰ（●）＋ＥＣ（×）＝ＥＰ＝５ｃｍ
△ＤＥＰで三平方→ＤＥ＝√34ｃｍ
（３）
四角形ＢＥＤＦが平行四辺形である証明。
『対角線の交点をＯとする』が新情報なので、これをうまく使う。
平行四辺形の対角線はおのおのの中点で交わる。ＯＢ＝ＯＤ
これらを１辺とする△ＯＢＥと△ＯＤＦに着目すると、
ＢＥ//ＦＤの錯角から、∠ＯＢＥ＝∠ＯＤＦ
対頂角で、∠ＢＯＥ＝∠ＤＯＦ
１辺と両端角が等しいので、△ＯＢＥ≡△ＯＤＦ
対応する辺は等しく、ＯＥ＝ＯＤ
四角形ＢＥＤＦの対角線がおのおのの中点で交わるので、
四角形ＢＥＤＦは平行四辺形である。
（４）
ＡＨ//ＢＥ→△ＧＡＨ∽△ＧＢＥより、ＡＨ＝３×２/６＝１ｃｍ
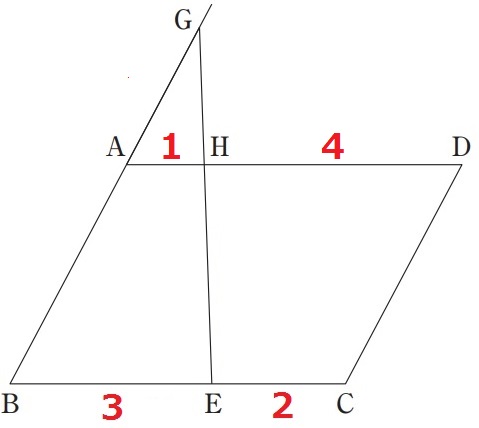
上底＋下底の和から面積比を算出する。
台形ＡＢＥＨ：平行四辺形ＡＢＣＤ
＝ＡＨ＋ＢＥ：ＡＤ＋ＢＣ
＝２：５
台形ＡＢＥＨの面積は平行四辺形ＡＢＣＤの２/５倍。
全体的に計算処理が手軽で、独立した小問が連なる。
大問１
オール基本問題。
（３）０を忘れないように！
（４）累積相対度数もよく出る。
（６）ＯＢに補助線をひいて、∠ＢＯＣの中心角を求める。
大問２
ここも基本なので取りこぼしたくない。
大問３
（３）30°から有名三角形を想起する。
（４）△ＡＢＰと△ＡＢＱはＡＢが共通辺。
ＡＢに平行な線をひき、Ｐをｙ軸上に移す。
もう１つのＱはＢより上側にある。計算もしやすい。
大問４
（２）△ＡＢＥを右側に移動させる。
（３）平行四辺形になる条件は５つある。
『対角線の交点Ｏ』から対角線の条件を使うと察する。
平行四辺形ＡＢＣＤの対角線から、ＯＢ＝ＯＤがいえる。
あとはＯＥ＝ＯＤを指摘するために、△ＯＢＥ≡△ＯＤＦを示せばいい。
（４）ラス問だが難しくはなかった。
上底＋下底の和の面積比は公立高校入試でよく使える技。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
