2024年度　大分県公立高校入試問題過去問【数学】解説

平均30.8点（前年比；＋1.2点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　97.3％
３－７
＝－４

②　87.4％
－４²÷８
＝－16÷８
＝－２

③　80.5％
４ｘ－７－（４＋ｘ）
＝４ｘ－７－４－ｘ
＝３ｘ－11

④　75.9％
３/８ｘ²ｙ³÷３/２ｘｙ
＝ｘｙ²/４

⑤　74.8％
２√３＋√２×６/√６　←後半は√２で約分
＝２√３＋６/√３
＝２√３＋２√３
＝４√３

（２）　72.3％
３ｘ²－５ｘ＋１＝０
解の公式を適用して、ｘ＝（５±√13）/６

（３）　51.9％
ｙ＝－２ｘ²は上に凸のグラフ。
原点を通過するから、ｘ＝０のとき、最大値ｙ＝０
ｘ＝３のとき、最小値ｙ＝－18
－18≦ｙ≦０

（４）　75.2％

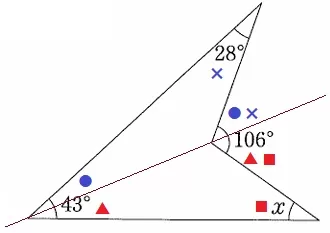
ブーメランの股は３つの角の和。
ｘ＝106－（43＋28）＝35°

（５）　26.1％！

ＡＢが立方体の高さになるように組み立てる。
接する辺を調べてＡＢをイの上部に移すと、
底面と天井はア・ウなので、高さＡＢに垂直な面はア・ウ。

（６）２点…23.4％！、１点…25.9％

弧ＡＣ：弧ＣＢ＝∠ＡＯＣ：∠ＣＯＢ＝⑤：①
∠ＣＯＢ＝180×①/⑥＝30°をつくればいい。

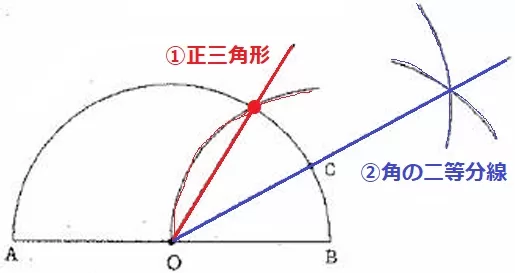
半径ＯＢの長さをとってＢから弧を描き、正三角形をつくる。
60°を二等分して、半円の弧との交点がＣとなる。

大問２（関数）

（１）　65.6%
ｙ＝８/ｘにｘ＝４を代入→Ａ（４、２）
これをｙ＝ａｘ²に代入する。
２＝16ａ
ａ＝１/８

（２）　55.0％
ｙ＝８/ｘにｙ＝４を代入して、Ｂのｘ座標は２。
Ｂ（２、４）→Ａ（４、２）
右に２、下に２だから、傾きは－２/２＝－１
切片はＢから左に２、上に２移動して、４＋２＝６
ｙ＝－ｘ＋６

（３）①　14.6％！

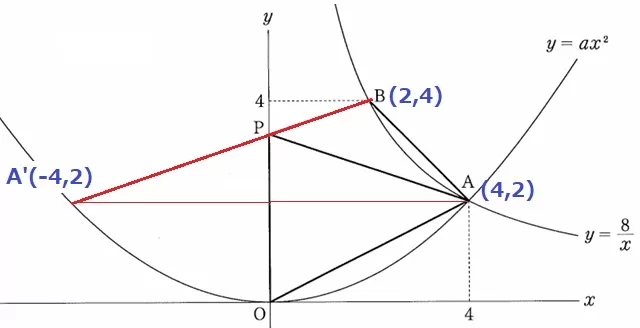
ｙ軸についてＡを線対称移動させたＡ’をつくる。
Ａ’（－４、２）→Ｂ（２、４）
右に６、上に２だから、傾きは２/６＝１/３
Ａ→Ｐは、右に４、上に４×１/３＝４/３なので、
Ｐのｙ座標は、２＋４/３＝10/３

②　9.4％!!
△ＡＢＰの面積比をどう求めるか。

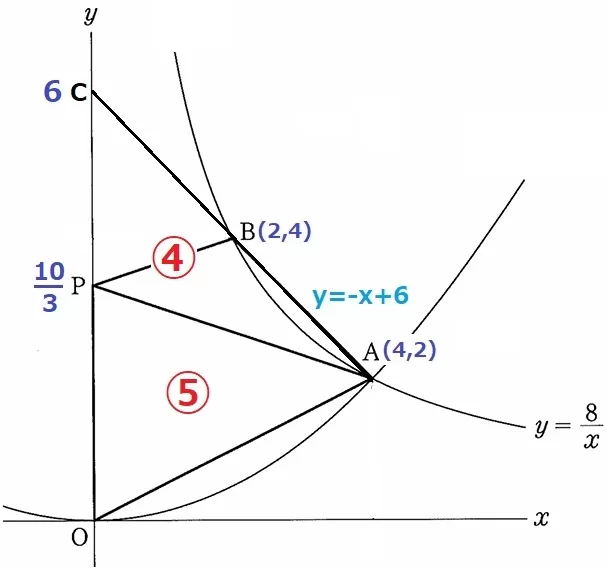
△ＡＰＯがｙ軸に接しているので、ｙ軸上で考える。
（２）ＡＢ；ｙ＝－ｘ＋６の切片をＣとするとＣ（０、６）
△ＡＣＯ：△ＡＰＯ＝６：10/３＝⑨：⑤
△ＡＣＰ＝⑨－⑤＝④

ｘ座標の差からＢはＡＣの中点なので、△ＢＣＰ＝△ＡＢＰ＝②
Ｓ（△ＡＢＰ）：Ｔ（△ＡＰＯ）＝２：５

大問３（確率・データの活用）

（１）①　39.5％

１回目が２回目より大きくなる。
●（３→２）
３は２個、２は３個だから、２×３＝６通り
●（５→２or３）
５は１個、２or３は５個だから、１×５＝５通り
計11通り、全体は６×６＝36なので確率は11/36。

②　32.2％！
１回目が２回目より小さくなる。
【Ｐ】
（３→５）
２×１＝２通り
（２→３or５）
３×３＝９通り
計11通り、確率は11/36。
【Ｑ】
Ｘで何を出そうとも、Ｙで６をひけば条件を満たす。
Ｙだけを考えればいい。６をひく確率は１/３。
11/36＜１/３だから、確率が大きいのはＱ。
Ｑ、１/３

＠別解＠
【Ｐ】は余事象で求めることもできる。
前問より、１回目が大きくなる場合は11通り。
同数は２が３×３＝９通り、３が２×２＝４通り、５が１×１＝１通りで計14通り。
１回目が小さくなる場合は、36－（11＋14）＝11通り

（２）①　65.4％

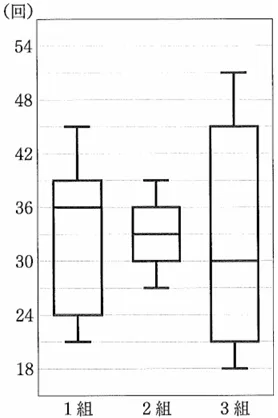
範囲＝最大値－最小値
１目盛りは３回。
１組の範囲は、45－21＝24回

②２点…55.2％、１点…22.0％
１組は中央値（36回）、２組は最小値（27回）、３組は最大値（51回）が最も大きい。
きちんと数値を示せば、本問はいずれも正解になる。
もっとも、最小値・最大値は極端な場合もあるので、実際はデータ全体を捉える中央値が無難かもしれない。

大問４（方程式）

（１）①ア　80.8％
22÷２＝11列

イ　58.7％
２人組が２ｘ人、３人組が３ｙ人で合計25人だから、
２ｘ＋３ｙ＝25

②　33.8％
【２×11＋３×１＝25】
２と３を交換する。２を－３個、３を＋２個していくと、
【２×８＋３×３＝25】
【２×５＋３×５＝25】
【２×２＋３×７＝25】
以上４組。

（２）　25.9％！

【Ⅰ～Ⅲ】より、どの階にも４人部屋と６人部屋は同数ずつある。
ある階の６人部屋をｘ室とすると、４人部屋は３ｘ室。
定員で等式を立てる。
【Ⅳ】より、１つの階における定員の合計は、432÷４＝108名
４×３ｘ＋６ｘ＝108
ｘ＝６
６人部屋は６室、４人部屋は６×３＝18室。
定員４名…18部屋　定員６名…６部屋

大問５（空間図形）

（１）　63.2％
６×６×12÷３＝144ｃｍ³

（２）①　31.0％！

立体Ｘ：四角錘Ｏ―ＡＢＣＤの相似比は、８：12＝２：３
体積比は相似比の３乗→立体Ｘ：四角錘＝２³：３³＝⑧：㉗
立体Ｘの体積は、144×⑧/㉗＝128/３ｃｍ³

②　8.0％!!

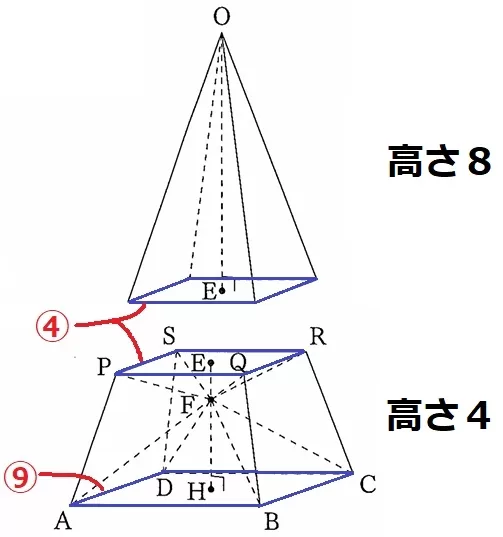
比で立式を試みる。
面積比は相似比は２乗→四角形ＰＱＲＳ：四角形ＡＢＣＤ＝④：⑨
右図は正面からみた様子。立体全体が前後で対称なので、
体積比を面積比に置き換えると、△ＦＡＢ＋△ＦＰＱ＝△ＯＰＱ
ＦＨ＝ｘとすると、△ＦＰＱの高さは４－ｘなので、
⑨ｘ＋④（４－ｘ）＝④×８　←÷２を除去しています。同一比なので〇を消す
５ｘ＝16
ｘ＝16/５
ＦＨ＝16/５ｃｍ

大問６（平面図形）

（１）３点…28.9％！、２点…5.4％、１点…17.9％、無記入…28.9％
△ＡＢＣ∽△ＦＤＣの証明。

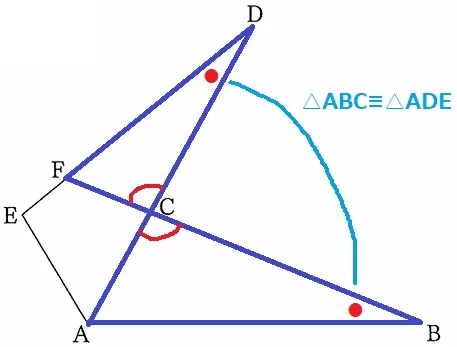
対頂角＋△ＡＢＣ≡△ＡＤＥの対応する角で２角相等の∽。

（２）　17.0％！

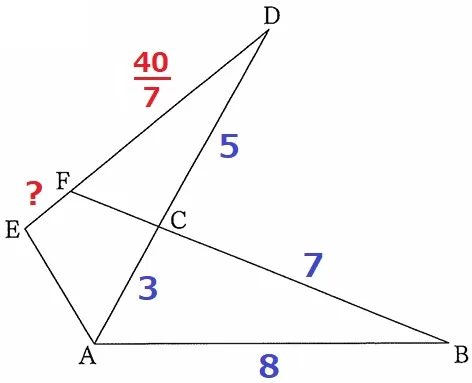
ＥＦ＝ＥＤ－ＦＤ
ＦＤは△ＦＤＣの１辺だから、前問の相似を使う。
ＡＤ＝ＡＢ＝８ｃｍ
ＣＤ＝８－３＝５ｃｍ
△ＡＢＣ∽△ＦＤＣより、ＦＤ＝８×５/７＝40/７ｃｍ

ＥＤ＝ＣＢ＝７ｃｍ
ＥＦ＝７－40/７＝９/７ｃｍ

（３）　2.0％!!

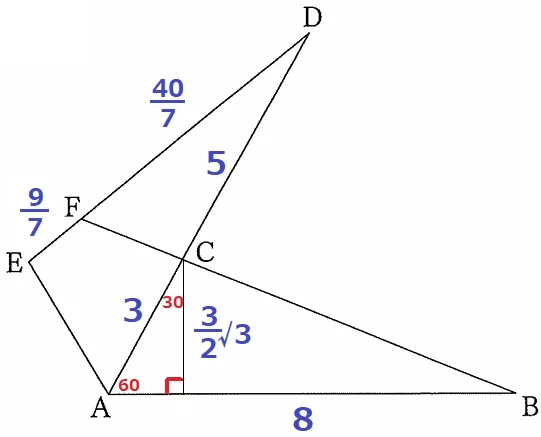
面積を求めるので高さが必要。ここで60°を用いる。
△ＡＢＣの回転移動で対応するＡＢとＡＤがなす角である∠ＤＡＢ＝60°
ＣからＡＢに垂線をひく。
30°－60°－90°の直角三角形の辺の比から、△ＡＢＣの高さは３×√３/２＝３√３/２ｃｍ
合同より△ＡＤＥも同様。

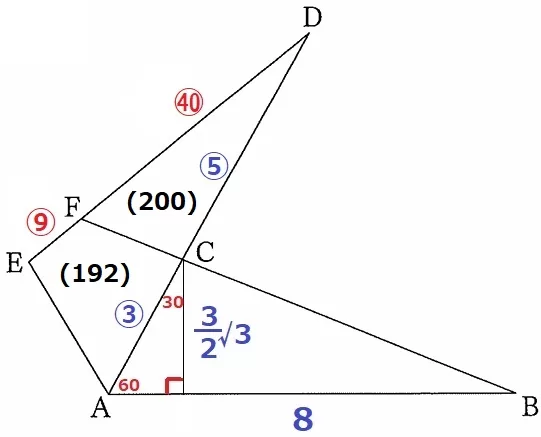
隣辺比で面積比を算出する。
△ＡＤＥ：△ＣＤＦ＝㊾×⑧：㊵×⑤＝392：200
四角形ＡＣＦＥの面積比は、392－200＝192
したがって、８×３√３/２÷２×192/392＝144√３/49ｃｍ²