問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
２－16
＝－14
（２）
７/３＋２/９×（－３）
＝７/３－２/３
＝５/３
（３）
（６ａ2ｂ－４ａｂ2）÷２ａｂ ←分配法則
＝６ａ2ｂ÷２ａｂ－４ａｂ2÷２ａｂ
＝３ａ－２ｂ
（４）
２（ａ＋７ｂ）－８ｂ
＝２ａ＋６ｂ ←ここで代入
＝２×（－５）＋６×１/６
＝－10＋１
＝－９
（５）
ｘ2－10ｘ＋21
＝（ｘ－３）（ｘ－７）
（６）
反比例はｘとｙの積が比例定数ａで一定。
ａ＝－２×９＝－18
ｙ＝－18/ｘ
（７）
７/√７＝√７
３＝√９
√７＜√９＜√10だから、７/√７＜３＜√10
エ
（８）
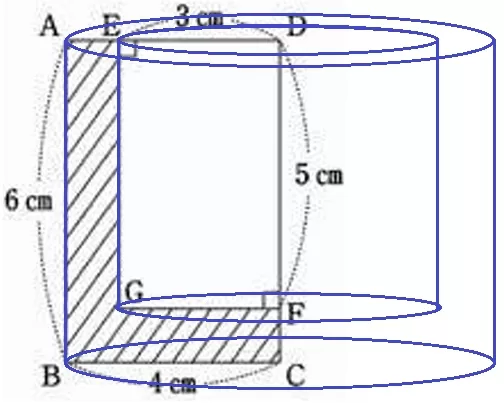
半径４ｃｍ高さ６ｃｍの円柱から、半径３ｃｍ高さ５ｃｍの円柱をくり抜く。
４×４×π×６－３×３×π×５
＝96π－45π＝51πｃｍ3
大問２（小問集合２）
（１）①
和が６となる組み合わせは、
（ａ、ｂ）＝（１、５）（２、４）（３、３）（４、２）（５、１）
計５通り、全体は６×６＝36通りだから確率は５/36。
②
分母のａで場合分け。
ａ＝１→必ず整数になる。ｂ＝１～６
ａ＝２→奇数を選ぶ。ｂ＝１・３・５
ａ＝３→ｂ＝２・５
ａ＝４→ｂ＝３
ａ＝５→ｂ＝４
ａ＝６→ｂ＝５
計14通りで、確率は14/36＝７/18
（２）①
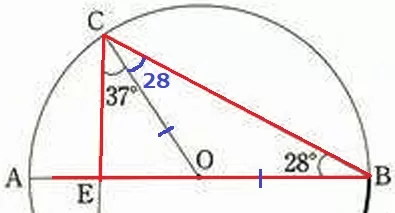
半径から△ＯＢＣは二等辺→∠ＯＣＢ＝28°
△ＣＥＢで外角定理、∠ＡＥＣ＝37＋28×２＝93°
②
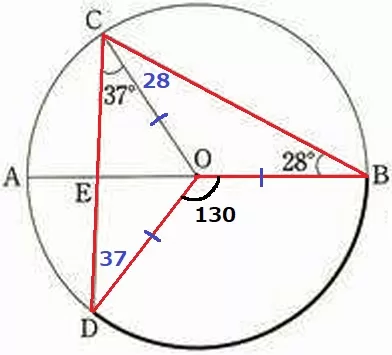
中心角である∠ＢＯＤが知りたい。
半径より△ＯＣＤも二等辺→∠ＯＤＣ＝37°
ブーメランの３つ角の和が股の角、∠ＢＯＤ＝（37＋28）×２＝130°
弧ＢＤの長さは、６π×130/360＝13/６πｃｍ
（３）①
ｙ＝１/２ｘ2にｘ＝４を代入→Ａ（４、８）
Ｂはｙ軸についてＡと対称だからＢ（－４、８）
②
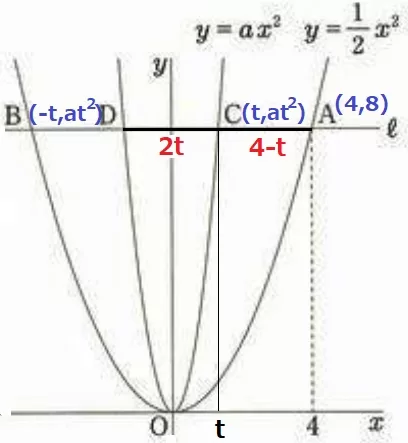
Ｃのｘ座標をｔとする。Ｃ（ｔ、ａｔ2）Ｄ（－ｔ、ａｔ2）
ＡＣ＝４－ｔ
ＣＤ＝ｔ－（－ｔ）＝２ｔ
４－ｔ＝２ｔ
ｔ＝４/３
Ｃのｙ座標で等式を立てる。
ａｔ2＝（４/３）2ａ＝16/９ａ＝８
ａ＝９/２
（４）①
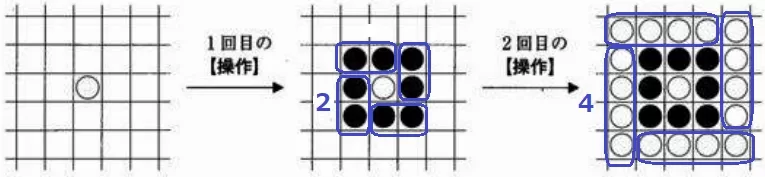
方陣算。上図のように４つのグループにまとめる。
１回目は２個ずつ、２回目は４個ずつ…。
３回目は６個ずつ、４回目は８個ずつだから８×４＝32個
②ア
ｎ回目は２ｎ個ずつのグループになる。
新たに置いた碁石は、２ｎ×４＝８ｎ＝88
ｎ＝11
11回目
イ
黒の碁石は奇数回目で置く→１・３・５・７・９・11回目
奇数回目の１グループの合計を一括して求める。
11は６番目の奇数だから、１＋３＋５＋７＋９＋11＝６2＝36個
１グループの合計は、36×２＝72個
４グループずつあるから、全部で72×４＝288個
大問３（データの活用・数量変化）
（１）①
最小値が最も小さいＣ組。
②
説明問題。
40人の中央値は20番目と21番目の平均。
どのクラスも中央値は340秒未満→各組に少なくとも20人は340秒以内である。
４組全体では少なくとも80人は340秒以内である。
（２）①
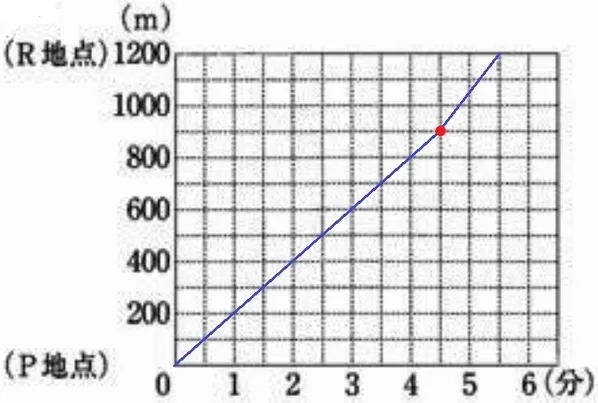
洋平はＰＱ間を900ｍ÷分速200ｍ＝4.5分、ＱＲ間を300ｍ÷分速300ｍ＝１分で走る。
０→（4.5、900）→（5.5、1200）を結ぶ。
②ア
明は1200ｍ÷分速250ｍ＝４分48秒走る。
洋平とすれ違うのはＱ地点からＰ寄り。
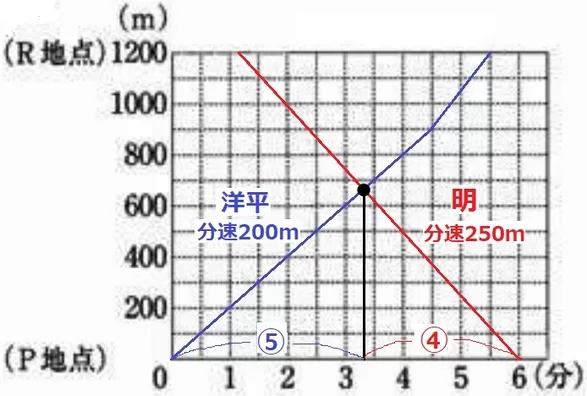
中受の戦法を使います。
速さの比は洋平：明＝200：250＝４：５
時間は逆比で、洋平：明＝⑤：④
Ｐ地点から２人が出会う地点までの距離を洋平は⑤、明は④の時間がかかった。
⑨＝６分なので、出会う時間⑤は６×⑤/⑨＝10/３＝３・１/３分＝３分20秒後
イ
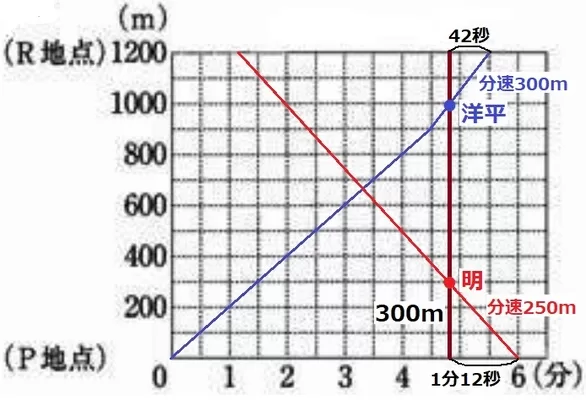
300ｍ÷分速250ｍ＝６/５分＝１分12秒
明はＰ地点到着から１分12秒前に300ｍ手前にいた。
洋平は明より30秒前にＲ地点へ到着するので、Ｒ到着から１分12秒－30秒＝42秒前
このとき、洋平は分速300ｍで走っている。
Ｒ地点までの距離は、300ｍ×42秒/60秒＝210ｍ
Ｐ地点までの距離は、1200－210＝990ｍ
大問４（平面図形）
（１）
Ｄ、ＥはそれぞれＡＢ、ＡＣの中点。
中点連結定理より、ＤＥ＝ＢＣ÷２＝10÷２＝５ｃｍ
（２）
△ＡＤＦ≡△ＤＢＥの証明。
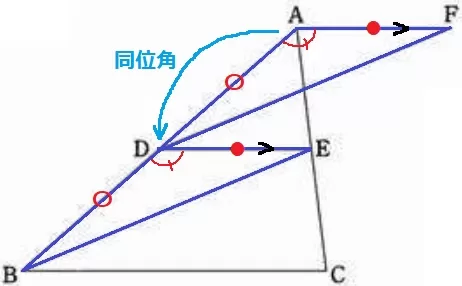
仮定から、ＡＦ＝ＤＥ
ＤはＡＢの中点だから、ＡＤ＝ＤＢ
ＡＦ//ＤＥの同位角より、∠ＦＡＤ＝∠ＥＤＢ
２辺とあいだの角が等しいから合同。
（３）①
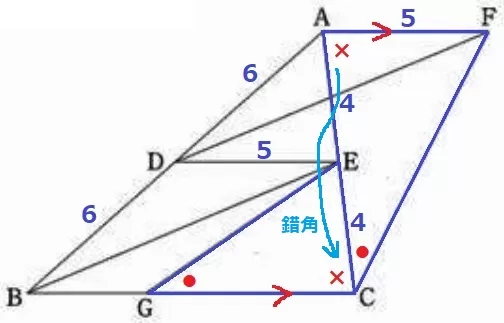
仮定の∠ＣＧＥ＝∠ＡＣＦ（●）
ＡＦ//ＧＣの錯角で、∠ＥＣＧ＝∠ＦＡＣ（×）
２角相等で△ＣＧＥ∽∠ＡＣＦ
ＣＧ：ＡＣ＝ＥＣ：ＦＡ
ＣＧ＝８×４/５＝32/５ｃｍ
②
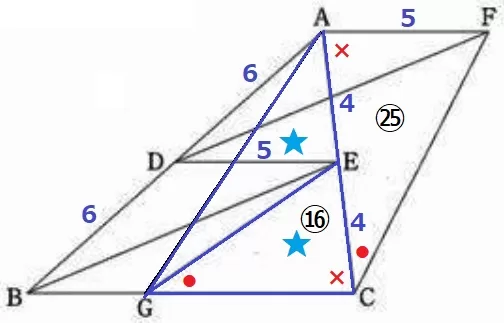
ＡＥ＝ＥＣより、△ＡＧＥと△ＣＧＥは等積である。
前問より、△ＣＧＥ∽△ＡＣＦの相似比は４：５→面積比は２乗して⑯：㉕
△ＡＣＦの底辺はＡＦ＝５ｃｍと出ているので、高さがわかればすべて求まる。
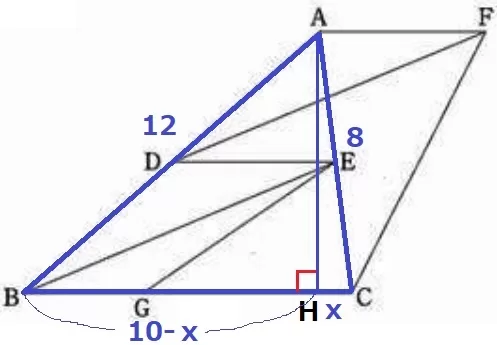
３辺の長さが判明している△ＡＢＣに着目する。
Ａから垂線をおろして足をＨとし、ＨＣ＝ｘとおく。
ＢＨ＝10－ｘ
【ＡＢ2－ＢＨ2＝ＡＨ2＝ＡＣ2－ＨＣ2】
122－（10－ｘ）2＝８2－ｘ2
144－100＋20ｘ－ｘ2＝64－ｘ2
20ｘ＝20
ｘ＝１
△ＡＨＣで三平方→ＡＨ＝３√７ｃｍ
したがって、△ＡＧＥ（△ＣＧＥ）の面積は、５×３√７÷２×⑯/㉕＝24√７/５ｃｍ2
大問１
配点26点。
（７）根号で大小関係を比較する。
大問２
（１）②分子のｂではなく、分母のａで整理する。
（２）②ＤＯに補助線をひけるかどうか。
（４）②ア：１グループの個数はｎの２倍である。
イ：奇数回目だけを抜き出して、１グループの合計を４倍する。
連続する〇番目までの奇数の和は、〇×〇で求められる。
大問３
（１）①『数値が小さい方が速い記録』とヒントがある。
（２）ア：高校受験の正攻法は２直線の交点座標を求める。
イ：どんな情報が欲しいか、それから何がいえるか。手順を追っていく。
まず、明が300ｍ手前にいたときの時間を求める。
これは先にゴールに着いた洋平では何秒前か→洋平の場所を求める。
大問４
（２）変わった位置関係だが、証明の方針は立てやすい。
（３）①ＣＧを１辺とする△ＣＧＥと∽にあたる三角形を探す。
等角の仮定から見つけやすい。
②（１）でＥがＡＣの中点であることに触れている。
ここから求めにくい場所にある△ＡＧＥを先ほどの△ＣＧＥに置き換えることができる。
高さを求めるには三平方を用いたテクニックを要する。
前問でＣＧ＝32/５ｃｍと出したので、32/５×３√７/２÷２＝24√７/５ｃｍ2と出してもいい。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
宮崎県のラス問は毎年メネラウスとかチェバとか中線定理とか使わないと無理だろ！といった感じですが、今年はそんなこともなく受験生の努力が報われそうな形式になっていてよかったです。同じように大分県のラス問もここ数年相当易化しており何が起きたんだ?と感じています。{良い変化だとは思いますが、難問も見たいんです(´ω`)}
コメントありがとうございます。新生活はいかがでしょうか。
気持ちはわかります（笑）昨年の宮城は平均ダダ下がりだったので、揺り戻しで易しくしたのだと思います。
最後の大問で平面をポッと出すところは妙に期待しちゃいます。山形とか奈良滋賀とか。
しかし、あまりやりすぎると苦情も入るようです。私も講評で何度か書いたことが(;^ω^)