平均19.6点（前年比；－2.8点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）ア
４－11
＝－７
イ
４（２ｘ＋ｙ）－３（ｘ－３ｙ）
＝８ｘ＋４ｙ－３ｘ＋９ｙ
＝５ｘ＋13ｙ
ウ
（－６ｘｙ3）÷（－２ｘｙ）
＝３ｙ2
エ
√27－√12
＝３√３－２√３
＝√３
（２）
ｘ2－３ｘ－40
＝（ｘ＋５）（ｘ－８）
（３）
３ｘ2＋ｘ－１＝０
解の公式を適用して、ｘ＝（－１±√13）/６
（４）
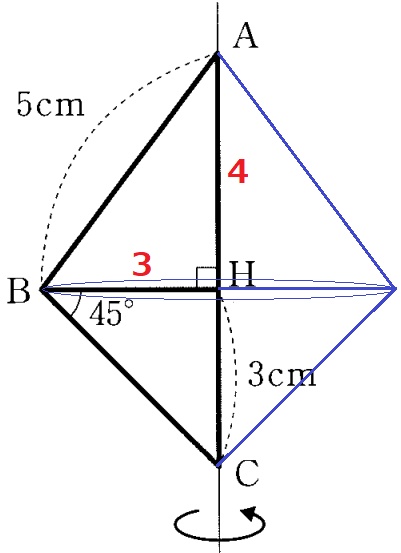
△ＢＣＨは直角二等辺→ＢＨ＝３ｃｍ
△ＡＢＨは３：４：５の直角三角形→ＡＨ＝４ｃｍ
回転体は底面が半径３ｃｍ、高さ合計が７ｃｍの円錐である。
３×３×π×７÷３＝21πｃｍ3
（５）
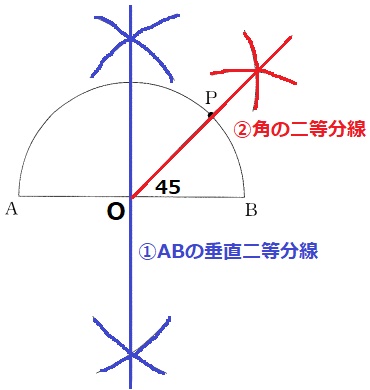
円の中心をＯとすると、弧ＡＰ：弧ＰＢ＝∠ＡＯＰ：∠ＰＯＢ＝③：①
∠ＰＯＢ＝180×①/④＝45°
①ＡＢの垂直二等分線。
②90°を二等分する。半円の弧との交点がＰ。
（６）
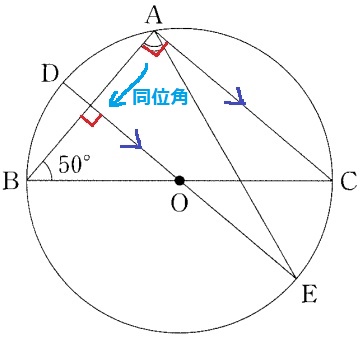
半円の弧に対する円周角より、∠ＢＡＣ＝90°
ＡＣ//ＤＥの同位角で90°を移す。
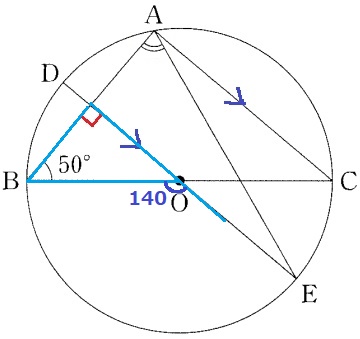
水色の三角形で外角定理→∠ＢＯＥ＝50＋90＝140°
∠ＢＡＥは弧ＢＥに対する円周角なので、∠ＢＡＥ＝140÷２＝70°
（７）
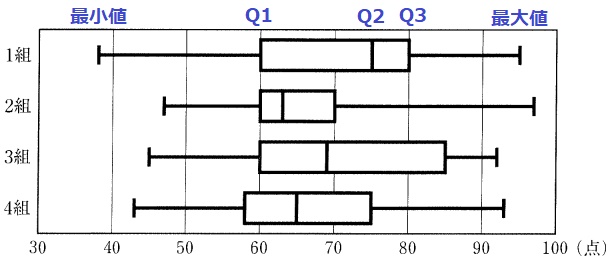
ア：最大値が最も大きい２組に最高点者がいる。〇
イ：×印などで平均値を示す箱ひげ図もあるが、本問にはない。×
ウ：四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）
箱が最も長いのは３組。×
エ：箱の区間は中央値（Q2）を真ん中にデータ全体の約50％。
１組も２組も全体は30人で同じだから、箱の区間のデータの個数は同じ。×
Q1は下位15人の真ん中→８番目、Q3は上位15人の真ん中→23番目、23－８＋１＝16個
オ：２組のQ3（上から８番目）が70点→70点以上は８人以上いる。〇
ア・オ
大問２（方程式）
（１）ア
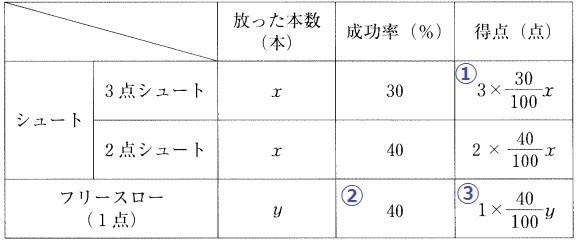
①３点シュートｘ本は成功率30％→３×30/100ｘ
②フリースローの成功率は２点シュートと同じ→40
③１点のフリースローｙ本は成功率40％→１×40/100ｙ
ウ
イ
３点と２点をｘ本ずつ、１点をｙ本放った。
シュートの合計本数で等式。
２ｘ＋ｙ＝85
もう１つは合計得点で等式。表を活用する。
３×30/100ｘ＋２×40/100ｘ＋１×40/100ｙ＝61
④２ｘ＋ｙ、⑤３×30/100ｘ＋２×40/100ｘ＋１×40/100ｙ
ウ
２ｘ＋ｙ＝85 …①
３×30/100ｘ＋２×40/100ｘ＋１×40/100ｙ＝61 ←10倍して整理
17ｘ＋４ｙ＝610 …②
②－①×４をすると、９ｘ＝270
ｘ＝30
留意点は、３点シュートを放った本数が30本。
成功率は30％なので、実際に成功した３点シュートは30×30％＝９本
（２）ア
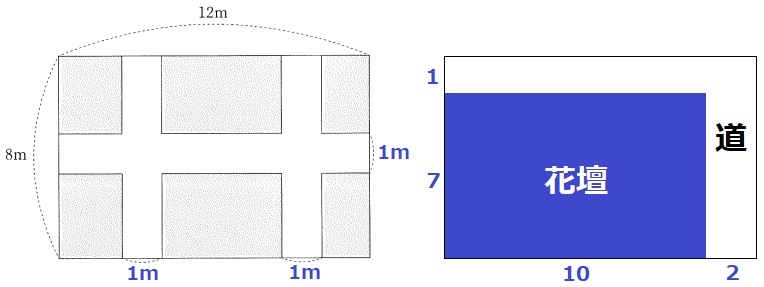
花壇を隅に寄せる。
通路の面積は、８×12－７×10＝26ｍ2
イ
道路の幅をｘｍとして、前のように花壇を寄せると、
花壇の面積は、（８－ｘ）（12－２ｘ）
＝96－16ｘ－12ｘ＋２ｘ2
＝２ｘ2－28ｘ＋96
通路の面積は、96－（２ｘ2－28ｘ＋96）
＝－２ｘ2＋28ｘｍ2
ウ
通路と花壇の面積が等しい→通路の面積は、96÷２＝48ｍ2
－２ｘ2＋28ｘ＝48
２ｘ2－28＋48＝０ ←÷２
ｘ2－14＋24
＝（ｘ－２）（ｘ－12）＝０
ｘ＝２、12
ここでｘの条件を調べる。
ｘは長さなので０より大きい。
また、花壇の長さも０より大きい。
８－ｘ＞０→ｘ＜８
12－２ｘ＞０→２ｘ＜12→ｘ＜６
範囲を絞ると０＜ｘ＜６だから、ｘ＝２
２ｍ
大問３（関数）
（１）
ｙ＝ａｘ2にＡ（－２、－２）を代入。
－２＝４ａ
ａ＝－１/２
（２）
ｙ＝ｂ/ｘにＢ（６、２）を代入。
２＝ｂ/６
ｂ＝12
（３）
ｙ＝－１/２ｘ2にｘ＝－４を代入。
ｙ＝－１/２×（－４）2＝－８
Ｃ（－４、－８）
（４）
同様にＤ座標を求める。
Ｃ（－４、－８）→Ｄ（２、－２）
右に６、上に６だから、傾きは６/６＝１
切片はＤから左に２、下に２移動して、－２－２＝－４
ｙ＝ｘ－４
（５）
ｙ＝12/ｘ（ｘ＞０）が通る格子点を数える。
（１、12）（２、６）（３、４）（４、３）（６、２）（12、１）の６個。
（６）
△ＡＢＣを変形する。
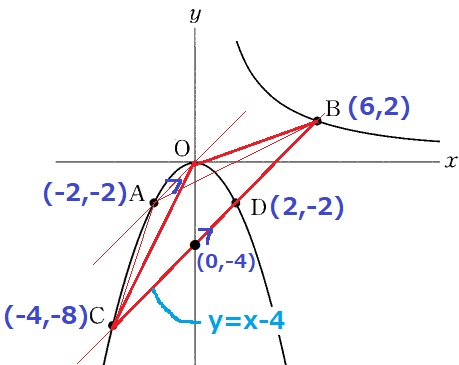
ｙ＝ｘ－４にｘ＝６を代入するとｙ＝２
→ＢはＣＤ上にある。
Ａを通るＢＣに平行な線（傾き１）をひくとOを通過する。
等積変形より、△ＡＢＣ＝△ＯＢＣ
△ＯＢＣは幅10、高さ４だから、10×４÷２＝20
（７）
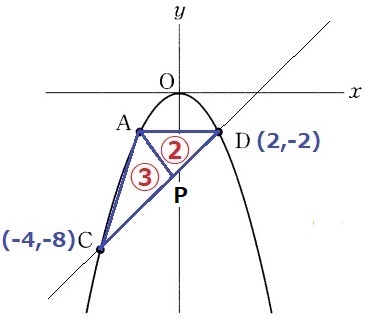
△ＡＣＰ：△ＡＤＰ＝ＣＰ：ＤＰ＝③：②
ＰはＣよりＤに近い。
１つ目はＰがＤの左にある場合。
ＣとＤのｘ座標の差は６。Ｐのｘ座標は、２－６×②/⑤＝－２/５
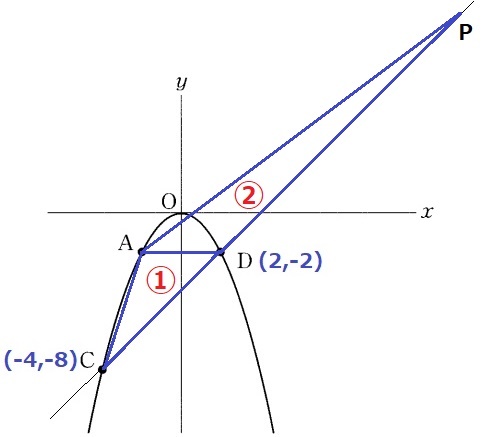
もう１つはＰがＤの右にある場合。
ＣＰ：ＤＰ＝③：②→ＣＤ：ＤＰ＝①：②
Ｐのｘ座標は、２＋６×②＝14
ｘ＝－２/５、14
大問４（平面図形）
（１）
△ＡＢＣで三平方→３√３ｃｍ
（２）
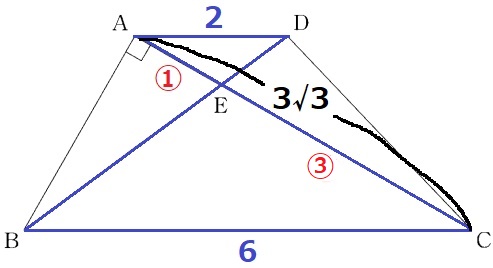
△ＡＤＥ∽△ＣＢＥより、ＡＥ：ＥＣ＝①：③
ＣＥ＝３√３×③/④＝９√３/４ｃｍ
（３）ア
△ＤＦＧ∽△ＡＣＧの証明。
対頂角とＡＣ//ＦＤの錯角→２角相等で∽。
イ
前問の三角形の面積比を求める。相似比がわかればいい。
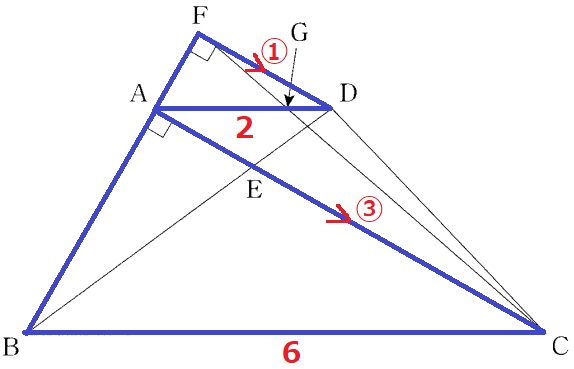
ＡＣ//ＦＤを手掛かりに２角相等で△ＡＤＦ∽△ＢＣＡ
ＦＤ：ＡＣ＝ＡＤ：ＢＣ＝①：③
面積比は相似比の２乗→△ＤＦＧ：△ＡＣＧ＝①2：③2＝１：９
△ＡＣＧ＝△ＤＦＧ×９＝９Ｓ
ウ
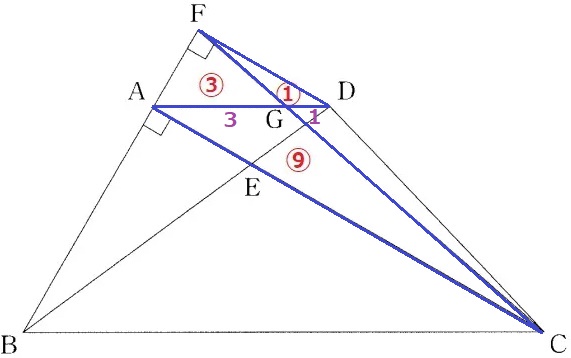
△ＤＦＧなので前問の面積比を使う。
△ＤＦＧ∽△ＡＣＧより、△ＤＦＧ：△ＡＣＧ＝①：⑨
相似比のＡＧ：ＧＤ＝３：１から、△ＡＧＦ＝①×３＝③
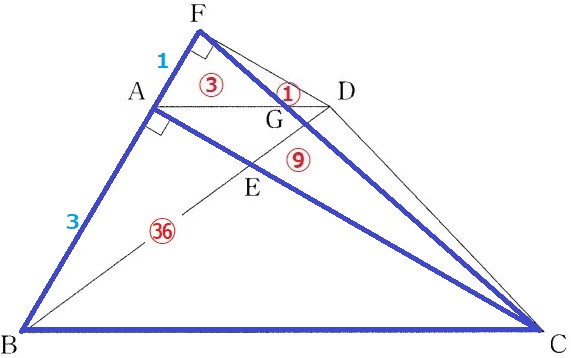
前問で触れた△ＡＤＦ∽△ＢＣＡの相似からＦＡ：ＡＢ＝１：３
△ＢＣＡ＝△ＡＣＦ（⑫）×３＝㊱
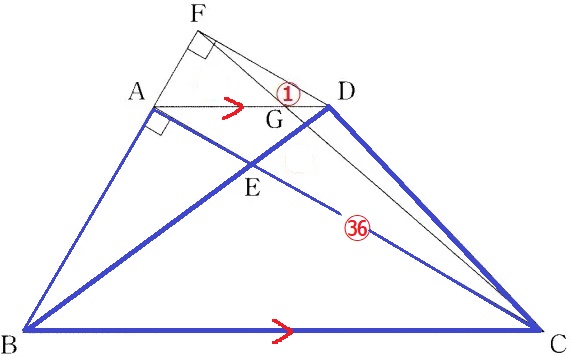
ＡＤ//ＢＣより、△ＢＣＡ＝△ＢＣＤ＝㊱
Ｓ（△ＤＦＧ）：Ｔ（△ＢＣＤ）＝１：36
大問５（確率・規則）
（１）ア
【２】【０】を出す→時計回りに270°（＝反時計回りに90°）
エ
イ
取り出したカードは戻さない。
１回目に０を出さない→４枚中３枚
２回目も０を出さない→残り３枚中２枚
３/４×２/３＝１/２
ウ
操作２回で文字を左向きにする→アの【０】【２】しかない。
【２】が２枚あることに注意！ＡとＢで区別する。
【０】【２Ａ】と【０】【２Ｂ】の２通り。
全体は４枚から２枚を選ぶ→4Ｃ2＝６通り
確率は、２/６＝１/３
エ
１回目に０を出すと逆さになってしまうので、１回目の２か４で場合分け。
●１回目に２→２回目は２以外を出す。
２/４×２/３＝１/３
●１回目に４→２回目は４以外を出す。
２回目は何を引いてもいいので、１回目の１/４。
合計して、１/３＋１/４＝７/12
（２）ア
奇数を互い違いに足していく。
図形５のＸは15。
イ
図形６のＸ－Ｙ＝15－21＝－６
ウ
Ｘ－Ｙの値は図形の番号と対応しており、＋と－が交互に繰り返す。
Ｘ－Ｙ＝９→図形９のＸを求めればいい。
奇数番目と偶数番目で様子が異なるので、奇数番目だけに着目する。
図形１→１×１＝１
図形３→３×２＝６（３は２番目の奇数）
図形５→５×３＝15（５は３番目の奇数）
奇数ｎがｍ番目の奇数とすると、図形ｎのＸ＝ｎｍ
９は５番目の奇数だから、図形９のＸ＝９×５＝45
エ
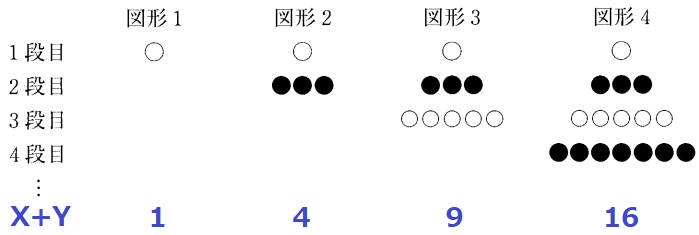
連続する奇数和は、奇数ｍ番目の２乗。
255＝152→図形15を求める。
15は、（15＋１）÷２＝８番目の奇数
Ｘ＝15×８＝120
Ｙ＝225－120＝105
Ｘ…120、Ｙ…105
小問数が多い。わかる問題は早めに解決したい。
大問１
（４）上下に有名三角形。高さ合計で一括処理する。
（６）平行をどう活用するか。
ゴールの∠ＢＡＥから遡って、どこの角を調べればいいか探る。
大問２
（１）３つの要素とそれぞれに成功率がつく。
やや複雑な条件だが、最初をミスるとドミノ倒しなので落ち着いて対処したい。
表をもとに立式。ウ：放った本数を文字に置いていることに注意！
（２）イ：計算ミスをしないように。
ウ：先に道路の面積を求めておくと計算が楽。
大問３
（５）までは取りたい。
（６）Ｂを通るＣＯに平行な線を引き、Ｂをｘ軸に移してもいい。
ＣＯは傾き２→Ｂの移動先は（５、０）→５×８÷２＝20
（７）ＰがＣ寄りかＤ寄りかを確定しておく。
Ｄ寄りなので、Ｄの左か右で２通りある。
大問４
（３）イ：別の相似に乗り換える。
ウ：今までの解答をフル活用する。
あらかじめ、△ＢＣＤを△ＢＣＡに等積変形しておくと良い。
大問５
（１）イ：積の法則。樹形図で調べる際は２枚の【２】を区別する。
エ：ここも立式が苦手な人は樹形図で対処できる。
（２）ウ：図形の番号と奇数番目のＸの法則を見つける。
×１、×２、×３…なので、図形９は×５。これは９が奇数の５番目だから。
エ：連続する奇数和は平方数になる。
図形15は奇数。前問の法則からＸが先に求まる。
公立高校入試解説ページに戻る
コメント