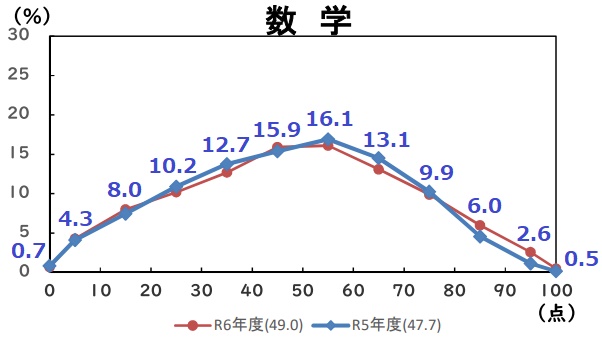
平均48.8点(前年比;+1.4点)
問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1)① 94.4%
(-1)+(-5)
=-1-5
=-6
② 90.5%
7+18÷(-3)
=7-6
=1
③ 81.6%
√6×√3-√2
=3√2-√2
=2√2
(2) 74.2%
素因数分解…素数の積であらわす。
70=2×5×7
(3) 81.2%
比例。
1mで30g→比例定数a=30
y=30x
(4) 70.7%
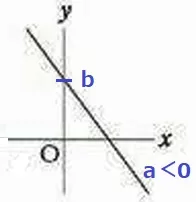
傾きは右下だからaは負の数。
切片bの値はy>0で正の数。
①…ウ、②…ア
(5) 65.7%
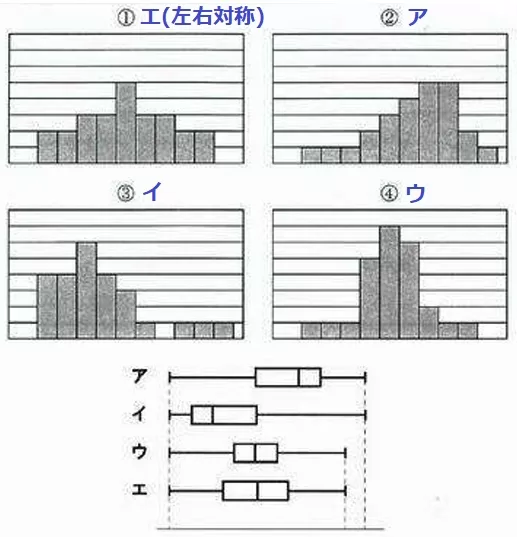
最大値が小さい①・④はウ・エのどちらか。
①は左右対称だからエ。
④も微妙に対称的だが、中央部分にデータが集中しているため、
四分位範囲(第3四分位数-第1四分位数;箱の長さ)がエよりも小さいウ。
残りで右に寄っている②がア、左に寄っている③がイ。
①…エ、②…ア
(6) 55.6%
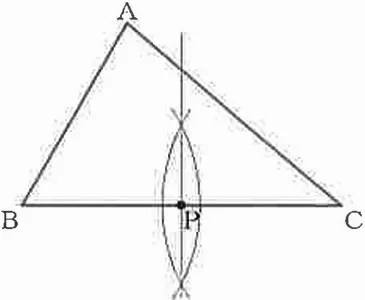
△ABP=△ACPでPはBC上にある→PはBCの中点。
BCの垂直二等分線とBCとの交点がP。
大問2(文字式)
(1)① 69.8%
勇太の求め方によると、白は2a+4a-4=6a-4本。
a=6を代入、6×6-4=32本
② 37.1%
別の求め方をつくる。白の区切り方を変えればいい。
指定された通りに式を書く。整理するといずれも6a-4になる。
(2) 29.4%!
勇太の考えがわかりやすい。
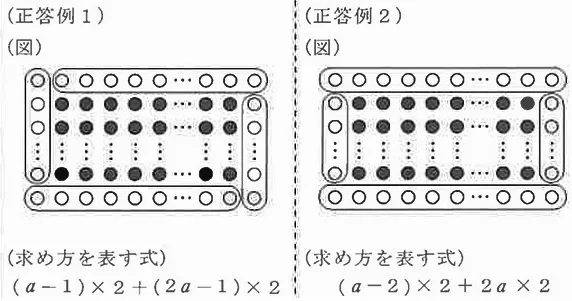
全体(白+赤)は、2a2=242
a2=121
a>0だから、a=11
両端は白なので、赤の縦は11-2=9本、横は11×2-2=20本。
赤は9×20=180本
大問3(関数)
(1)① 79.8%
y=x2にx=3を代入。
y=9
② 55.5%(部分点11.0%)
答案では求め方も書く。
B(-2、4)→A(3、9)
右に5、上に5だから、傾きは5/5=1
切片はBから右に2、上に2移動して、4+2=6
y=x+6
(2) 21.9%!(部分点10.2%)
答案では求め方も書く。
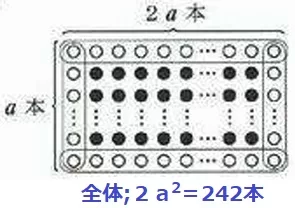
各座標をtで表すとこうなる。
△PQRが直角二等辺→PQ=PQ
2t=3/2t2 ←2倍
4t=3t2
3t2-4t
=t(3t-4)=0
t>0だから、t=4/3
大問4(平面図形)
(1) 20.5%!
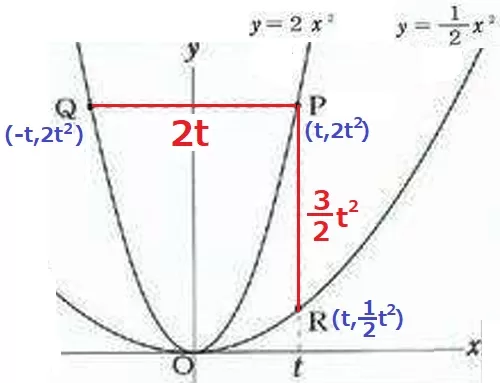
適当な菱形を描いて調べる。
横長の菱形の中には横長の長方形ができる。
『ことがらが成り立たないもの』を選ぶのでア・ウ。
@@
中に正方形ができるのは、外も正方形のときだけである。
(2)① 7.6%!!(部分点5.0%)
四角形PQRSが平行四辺形である証明。
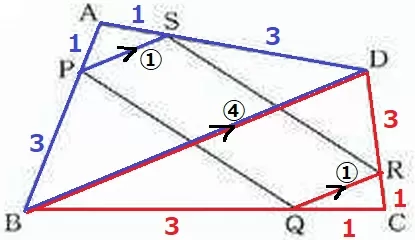
BDに補助線を引く。
AP:PB=AS:SDから、PS//BD
CQ:QB=CR:RDから、QR//BD
→PS//QR
△APS∽△ABDの相似比は、PS:BD=1:4
△CQR∽△CBDの相似比は、QR:BD=1:4
→PS=QR
1組の対辺が平行かつ長さが等しいので、四角形PQRSは平行四辺形である。
@@
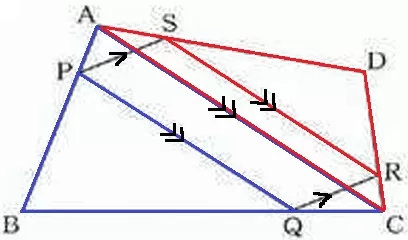
正答例2はPS//QRを指摘したうえで、ACに補助線をひき、
PQ//SRより2組の対辺がそれぞれ平行→平行四辺形
② 9.4%!!
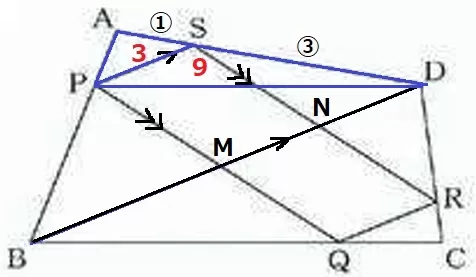
辺の比を利用して下側の面積を求めにいく。
PDに補助線。
AS:SD=△APS:△SPD=①:③
△SPDの面積は、3×③=9cm2
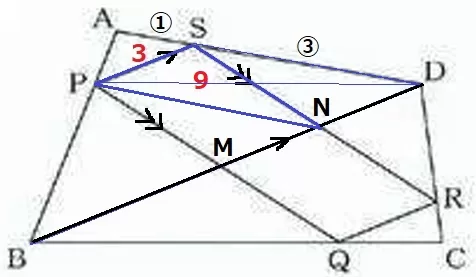
PS//BDの等積変形で、△SPD=△SPN=9cm2
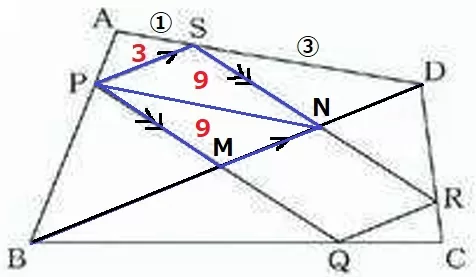
四角形PMNSは2組の対辺が平行だから平行四辺形。
対角線PNは2等分するので、四角形PMNSの面積は9×2=18cm2
大問5(総合問題)
(1)① 54.7%
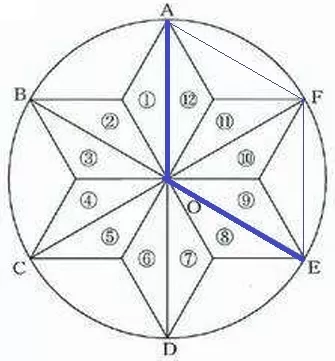
①と⑨の対応する辺(AO→EO)だけを見る。
時計回りの∠AOEを求めればいい。
△AOFと△FOEは正三角形→∠AOE=60×2=120°
② 42.5%(部分点0.2%)
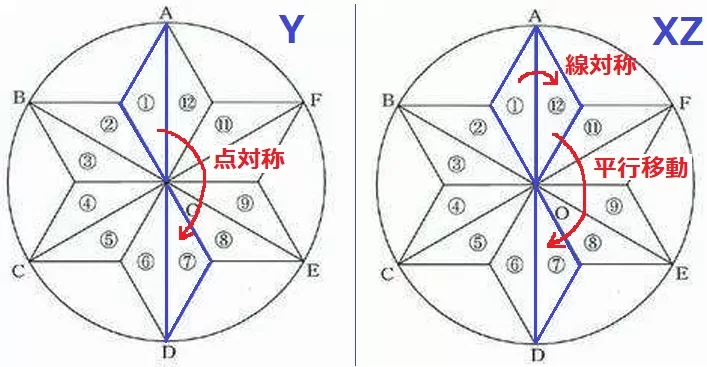
①→⑦に移動する経路を考える。
点対称で①→⑦(Yだけ表)
ADの線対称と平行移動で①→⑫→⑦(XZだけが表)
2通りしかない。
全体は23=8通りなので、確率は2/8=1/4
(2) 9.3%!!(部分点6.7%)
答案では求め方も書く。
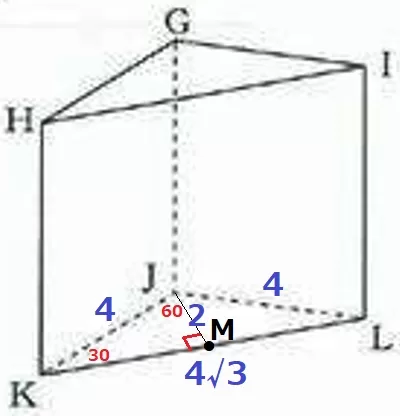
△JKLは頂角120°の二等辺三角形。
KLの中点をMとする。
△JKMの内角は30°―60°―90°→辺の比が1:2:√3の直角三角形。
JM=2cm、KL=KM×2=2√3×2=4√3cm
△JKLの面積は、4√3×2÷2=4√3cm2
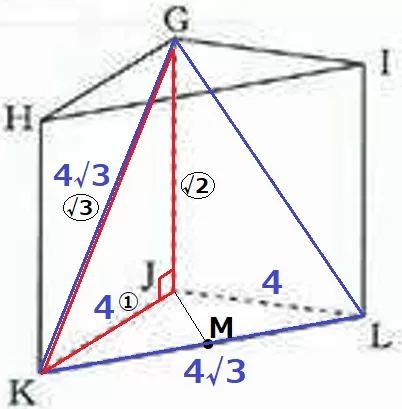
あとは三角柱の高さがわかれば体積が求まる。
△GKLは正三角形なので、GK=KL=4√3cm
GK:KJ=4√3:4=〇√3:①
△GKJの辺の比で三平方→GJ=〇√2=4√2cm
三角柱の体積は、4√3×4√2=16√6cm3
●講評●
前半は易問が多い。
大問1
配点35点。いずれも基本問題。
(5)四分位数の算出もなく、選びやすかった。
大問2
(1)②四隅をどう処理するか。
(2)例題の勇太を手掛かりにすると難しくはない。
大問3
(2)tを用いた座標問題。公立高校入試では頻出。
他県ではもう少し複雑な設定で出題される。
大問4
(1)正方形が成り立つとすべて成り立つので、長方形か菱形のいずれか。
(2)ポイントは対角線。経験の差が出やすい。
A方面とC方面で1:3の∽があり、共通辺BDからPS=QRが導ける。
(3)台形PBDSで上底+下底の和でもいけるが、
端に寄せた三角形を等積変形で中央に移すと処理が楽になる。
大問5
(2)そんなにパターンもないので、自信がなかったらすべて調べよう。
(3)ラス問にしては取りやすいレベルであった。


コメント