平均49点(前年比;-5点)

問題PDF
大問1(小問集合)
(1) 93%
9-6÷3
=9-2
=7
(2) 75%
4x+2y=6
2y=-4x+6
y=-2x+3
(3) 85%
√27+√3-√12
=3√3+√3-2√3
=2√3
(4) 74%
x=2のとき、y=8
x=5のとき、y=50
変化の割合…(yの増加量)/(xの増加量)
(50-8)/(5-2)
=42/3=14
@別解@
y=ax2において、xの値がp→qと変化するときの変化の割合はa(p+q)
2×(2+5)=14
(5) 82%
偶数→一の位が2か4
十の位は何でも良い。
5枚のカードから2枚を選ぶので、確率は2/5
(6) 36%
弧の長さは直径から求めるから直径を文字に置き換える。
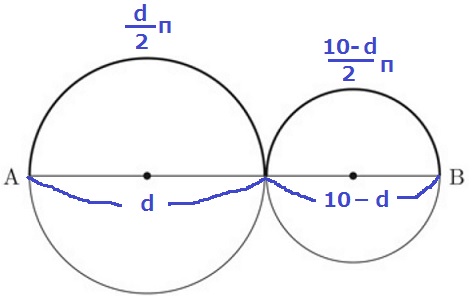
A側の円の直径をdとすると、B側の円の直径は10-d。
弧の長さの和は、d×π÷2+(10-d)×π÷2
=dπ/2+(10-d)π/2=dπ/2+5π-dπ/2=5πcm
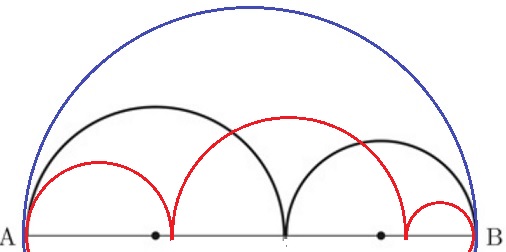
線分ABをどう分けようと、弧の合計は直径10cmの半円である。
大問2(データの活用)
(1) 52%
最頻値(モード)は最もあらわれている値。
20~25分の階級が最も人数が多い。
解答は階級値で求める。
20と25の平均である22.5。
(2) 66%
B中学校の15分未満の度数の合計は30。
30÷100=0.3
(3) 51%
ア:最頻値はAが22.5、Bが17.5。×
イ:39人の中央値は(39+1)÷2=20番目。Aの中央値は17.5。
100人の中央値は50番目と51番目の平均。Bの中央値は17.5で同じ。〇
ウ:A…13÷39=0.33… B…30÷100=0.3でAの方が大きい。×
エ:範囲(レンジ)=最大値-最小値。
度数分布表では階級の幅から最大値と最小値が確定できない。
しかし、全体でみるとAは5分以上35未満、Bは0以上40未満でBの範囲が広い。〇
イ・エ
@@

親子中学数学より。
度数分布表の範囲については複数の説がある模様。
テストでは本問のような明らかな形で出題されるので、とくに覚える必要はない。
大問3(整数)
(1) ア…53%、イ…56%、ウ…34%
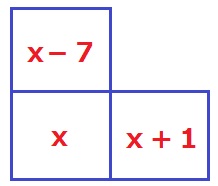
上下では下、左右では右の方が数値が大きい。
3マスの大小から位置関係を即答したい。
(ア)x-7
(イ)x+1
③より、
(x-7)2+x2=(x+1)2
x2-14x+49+x2=x2+2x+1
x2-16x+48=0
(ウ)x2-16x+48=0
(2) 34%
前問の式を解く。
x2-16x+48
=(x-4)(x-12)=0
2番目に小さい数をxとしている点に注目!
2番目に小さい数は最も小さい数の下にあるので2週目以降。
すなわち、xは1週目の1~7ではない。
x=12
2番目の数は12。
3つの数は5、12、13。
大問4(数量変化)
(1) ア…79%、イ…25%!
A側は高さ30cmまでは比例で上昇。
30×6/10=18cm
ア…18
30cmを超えると、A側の水がB側にはいる。
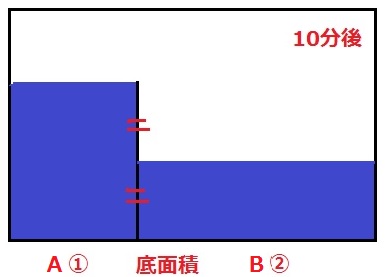
10分後の様子。
管aとbの給水速度は等しいので、AとBの水の体積は等しい。
奥行きは同じだから、うえの立面図でいえばAとBの長方形の面積が等しい。
底面積はA:B=1:2
高さは逆比でA:B=2:1
B側の水面の高さはしきりの半分。

★の面積が等しい。
管が1つだけだと10分かかるが、10分後からは管2つで★を埋めるので、
時間は半分の5分。
すなわち、15分後にA・Bの水面の高さは30cmとなる。
イ…30
(2) 31%!
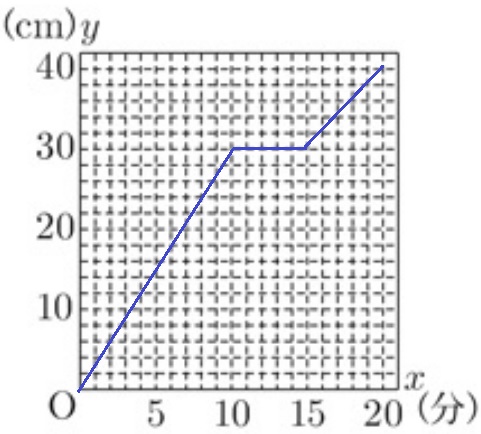
10分でしきりの30cmまで上昇。
5分間はB側に水がはいり変わらず。20分後に満水の40cm。
(3) ア…70%、イ…22%!
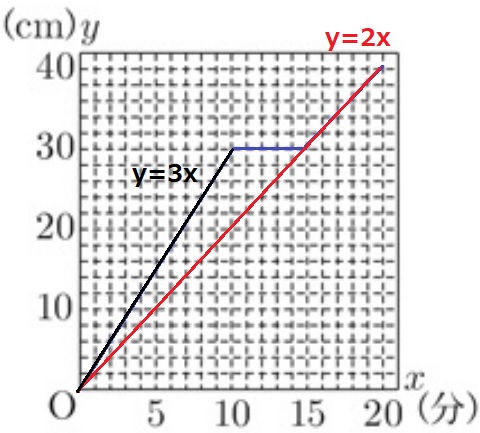
前問のグラフを利用する。
(ア)3x(イ)2x
(4) 12%!
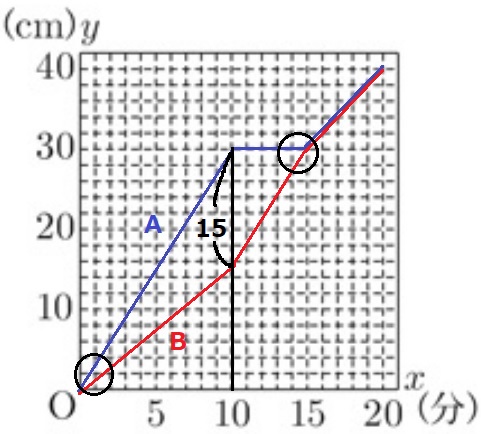
グラフにBを書き込んでみると、最初と15分前が怪しい。
10分後にAとBの差が15cmになる。
差が比例で広がっていくことに注目して、
10分×2/15=4/3分=1分20秒
10分後~15分後の5分間で差の15cmが0になる。
15分から時間を巻き戻すと、5分で15cmの差が生まれる。
2cmの差が生まれる時間は、5分×2/15=2/3分=40秒
15分-40秒=14分20秒後
1分20秒後、14分20秒後
大問5(平面図形)
(1) 59%
△ADB≡△AECの証明。

2つの直角二等辺三角形から2辺が等しいので、あいだの角に集中する。
90°から∠BAEをひくと★の角度が等しい。
2辺とあいだの角相等で合同。
(2)ア 69%
直角二等辺三角形ADEの辺の比は1:1:√2。
DE=3√2cm
(イ) 4%!!
BDという中途半端なところを求める。
しかし、BDを1辺とする直角三角形が見つからない…。
角度の調査を行う。
△ABCは直角二等辺。
AからDCに垂線をおろし、交点をFとする。
△ABFも直角二等辺で、1:1:√2からAF=BF=1cm

BD=xとして、△ABFで三平方。
(x+1)2+12=33
x2+2x-7=0
解の公式を適用。
x>0より、x=-1+2√2
BD=ー1+2√2cm
前問の誘導なしで解けた。
@@
YAさんから素晴らしい解法を頂きました。
△ABFの三平方でDF=2√2といったん出したうえで、
DB=DF-BF=2√2-1cmとした方が短時間で処理できます。
@別解@
公式解説にあった円周角の定理の逆はこういうことだと思う。
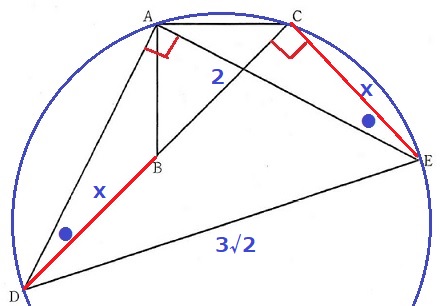
合同から∠ADC=∠AEC(●)
『2点D、Eが直線ACについて同じ側にあるとき、
∠ADC=∠AECだから、4点A、D、E、Cは同一円周上にある』。
円周角定理で、∠DAE=∠DCE=90°が導ける。
前問の合同からBD=CE=xとして、△CDEで三平方。
x2+(x+2)2=(3√2)2
これを解いて、x=-1+2√2
@@

円周角の定理の逆を使わなくても、∠ABC=45°から∠ABD=135°
合同で∠ACE=135°で、∠DCE=135-45=90°が導ける。
大問6(規則)
(1)(ア) 28%!

黒の碁石の縦の個数を見ると、
1→3→5…
4回目の黒の縦は7個。
これが2列できるので14個。
(イ) 27%!
正方形の1辺の個数は〔黒の縦の個数+2〕
4回目の正方形の1辺は7+2=9個
これが横に2行できるので18個。
(2) 52%
正方形の1辺の個数は、
3→5→7…
したがって、n回目は2n+1個。
*2n-1ではない!
奇数は2n-1だが、1回目の操作で3個なので最初の1は含まない。
n=1のときに値が3でなくてはならないので2n+1となる。
(3) ア…67%、イ…29%!、ウ…33%!、エ…19%!
着眼点が独特(;´Д`A
ア:問題文の図を観察。
1回目の操作で新たな黒は2個、新たな白は6個。
2回目の操作で新たな黒は6個、新たな白は10個。
新たにできる碁石の数は、常に黒より白が4個多い。
4個
イ:難所。
白の個数は(1+A+イ)個。
この1は始めに置かれた1個。Aが黒の数。それ以外がイとなる。

↑新たに並べられた黒と同数の白を赤枠で囲ってみた。
左上のはじめの1個を除くと、青枠の4個が黒より多い白の個数。
Aの形は複雑だが黒のAと相殺して無視すると、4個のグループが増えていく。
黒より多い白の個数4個は、n回目の操作でnグループ作られるので4n個。
白の個数は合計で(1+A+4n)個となる。
4n
ウ:(2)で正方形1辺が2n+1個だから、全体の碁石の個数は(2n+1)2個
(2n+1)2
エ:式を解く。
A+(1+A+4n)=(2n+1)2
2A+4n+1=4n2+4n+1
A=2n2
(4) 14%!
白の個数は1+A+4n個。
前問よりA=2n2だから、これを代入した2n2+4n+1を求めればいい。
n=20を代入して、881個。
@余談@
全体が(2n+1)2個。
黒は縦の個数が1、3、5…と奇数で増えていくが、
奇数の和で捉えると、1、4、9…と平方数になる。
これが2列あるので、n回目の黒の個数は2n2個。
n回目の白の個数は、(2n+1)2-2n2=2n2+4n+1個
これが最も思いつきやすいルートかと。
●講評●
以下、公式解答を適宜参照。
大問1
(5)十の位は何でも良い。何でも良い要素は無視。一の位だけを考える。
(6)無解答が多かった。特殊な出し方だが基本は変わらない。
大問2
(1)誤答では20~25が多かった。階級値の概念を忘れずに!
(3)誤答はウが多かった。
大問3
(1)『条件の文章がやや難解であったため、条件を正しく読み取ることができていない解答や
、無解答が多かった』。最初でつまづくと点差が開く。要点をつかむのは読解力。
大問4
(1)『誤答には10分後から20分後まで、A側の水面の高さが一定の割合で高くなるものと考えて、
(1)イでは35としたもの、(2)では(10、20)と(20、40)を直線で結んだもの、
(3)イではy=x+20としたものが多かった』
水槽の問題は正面から見た図を作成すること!何分後にどこの空間が埋まるかを把握する。
(4)無解答が多かった。
大問5
(1)誤答は∠DABと∠EACがともに90-∠BAEになることを適切に表現できていない。
(2)イ無解答多し。
大問6
(1)誤答は、n回目の操作で碁石を並べ直すものと捉え、ア32個、イ49個が多かった。
(3)誤答は、n回目の操作で白が黒より(4n+1)個多くなることが求められなかった。



コメント
分かりやすく求めることが出来ました!!
大変良かったです!!
ありがとうございます(*’ω’*)
合格、応援しています!