2020年度　日本大学第三高校過去問【数学】大問６解説

問題ＰＤＦ
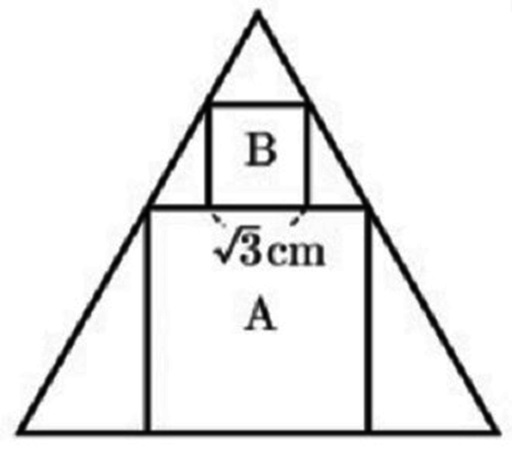
下の図のように、正三角形の中に正方形Ａと正方形Ｂが接している。
正方形Ｂの１辺の長さが√３ｃｍのとき、次の問いに答えなさい。

（１）
正方形Ａの１辺の長さを求めなさい。

（２）
正三角形の１辺の長さを求めなさい。

（３）
正三角形から正方形Ａと正方形Ｂを抜いた部分の面積を求めなさい。

＠解説＠
（１）

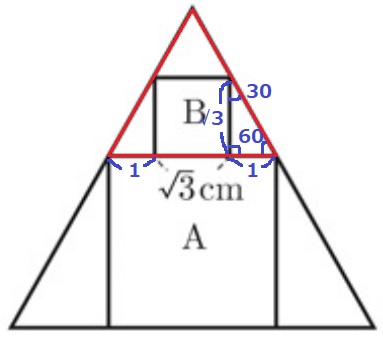
赤い三角形の底辺は正三角形の底辺と平行→正三角形

（２）

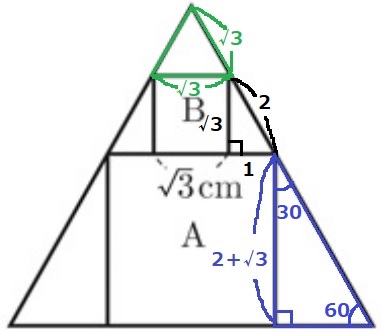
同様に、緑の三角形も正三角形で１辺は√３ｃｍ。
青い三角形は１：２：√３の直角三角形。
その斜辺は、（２＋√３）×２/√３＝２＋４√３/３ｃｍ
大きい正三角形の１辺は、√３＋２＋（２＋４√３/３）
＝４＋７√３/３ｃｍ

（３）
方針は立てやすい。
大きい正三角形から２つの正方形をひけばいい。

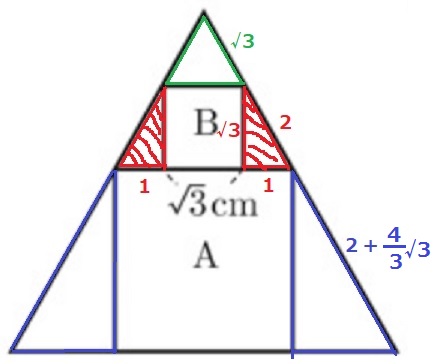
少し趣向を変えます。
左右の直角三角形を合わせると正三角形になる。
中段の正三角形（斜線の合計部分）の面積は、２×√３÷２＝√３ｃｍ²

３つの正三角形の面積比を斜辺の２乗から算出する。

面積比の【12】＝√３ｃｍ²なので、

49√３/12＋４ｃｍ²