2019年度　京都府公立高校入試問題過去問中期【数学】解説

問題ＰＤＦ

大問１（小問集合）

（１）
（－６）²－４²÷２
＝３６－８＝２８

（２）
（３ａ＋１）/４－（４ａ－７）/６
＝｛３（３ａ＋１）－２（４ａ－７）｝/１２
＝（ａ＋１７）/１２

（３）
√２７＋√２４×√８
＝３√３＋２√６×２√２
＝３√３＋４√１２
＝３√３＋８√３＝１１√３

（４）
代入法を使う。
９（２＋ｙ）－５ｙ＝２
４ｙ＝－１６
ｙ＝－４
ｘ＝２＋（－４）＝－２
ｘ＝－２、ｙ＝－４

（５）
３ａ²－２４ａ＋４８
＝３（ａ²－８ａ＋１６）　←はじめに共通因数３でくくる！
＝３（ａ－４）²

（６）
傾きが－２/３で、（－６、２）を通過する一次方程式。
２＝－６×－２/３＋ｂ
ｂ＝－２
ｙ＝－２/３ｘ－２

（７）

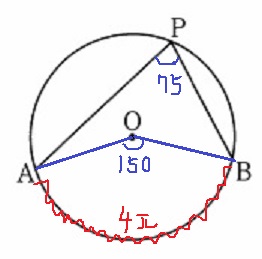
中心角150°で４πｃｍ。これが360°で円周。
４π×360/150＝４８/５πｃｍ

（８）
『少なくとも１枚は表』→全体－全て裏
全体…２³＝８通り
１－１/８＝７/８

大問２（データの活用）

（１）
２９個の中央値（メジアン）は、
（２９＋１）÷２＝１５番目のところ。
階級でいえば、〔６～１２〕分。
階級値は階級の真ん中の値→９分

（２）

資料が昇順にそろっているのがありがたい。
以上～未満に気を付けること！

（３）
正誤判定。
ア：18分未満は１組22人、2組21人。2組の方が少ない。×
イ：24以上は1組2人→2/29、2組2日→2/30。1組の方が割合が大きい。〇
ウ：１組6～18分→17人、2組12～24分→17人。等しい〇
エ：1組の0～6分は５人いるが、その中で３分未満がいるかもしれない。×
オ：問題はココ。
３年１組は個別の数値がわからないので、エと同様にわからないように思える。
試しに18分以上を数えると、１組が７人、２組が９人で計１６人。
ちょうど１６人いるので、大きい方から数えて16番目は2組の１８分の人。〇

大問３（空間図形）

（１）
球の表面積。Ｓ＝４πｒ²
Ｓ＝４π×（３/２）²＝９πｃｍ²
ＥＦの長さは次の問題の図参照。
５/３＋４＝１７/３ｃｍ

（２）
Ｘ…球の体積Ｖ＝４/３πｒ³
４/３π×（３/２）³＝９/２πｃｍ³

Ｙ…円柱と円錐を組みわせた図形になる。

円錐の高さは三平方で４。
2×2×π×5/3＋2×2×π×4×1/3
＝１２πｃｍ³
Ｘ：Ｙ＝９/２π：１２π＝３：８

大問４（方程式）

（１）
制動距離ｙ＝ａｘ²
0.5＝2²ａ
４ａ＝１/２
ａ＝１/８
ｙ＝１/８ｘ²

『ｙの増加量はｘの増加量の何倍か』→変化の割合を求めればいい。
ｘ＝５のとき、ｙ＝25/８
ｘ＝７のとき、ｙ＝49/８
（49/８－25/８）/７－５＝３/２倍

ｙ＝ａｘ²でｘの値がｐ→ｑに増加するとき、
変化の割合はａ（ｐ＋ｑ）であることから、
１/８×（５＋７）＝３/２…でもＯＫ！

（２）
秒速ｘｍとする。
1.5ｘ＋１/８ｘ²＝13.5
ｘ²＋12ｘ－108＝０
（ｘ＋18）（ｘ－６）＝０
ｘ＞0より、ｘ＝６　→秒速６ｍ

大問５（平面図形）

（１）

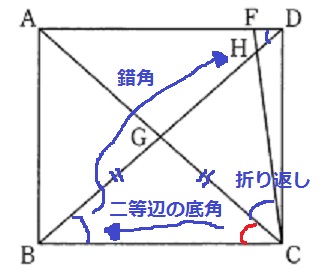
長方形の対角線は各々の中点で交わるので、二等辺の底角が等しい。
錯角でもう１つ。折り返しでもう１つ。
ア・オ・カ
（∠ＧＡＦも同じ大きさ）

（２）
長方形の縦横がわからず、直角が少なくて三平方が使えない(´ﾟдﾟ｀)
ＢＧをｘとする。

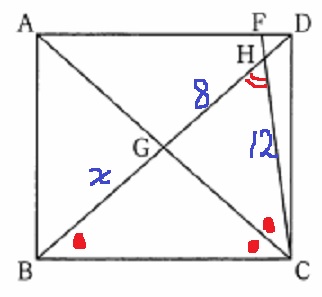
前問の角度をヒントにすると２角が等しく、△ＨＢＣ∽△ＨＧＣ
ＨＢ：ＨＣ＝ＨＣ：ＨＧ
ｘ＋８：１２＝１２：８
８（ｘ＋８）＝１２²
８ｘ＝８０
ｘ＝１０　　ＢＧ＝１０ｃｍ

（３）
当たり前だが、前問の攻略が前提条件。
△ＨＧＣの３辺は８：１０：１２。
△ＨＣＢより、ＢＣ＝10×18/12＝１５

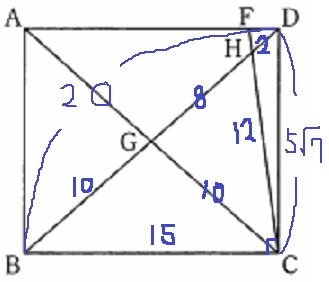
△ＤＢＣで三平方。ＤＣ＝５√７

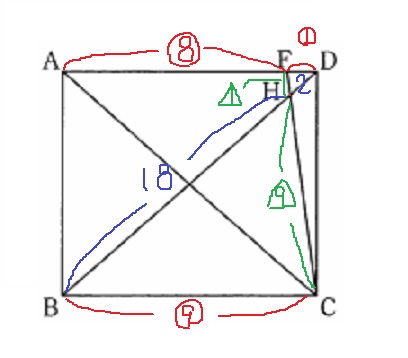
長方形→△ＡＣＤ（半分）→△ＦＣＤ→△ＤＦＨ
１５×５√７×１/２×１/９×１/１０＝５√７/１２cm²

大問６（規則）

（１）
例題のｍ＝３をまねて、ｍ＝４をやってみる。

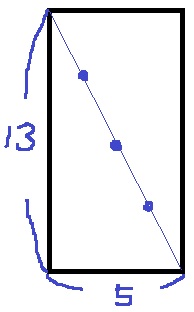
横は４＋１＝５
縦は４×３＋１＝１３
全体…５×１３＝６５個

周りの白は、
（１３＋５）×２－４＝３２
*各辺の足すと四隅が重複するので－４をしている。
中の白は、右に１、下に４。３つある。
白…３２＋３＝３５個
黒…全体－白＝６５－３５＝３０個

（２）
文字を使って、規則を一般化する。

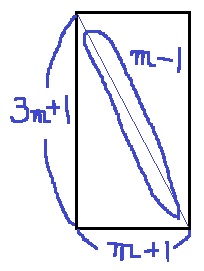
全体…（３ｍ＋１）（ｍ＋１）
周りの白…（３ｍ＋１＋ｍ＋１）×２－４＝８ｍ
中の白…ｍ－１
白の合計…８ｍ＋ｍ－１＝９ｍ－１
したがって、９ｍ－１＝４５８
ｍ＝５１

全体…（３×５１＋１）（５１＋１）＝８００８
黒…８００８－４５８＝７５５０
黒の個数を一般化すると、全体－白＝３ｍ²－５ｘ＋２個となります。
公立高校入試解説ページに戻る