平均64.2点
問題はこちら→リセマムさん
大問1(計算)-84.9%
(1) 97.8%
11+(-8)
=11-8
=3
(2) 94.4%
22÷(-2/5)
=4×(-5/2)
=-10
(3) 93.8%
2(3x+y)-3(x-2y)
=6x+2y-3x+6y
=3x+8y
(4) 78.1%
(3x-1)/2=(5x+2)/3
3(3x-1)=2(5x+2) ←両辺を6倍して分母をはらう
9x-3=10x+4 ←移項&左右反転
x=-7
(5) 73.9%
(√7-√5)(√7+2√5)
=7+2√35-√35-10 ←丁寧に計算。平方根の展開はミスが多発しやすい
=-3+√35
(6) 71.5%
(x-1)2-3(x-1)+2
=X2-3X+2 ←(x-1)をXに置き換えると因数分解可。
=(X-2)(X-1)
={(x-1)-2}{(x-1)-1}
=(x-3)(x-2) ←数学が得意な人は、頭の中で暗算してもOK。
大問2(小問集合)-65.5%
(1) 84.4%
連立でもいけるが、文字1つで等式ができるので一次方程式を利用。
52円の品物を買った個数をxとする。
82円の品物は(15-x)個買ったことになる。
52x+82(15-x)=1020
-30x=-210
x=7
ウ
(2) 74.5%
反比例の比例定数aは積xyなので、
a=2×(-6)=-12
y=-12/x
(3) 76.3%
@攻略1@
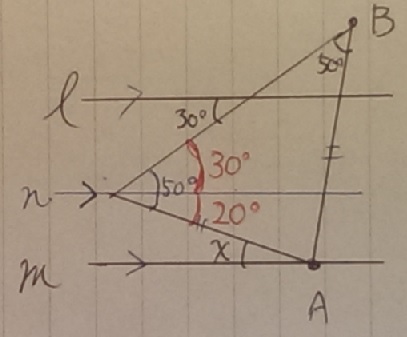
(C書くの忘れてしまった・・)
点Cを通り、直線ℓ、mに平行な直線をひく。
⊿ABCは二等辺三角形なので。∠ACB=50°
2段階錯角でx=20°
@攻略2@

上の三角形から攻めて、同位角を利用する。
∠BAC=180-(50+50)=80°
∠x=100-80=20°
(4) 43.6%
30の約数は、【1、2、3、5、6、10、15、30】
大小と2つのサイコロに区別がつくので、反対の組み合わせもカウントする。
1→(1,1)、2→(1,2)×2、3→(1,3)×2、5→(1,5)×2
6→(1,6)×2(2,3)×2 、10→(2,5)×2、15→(3,5)×2、30→(5,6)×2
起こりうるパターンは17通り
出目は全ては6×6=36通り
17/36
(5)6点―48.7% 3点―10.0% 無答―18.8%
前期と比べると、だいぶ大人しくなった。
後期は40分しか試験時間がなく、6点もあるのでこれくらいがちょうどいいかも。
サクサク処理して次の問題にいきたいところ。
大問1&2で60点分も稼げるので、満点を目指したい。
【1】問題文の手順でMを作成。(∠Cの二等分線)
【2】折るとMとDがくっつく=MDの垂直二等分線
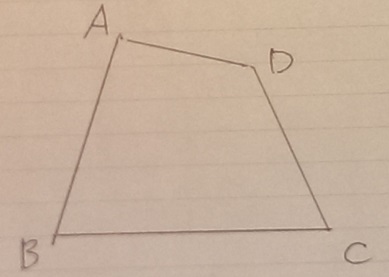
初期状態。
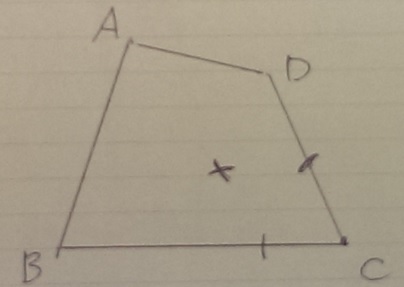
ピピ、ひょこひょこ。
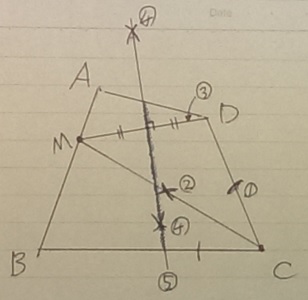
ここまでで各6点なので、ケアレスには注意したい。
大問3(関数)-37.6%
(1) 70.0%
AとBのx座標がともに判明している。

A(-2、8)B(1、2)
あとは直線ℓの式を求めるだけ。
連立でも良いが、グラフの傾きから求めてみよう。
A→Bは、右に3、下に-6
傾きは-6/3=-2
y=-2x+b
x=1、y=2を代入。
2=-2+b
b=4
y=-2+4
(2)6点―5.9%! 3点―9.5% 無答―58.4%!
時間がないので、少し考えてダメそうなら後回しでOK。

EとFのy座標は負なので、正方形は下にくる。
△ABOの面積は求められるが、
△ABPはその3倍となり、点Pは正方形の周上にある。
まず、△ABOの3倍の面積をもつ三角形を考える。
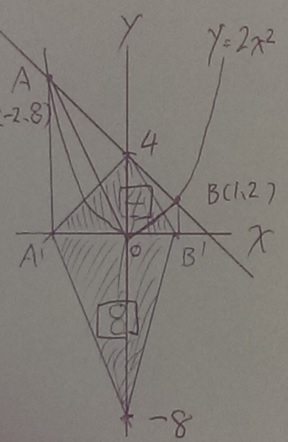
等積変形。AとBを平行移動させてx軸に下ろす。
青い斜線が面積3倍ゾーン。底辺A’B’で、高さの合計は12となる。
勘のイイ人は辺ABを底辺に、y軸に注目して3倍すれば(0、-8)が見つかるはず。

縦長になる。(0、-8)をGとする。
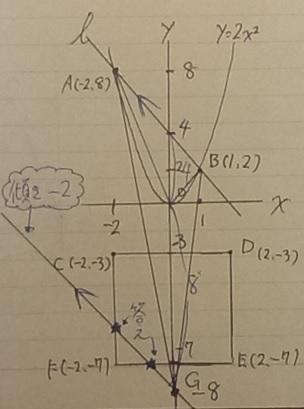
ここからGを通る、直線ℓと平行な直線をひく。
理由は、等積変形で△ABGと同じ面積になるから。
Gが正方形の周上にくるように平行移動させる。
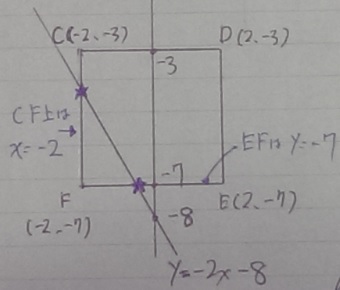
拡大。
平行線は、傾き-2、切片8だから、y=-2x-8
CF上はx=-2なので、上の式に代入。
y=-4
EF上はy=-7で代入。
x=-1/2
P(-2,-4)(-1/2,-7)
大問4(平面図形)-56.7%
(1)
等脚台形を用いた証明問題。
△PAQ∽△BCQの前に、△PAQ≡△DAQの証明。
(1)は前期よりも記述しやすいので、完答を目指したい。
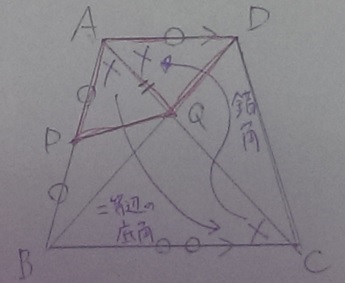
(見づらくて申し訳ない・・紫カメラ現象)
⊿PAQと⊿DAQに注目。等しい線に○、等しい角度に×を書いてみた。
PA=DA、AQは共通辺。
角度は、⊿BACから二等辺三角形の底角→錯角のコンボ。
よって、二辺と間の角が等しくなるので合同。
(a)イ (b)カ (c)ク 84.1%・84.4%・86.2%
(d)6点―25.9%! 3点―7.5% 無答―45.1%

辺の情報が乏しいので角度から攻める。
合同なので対応する角度が等しい。(●×■とおいた)
●と×は錯角、■は対頂角で等しくなる。
3つのうち2つを選んで、2角が等しい ことをいえばOK。
~引用はじめ~
(d) △PAQと△BCQにおいて、
∠AQD=∠CQB(対頂角) ・・・【7】
【6】より∠AQP=∠AQD ・・・【8】
【7】【8】より∠AQP=∠CQB ・・・【9】
【2】【9】より2組の角がそれぞれ等しいので、
△PAQ∽△BCQ
~引用おわり~
(2) 3.1%!
いろんな方向から図形を観察。
高さが等しい三角形は、底辺の比が面積の比となる。
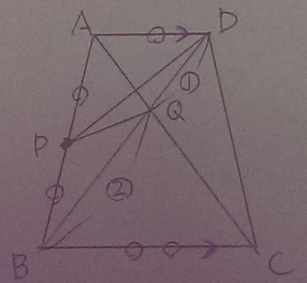
△ADQと△CBQは2角が等しく相似。
AD=○、BC=○○なので、相似比は1:2
DQ:QB=1:2
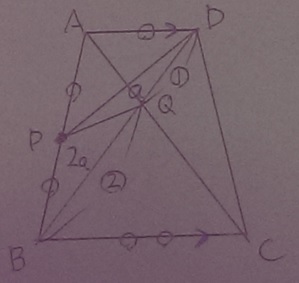
底辺の比から、△PQD:△PBQ=1:2
aで表すと、上のような感じ。

矢印の方向から眺める。
AP:PB=1:1
ゆえに△APD=3a

△BDA:△DBC=1:2(上底:下底=1:2だから)
△DBC=12a
等積変形で△DBC=△ABC=12
*等しい辺や角度に記号をつける。
視覚的にわかりやすい図形をつくれば突破口が見出せる。
いろんな方向から観察してみよう。
大問5(規則)-8.0%
(1)
今年の後期もラストに規則がきた。ただ、来年も同じ傾向がくるとは限らないので、
2011年大問3や2012年大問3、2013年(前)大問4、(後)大問3のような文章題にも慣れておきましょう。
【1】 17.1%!
PとQは半円(6cm)を往復する。
速さはP:1cm/s、Q:2cm/s
数量変化の鉄則は、転換点を見極めること!
ここでいう転換点は、P・QがAかBに到達したとき。
このとき、弧PQの長さycmが変化するので、グラフが折れる。
Pの変化は6、12秒後。Qは3、6、9、12、15秒後に変化。
xが3の倍数のときのyの値を地道に求めて、グラフにプロットする。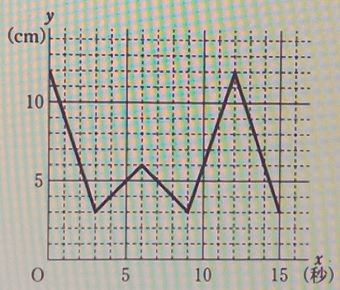
3秒後にQがAに到着したら、Pはどこにいるのか。
6秒後はどうか・・と15秒後まで頑張る。
【2】 6.9%!!
グラフをみると12秒ごとに同じ形が繰り返されることがわかる。
(後の会話にも同じことが書かれている)
円周12cmなので、弧PQが6cmになればPとQは正反対の位置にあり、
線分PQは直径となる。
0≦x≦12までにy=6の横線をグラフにひくと、
x=3、6、10秒後の3回、線分PQが直径となる。
つまり、1周期(12秒間)のなかで3回直径があらわる。
5分=300秒なので、300÷12=15周期
15周期×3回=75回
(2)【1】 10.4%!
前期と同様、文中にヒントが隠されている。
(1)をふり返り、どうやってグラフなしで1周期=12秒間を求められるかを考える。
PQは半円6cmを往復し、速さはP:1cm/s、Q:2cm/sであった。
PがBに戻ってくるのは12秒ごと、QがBに戻ってくるのは6秒ごと。
2つの点が再びBに戻るのは、12と6の最小公倍数で12秒後。
Bに戻ってくる時間の最小公倍数ですね。
(2)は、半円180cmを往復、速さはP:12cm/s、Q:15cm/s
PがBに戻るのは360÷12=30秒後、QがBに戻るのは360÷15=24秒後
24と30の最小公倍数である120が答え。
120秒
【2】 2.4%!!
落ち着いて対処すれば乗り越えられなくはない。
点Aを含む弧PQに対する円周角が18°とは、どんなときか?
円周角の定理を想起する。
円周角の定理によると、弧の長さが同じであれば円周角は同じ。
弧の長さが2倍になれば円周角も2倍。半分になれば半分・・。
→弧の長さと円周角の大きさは比例する。
円周角の2倍が中心角なので、弧の長さと中心角の大きさも比例。
下の図では、中心角を中心に書いてみた。
円周が360cm、1周が360°なので、cmを角度に変換。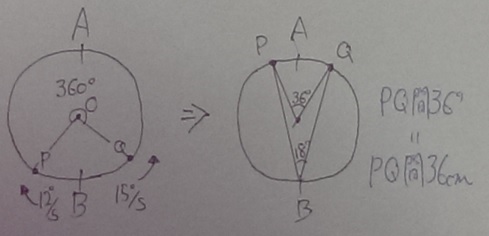
Pは毎秒12°で時計回り、Qは毎秒15°で反時計回りにBから回ることになる。
円周角18°=中心角36°(問題文に引き直せばPQ間は36cm)
あとは(1)【1】の通り、変換点に注意しながらリサーチ。
Qが先にAにつくので、180÷15=12秒後のPの位置を調べる。
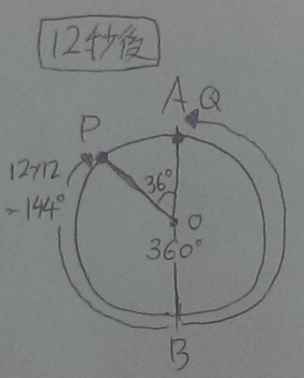
おや(゜Д゜)??
PQ間が36°・・よって、12秒後が答え。
@@
360cmといい、数字がありがたい。
仮にQがAを折り返す12秒以内に弧PQに対する中心角が36°となる瞬間があると確信できたら、
PとQで360-36=324°進めば良いことになる。
Pは毎秒12°、Qは毎秒15°進むから、
324÷(12+15)=324÷27=12秒後
x=12
【3】 3.0%!!
1210秒後の様子を考えろということだが、
【1】の通り、120秒周期でPQがともにBに戻ってくる。
120の倍数である1200秒後は、0秒後と同じ状態にリセットされる。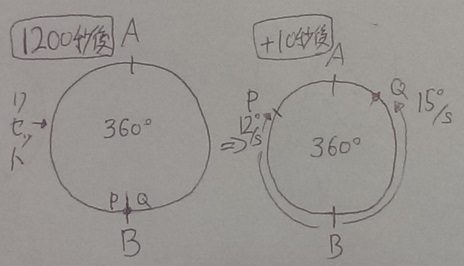
10秒後の様子を考えれば良いことになる。
12秒未満だから、まだQはAに到達していない。
Pは毎秒12°、Qは毎秒15°近づいていくので、
360-(12+15)×10=360-270=90°
PとQは90cm離れている。
y=90



コメント