平均30.3点（前年比；－0.2点）
問題はコチラ→ＰＤＦファイル
大問１（計算）
（１）
－８＋３
＝－５
（２）
９÷（－３/２）
＝－６
（３）
３＋６÷２
＝３＋３
＝６
（４）
√３×２√６ ←√６＝√３×√２に分解、√３×√３＝３
＝３×２√２
＝６√２
（５）
（－２ａ）2×５ａ3
＝４ａ2×５ａ3
＝20ａ5
（６）
５（２ｘ－ｙ）－２（３ｘ－ｙ）
＝10ｘ－５ｙ－６ｘ＋２ｙ
＝４ｘ－３ｙ
大問２（小問集合）
（１）
５ｘ＋３＝４ｘ－６
ｘ＝－９
（２）
ｘ＋３ｙ＝－５ …①
２ｘ－ｙ＝４ …②
①×２－②をすると、７ｙ＝－14
ｙ＝－２
②に代入、２ｘ－（－２）＝４
ｘ＝１
ｘ＝１、ｙ＝－２
（３）
（ｘ－３ｙ）2
＝ｘ2－６ｘｙ＋９ｙ2
（４）
ｘ2－25
＝（ｘ＋５）（ｘ－５）
（５）
ｘ2－７ｘ＋１＝０
解の公式を適用して、ｘ＝（７±３√５）/２
（６）
有理化。
５/√２ ←分母分子を√２倍
＝５√２/２
（７）
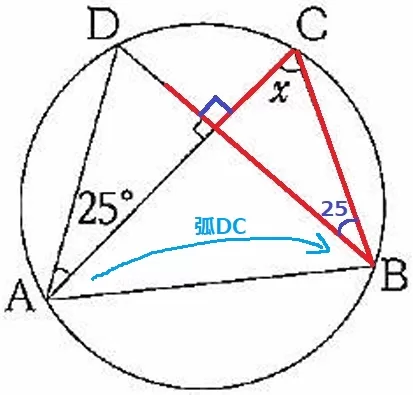
弧ＤＣの円周角で25°を移す。
赤線で外角定理→ｘ＝90－25＝65°
（８）
最頻値（モード）は最もあらわれている値。
度数（人数）が最も大きい23.5ｃｍ
（９）
２度目に捕獲したエビ28匹のうち、印付きは６匹だった。
全体：印付き＝28：６＝⑭：③
印付きは全部で30匹だから、エビの総数は30×⑭/③＝140匹
大問３（データの活用）
（１）
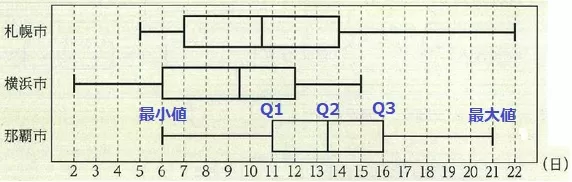
四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）
16－11＝５日
（２）
ア：最大値から降水量１ｍｍ以上の日が最も多い月は札幌市にあったが、
それぞれの日の降水量の具体的な数値は不明ゆえ、１年間に降った降水量はわからない。×
イ：いずれも中央値（Q2）は９日を超えるので、どの市も９日以上の月は半数（半年）以上。〇
ウ：Q2は６番目と７番目の平均で13.5日。第１四分位数（Q1）は下から３番目と４番目の平均で11日。
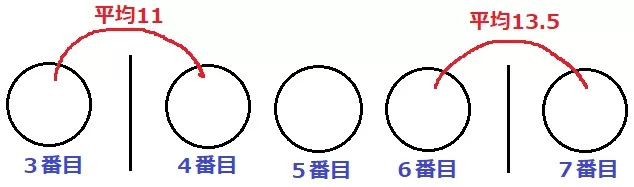
10日以上14日未満が最も少なくなるパターンを考える。
４番目は11以上、６番目は13以下。
４～６番目は10日以上14日未満だから３ヵ月以上ある。〇
エ：箱の長さ（四分位範囲）が最も短いのは那覇市。×
イ・ウ
（３）
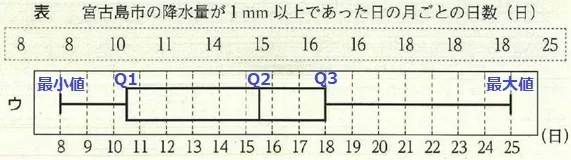
最小値…８日、最大値…25日
Q2…６番目と７番目の平均→15.5日
Q1…下位６個の真ん中、下から３番目と４番目の平均→10.5日
Q3…上位６個の真ん中、上から３番目と４番目の平均→18日
ウ
大問４（確率）
（１）
Ａの受け取り方は４通り、Ｂは残りの３通り、Ｃは残りの２通り、Ｄは残りの１通り。
４×３×２×１＝24通り
（２）
Ｂ・Ｃ・Ｄは考えなくていい。Ａだけを考える。
Ａのプレゼントはａ以外のｂ・ｃ・ｄ→確率は３/４
（３）
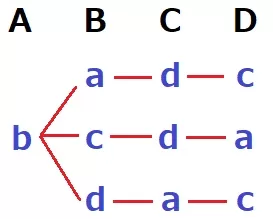
もし、Ａがｂを受け取った場合を樹形図で調べると３通り。
Ａがｃを受け取った場合も３通り。（ＡＣＢＤの順で調べると似た樹形図になる）
Ａがｄを受け取った場合も同様に３通り。（ＡＤＢＣの順で調べると似る）
計９通り、確率は９/24＝３/８
＠完全順列（攪乱順列）＠
プレゼント交換や席順の問題のように各要素が最初と同じ場所にならない順列を、
数学の世界では完全順列（攪乱順列）といいます。
早稲田中学で出題されました。
ｎ個の完全順列の総数はモンモール数（Ｄｎ）というそうで、
Ｄ0＝１、Ｄ1＝０、Ｄ2＝１、Ｄ3＝２、Ｄ4＝９、Ｄ5＝44
Ｄ6＝265、Ｄ7＝1854、Ｄ8＝14833…
（本問はＡ～Ｄの４人だからＤ4＝９通り）
高校数学で習う漸化式を使って、これらの数字の並びを一般化すると、
Ｄｎ＝（ｎ－１）（Ｄｎ－２＋Ｄｎ－１）
〔ｎ番目のモンモール数は、ｎ－１の値に２個前と１個前のモンモール数の和をかける〕
Ｄ3＝（３－１）×（１＋０）＝２
Ｄ6＝（６－１）×（９＋44）＝265
Ｄ8＝（８－１）×（265＋1854）＝14833、と計算でモンモール数を導けます。
高校数学の美しい物語より。
このページによりますと、完全順列の総数を十分に大きくすると、
元の場所と位置が完全に変わっている確率は37％程度に落ち着くようです。
自分のプレゼントが当たる人が少なくとも１人でてくる確率は約63％。意外と大きな数値で驚きです。
大問５（数量変化）
（１）
製本料金は100冊、印刷料金は50冊分でカウントする。
10000+50×100+30×50
＝16500円
（２）
枚数で変わらない固定費は、基本料金の5000円→切片＋5000
枚数で変わる変動費は、製本料金と印刷料金を合わせて１枚あたり80円→傾き80
ｙ＝80ｘ＋5000
（３）
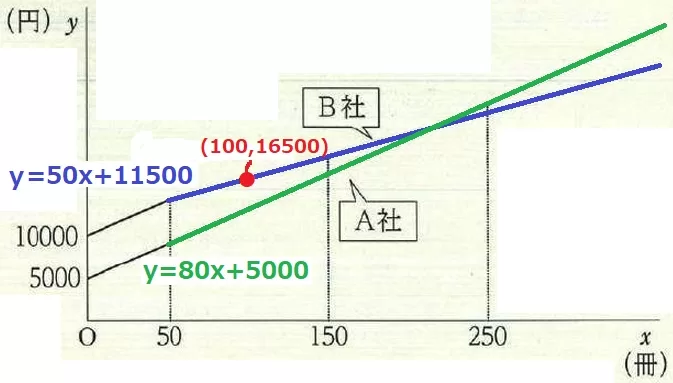
Ｂ社は50冊以降、傾き50で変わらない。
（１）より（100、16500）を通るから、左に100、下に100×50＝5000移動して、
切片は16500－5000＝11500
Ｂ社；ｙ＝50ｘ＋11500（ｘ≧50）
Ａ社との交点座標は、50ｘ＋11500＝80ｘ＋5000
30ｘ＝6500
ｘ＝216.6…
216冊まではＡ社が安く、217冊からＢ社が安くなる。
217冊以上
大問６（整数）
（１）
図１は５列だったが、図３は６列に変わる。
13×15－８×20＝35
（２）
流れは例題を真似すればいい。
上の数をｎとすると、左はｎ＋５、右はｎ＋７、下はｎ＋12。
（ｎ＋５）（ｎ＋７）－ｎ（ｎ＋12）
＝ｎ2＋12ｎ＋35－ｎ2－12ｎ＝35
したがって、左右の積から上下の積をひいた値はいつも35である。
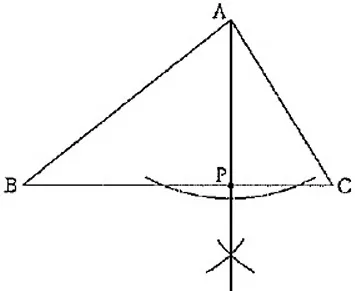
大問７（作図）
Ａを通るＢＣの垂線をひき、ＢＣとの交点がＰ。
大問８（関数）
（１）
ｙ＝ａｘ2に（２、２）を代入。
２＝４ａ
ａ＝１/２
（２）
ｙ＝ａｘ2において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
１/２×（－２＋４）＝１
（３）
ｙ＝１/２ｘ2に－２、４を代入。
C（－２、２）→Ｂ（４、８）
右に６、上に６だから、傾きは６/６＝１
Ｃから右に２、上に２移動して、切片は２＋２＝４
ｙ＝ｘ＋４
（４）
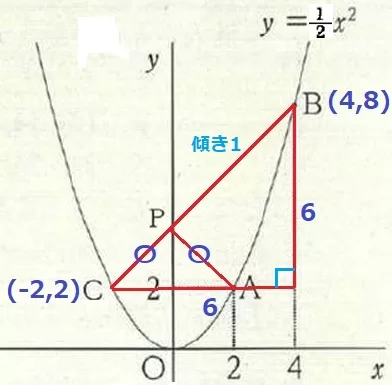
ＡＰ＋ＢＰが最も小さくなる。
→Ａをｙ軸について対称移動させたＣとＢを直線で結び、ＣＢとｙ軸との交点がＰになればいい。
（線対称でＡＰ＝ＣＰ→ＡＰ＋ＢＰ＝ＣＰ＋ＢＰ＝ＣＢ）
ＣＢを斜辺とする直角三角形をつくる。
ＣＢの傾きは１→辺の比は１：１：√２の直角二等辺三角形（等辺６）。
ＣＢ＝ＡＰ＋ＢＰ＝６√２
大問９（平面図形）
（１）
∠ＱＰＲ＝180－30×２＝120°
（２）
△ＰＡＲ≡△ＰＱＢの証明。
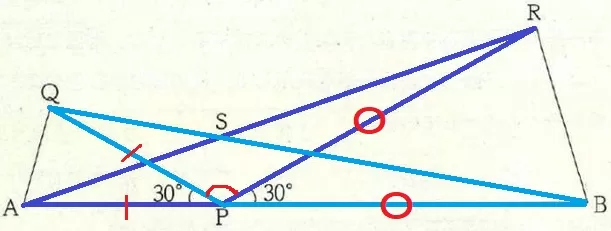
二等辺の等辺から、ＰＡ＝ＰＱ、ＰＲ＝ＰＢ
∠ＡＰＲ＝∠ＡＰＱ＋∠ＱＰＲ
∠ＱＰＢ＝∠ＢＰＲ＋∠ＱＰＲ
∠ＡＰＱ＝∠ＢＰＲだから、∠ＡＰＲ＝∠ＱＰＢ
２辺とあいだの角が等しいので合同。
（３）
角度の情報が乏しい。
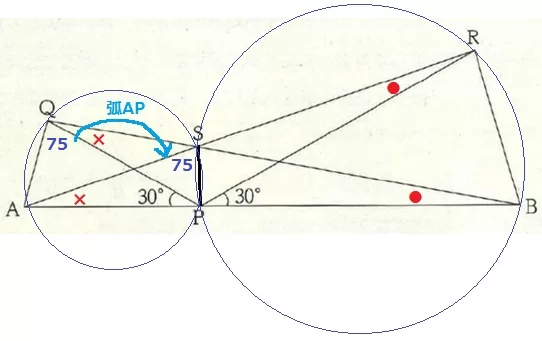
選択肢の前半は同一円周上にある４点に言及するので、円周角の定理の逆を疑う。
ＳＰに補助線。前問の△ＰＡＲ≡△ＰＱＢの対応する角に印をつける。
ＢとＲはＳＰについて同じ側にあり、∠ＰＢＳ＝∠ＰＲＳ（●）だから、
円周角の定理の逆から４点Ｐ・Ｂ・Ｒ・Ｓは同一円周上にある。（ア）
同様に、∠ＰＡＳ＝∠ＰＱＳ（×）から４点Ｐ・Ａ・Ｑ・Ｓも同一円周上にある。
△ＡＰＱは二等辺→∠ＡＱＰ＝（180－30）÷２＝75°
弧ＡＰの円周角で移して、∠ＡＳＰ＝75°（ウ）
ア・ウ
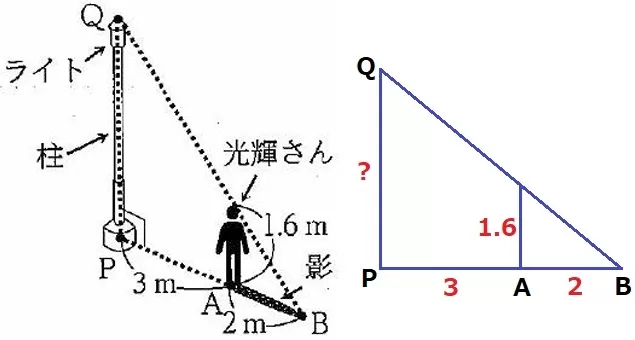
大問10（空間図形）
（１）
半径５ｍの円周を求める。
５×２×π＝10πｍ
（２）
ＰＱ＝1.6×５/２＝４ｍ
（３）
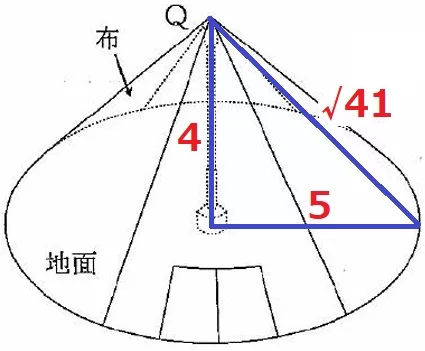
三平方の定理から母線は√41ｍ。
円錐を展開すると、布は半径√41ｍの扇形。中心角は〔×半径/母線〕で対処する。
√41×√41×π×５/√41＝５√41πｍ2
大問11（文章題）
（１）
最初の余りがビー玉。
２回目の商が小箱、余りが袋。
（２）
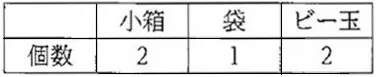
ｎ＝３で手順を逆にする。
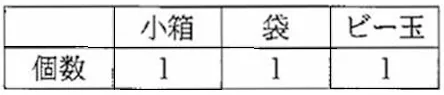
①【小箱＋袋⇒袋の総数】
②【袋の総数＋ビー玉⇒ビー玉の総数】
袋の総数は、３×２＋１＝７個
ビー玉の総数は、３×７＋２＝23個
（３）
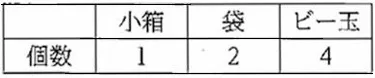
袋の数の総数は、ｎ×１＋２＝ｎ＋２個
ビー玉の数の総数は、ｎ（ｎ＋２）＋４＝52
ｎ2＋２ｎ－48
＝（ｎ－６）（ｎ＋８）＝０
ｎ＞０だから、ｎ＝６
ゆたぼん君が挑んだ問題です。
大問１
必答。
大問２
ここも全問正解を狙いたい。
（９）２回目に捕獲した28匹のうち、印付きは６匹。
この割合は母集団全体でも同じとみなす。
大問３
（２）ウ：10日も14日も四分位数ではないため、差がつきやすいか。
第１四分位数と中央値から範囲を絞る。
大問４
正答率は高くなさそう。樹形図で調べるのが確実だが、時間配分に気をつけよう。
（１）順列で考える。
（２）Ａだけを問われる→ＢＣＤは何でもいいので、Ａだけを考えればいい。
（３）ここは樹形図を使う必要はあるが、工夫すればｂだけでＯＫ。
大問５
（２）製本料金と印刷料金はまとめる。
（３）前問でＡ社の式を求めたので、Ｂ社を出して交点座標を調べる。
桁が大きいので計算ミスに注意！
大問６
（２）オーソドックスだが、結論部分まで素早く書く。
大問７・８
点を積み重ねたい。
大問９
（３）選択肢の構造から（ア・イ）（ウ・エ）から１つずつ選ぶ。
４点が同一円周にある→円周角の定理の逆→角度調査。前の合同を用いる。
大問10
取りやすい部類です。
（３）円錐の側面積は母線と半径で求まる。
大問11
操作を理解すれば取りやすい。
（２）小箱をばらして袋の総数。袋をばらしてビー玉の総数。
公立高校入試解説ページに戻る
コメント