平均54.6点
問題はコチラ→ＰＤＦファイル
2019年度大阪府Ａ問題・Ｃ問題は別ページ。
大問１（小問集合）
（１） 90.6％
４2－（－６）÷２
＝16－（－３）＝19
（２） 93.9％
２（５ａ－３ｂ）－７（ａ－２ｂ）
＝10ａ－６ｂ－７ａ＋14ｂ
＝３ａ＋８ｂ
（３） 90.8％
18ｘｙ3÷（－３ｙ）2
＝18ｘｙ3÷９ｙ2
＝２ｘｙ
（４） 81.2％
（√７＋２√５）（√７－２√５）
＝（√７）2－（２√５）2
＝７－20＝－13
（５） 47.1％
最頻値（モード）は度数が最も大きい階級の階級値。
100以上110未満の階級で、階級値はこの平均。
（100＋110）÷２＝115
（６） 80.4％
負＋負＝負なので、イ。
数直線で表せば、原点の左から左に進む。
アは負×負＝正で、常に正となる。
ウはカッコ内がイと同じで負なので、全体として正となる。
エも最後に２乗するから正。
（７） 62.2％
（ｘ＋４）（ｘ＋５）＝210
ｘ2＋９ｘ－190
＝（ｘ－10）（ｘ＋19）＝０
ｘ＞０より、ｘ＝10
（８） 49.0％
（Ａ、Ｂ）より（大、小）と考え、大の値に３の倍数をあてる。
（大、小）＝（３、２）（６、１）（６、３）（６、５）（９、２）（９、４）（９、６）
以上、７通り
全体は、３×５＝15通り
７/15
（９） 50.8％
説明記述。
ＡとＢの座標を求める→連立→ｙ＝ａｘ＋ｂの切片ｂが答え。
Ａ（２、４） Ｂ（－３、９/４）
４＝２ａ＋ｂ
９/４＝－３ａ＋ｂ
これを解いて、ａ＝７/20、ｂ＝33/10
ｙ＝７/20ｘ＋33/10
よって、33/10
大問２（数量変化）
（１）Ａ問題と同じ。
① ア…90.4％ イ…88.6％
最初が40、以降＋90が続く。
ア…310、イ…580
② 71.0％
式の一般化。
＋90は（ｘ－１）回であることに注意！
ｙ＝40＋90（ｘ－１）
ｙ＝90ｘ－50
③ 72.8％
前問の式で、ｙ＝1660を代入。
ｘ＝19
（２） 21.2％！
ＯＰ間は前問と同じなので、
ｙ＝90ｘ－50の式にｘ＝23を代入してＯＰ間を算出。
ｙ＝2020 …ＰＲ間
ＯＲ間からＯＰ間とＰＱ間を除外してＱＲ間を求める、
3490－2020－200＝1270
ＱＲ間は、ｙ＝40＋（ｘ－１）ａ
これに、ｘ＝16、ｙ＝1270を代入。
1270＝40＋15ａ
ａ＝82
大問３（平面図形）
（１） 63.1％
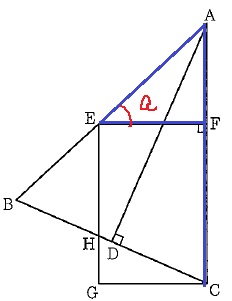
↑ここで外角定理。
∠ＥＡＦ＝90－ａ°
（２） 37.9％
△ＡＢＤ∽△ＣＨＧの証明。
辺の長さの情報が乏しいので角度で攻める。
△ＡＢＣは二等辺。
二等辺の底角→三角＋直角で２角が等しい。
（３）① 50.0％
前問の相似を利用する。
ＢＤ：ＢＡ＝ＨＧ：ＨＣ＝２：５
ＢＡ＝11だから、ＢＤ＝11×２/５＝22/５ｃｍ
② 0.4％!!!
ＦＣ＝ＥＧなので、ＥＨの長さが欲しい。
なんとなく△ＥＢＨが二等辺に見える…。
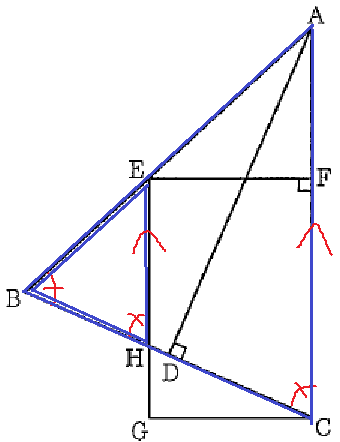
ＥＨ//ＦＣより、同位角で∠ＢＨＥ＝∠ＢＣＡ
２角が等しいので、△ＥＢＨ∽△ＡＢＣ
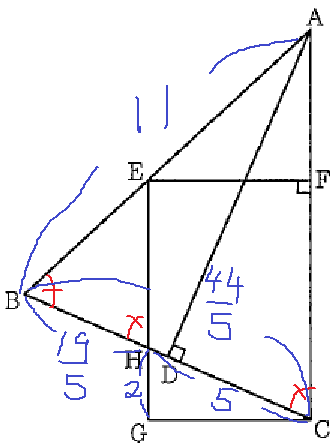
前問から、ＢＤ＝22/５なので、
ＢＣ＝ＢＤ×２＝44/５
ＢＨ＝44/５－５＝19/５
ＢＨ：ＢＣ＝19/５：44/５＝19：44
相似より、ＥＢ：ＡＢ＝19：44だから、
ＥＢ＝11×19/44＝19/４
△ＥＢＨは二等辺なので、ＥＨ＝19/４
ＦＣ＝ＥＧ＝19/４＋２＝27/４ｃｍ
大問４（空間図形）
（１）① 89.2％
ねじれの位置⇒交わらない＆平行でない
エ
② 79.3％
△ＥＧＨに着目。
ＧＨ＝４、ＥＦ＝４→△ＥＧＨは直角二等辺三角形。
ＥＧ＝４×√２/１＝４√２ｃｍ
③ 9.0％!!
四角形ＥＩＣＦは菱形。
菱形の面積＝対角線×対角線÷２
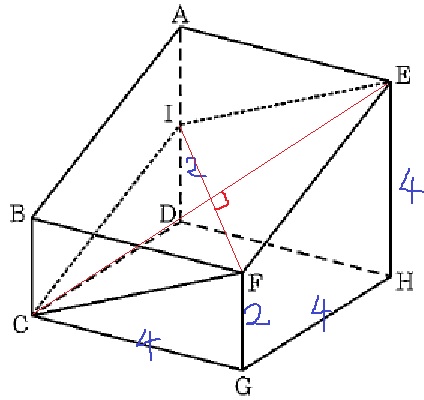
ＩＦは、底面である正方形ＤＣＧＨの対角線ＤＧと平行である。
１：１：√２から、ＩＦ＝４√２
ＣＥはＣＧ、ＧＨ、ＨＥを１辺とする直方体の対角線。
ＣＥ＝√（４2＋４2＋４2）＝√48＝４√３
したがって、４√２×４√３÷２＝８√６ｃｍ2
（２）① 8.1％!!
側面の台形ＦＧＨＥをピックアップ。
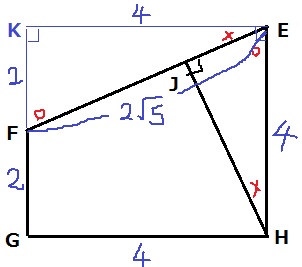
上のように長方形をつくり、左上の頂点をＫとする。
○＋×＝90を利用して角度を調べていくと、
２角が等しいことから、△ＥＪＨ∽△ＦＫＥ
△ＦＫＥで三平方→ＦＥ＝２√５
ＥＪ＝２×４/２√５＝４√５/５ｃｍ
② 0.4％!!!
△ＢＦＪは地面と平行ではないので、
△ＢＦＧか△ＦＧＪのどちらかを底面におけばいい。
以下、△ＢＦＧを底面とします。
高さはＬＪになる。
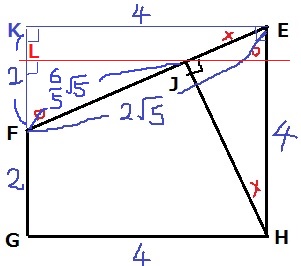
前問の図に追加すると、ＬＪはココ↑
△ＬＦＪ∽△ＫＦＥから、
ＬＪ＝４×（６√５/５）/ ２√５＝12/５
４×２÷２×12/５÷３＝16/５ｃｍ3
公立高校入試解説ページに戻る
コメント