平均33.9点（前年比；＋3.8点）
問題はコチラ→ＰＤＦファイル
出題範囲の除外は相似な図形、円周角の定理、三平方の定理、標本調査。
大問１（小問集合）
（１） 64.9％
ｘ2＋３ｘ－１＝０
解の公式を適用。
ｘ＝（－３±√13）/２
（２） 62.5％
３枚の硬貨の出方は２3＝８通り
60円未満の方が少ない。60円未満が表となるのは０円・10円・50円の３通り。
60円以上は８－３＝５通り
確率は５/８
ア…８、イ…５、ウ…５/８
（３） 69.3％
最頻値（モード）が含まれる階級は210～230ｃｍ。
相対度数は、20÷80＝0.25
（４） 55.5％
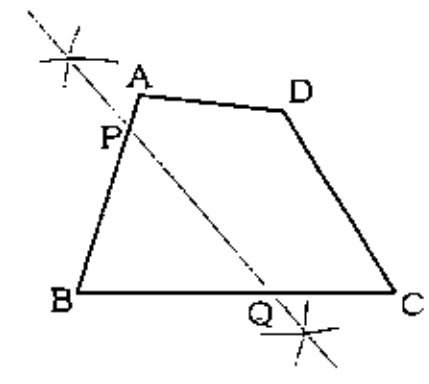
『ＢとＤが重なる』→ＢとＤが対応する点となるような対称の軸が折り目。
ＢＤの垂直二等分線を作図し、辺ＡＢ、ＢＣとの交点がＰ、Ｑとなる。
大問２（規則）
（１） 44.6％
五角形を２個つくる。５＋４＝９本
３個つくる。９＋４＝13本
五角形を１個増やすと、ストローは４本ずつ増える。
規則を一般化する。
はじめのストローは５本。
２個目以降は（五角形の個数－１）×４本が追加される。
５＋４（ｎ－１）
ア…９、イ…13、ウ…４、エ…ｎ－１
（２） 23.9％！
説明問題。
例題と同じように考える。
うえのように区切ると最初は11本で、８本の固まりがｎ－１個。
11＋８（ｎ－１）
＠別解＠
最初に３本おき、８本ずつ足していくこともできる。
この場合、８本はｎ個に相当するので８ｎ＋３と式がややスッキリする。
大問３（関数）
（１） 67.6％
ｘ軸について対称なので、上に凸のグラフに変わる（傾きは負）
ｙ＝－４ｘ2
（２） 64.4％
ｙの変域が０以上だから、下に凸のグラフ。
ｘ＝３のとき、最大値ｙ＝18
ｙ＝ａｘ2に（ｘ、ｙ）＝（３、18）を代入。
18＝９ａ
ａ＝２
（３） 15.0％！
説明問題。
よくある形式ゆえ解けるようにしておきたい。
ＡＣ＋ＢＣの最短距離。
Ａをｙ軸について対称移動させたＡ’とＢを直線でひく。
Ａ（－２、４）⇒Ｂ（３、９）
右に５、上に５だから傾きは１。
Ａ’から右に２、上に２移動して、切片は４＋２＝６
Ｃ（０、６）
大問４（平面図形）
（１） 73.1％
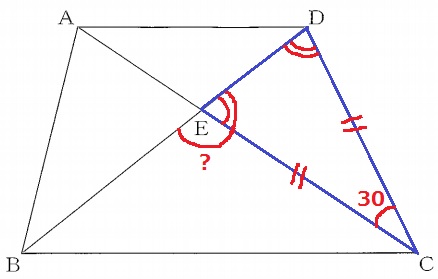
△ＣＤＥは二等辺三角形。
∠ＣＥＤ＝（180－30）÷２＝75°
∠ＢＥＣ＝180－75＝105°
（２） 25.2％！
ＡＤ＝ＨＢの証明。
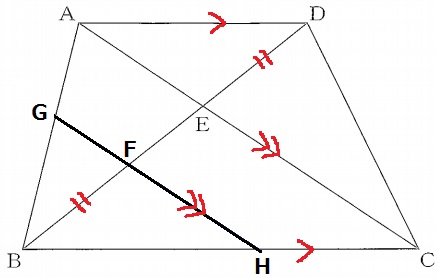
問題文にしたがって情報を加える。
ＡＤ＝ＨＢを証明したいので、これらを１辺とし、かつ情報の多そうな三角形に着目する。
→△ＡＤＥと△ＨＢＦの合同を指摘すればいい。
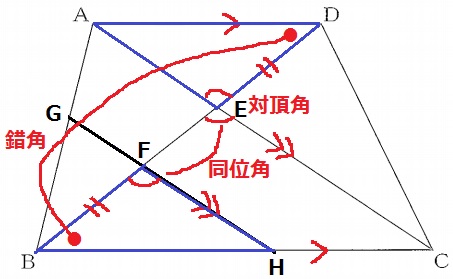
仮定より、ＤＥ＝ＢＦ
ＡＤ//ＢＣの錯角で、∠ＡＤＥ＝∠ＨＢＦ
対頂角とＡＣ//ＧＨの同位角で、∠ＡＥＤ＝∠ＨＦＢ
１辺と両端角が等しく、△ＡＤＥ≡△ＨＢＦ
対応する辺は等しいから、ＡＤ＝ＨＢ
大問５（学校裁量問題）
（１）① 26.3％！
最初と最後は思いつきやすいが、初見だとあいだの部分が迷いやすい。
扇形の弧（両端以外）が地面と接しているとき、中心点が通過する部分は直線になる。
地面は扇形の接線であり、接線と半径は常に垂直である。
接点（地面）から中心までの距離は常に半径の長さで一定となる。
Ｐが通過する長さは、半径２ｃｍ中心角90°の弧２つと、
直線部分である半径２ｃｍ中心角120°の弧ＱＲの合計。
２×２×π×１/２＋２×２×π×１/３
＝10/３πｃｍ
② 15.2％！
前問と同様に考える。
弧が地面と接しているとき、中心が通過する軌跡は直線になる。
本問の図形は、半径が等しい扇形の弧と地面が常に接するので直線になる。
ウ
＠ルーローの三角形＠
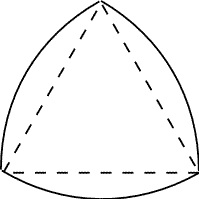
お掃除ロボットで採用されている有名な三角形。
数学のコラムではマンホールの話にもよく出てくる。
マンホールのフタが円形なのは、円の最大幅はどこも同じで、
どんな向きにしてもフタが落下せず、未然に事故を防ぐことができるため。
ルーローの三角形も最大幅が一定である。
コロコロ転がしてもテーブルと床は一定の距離で平行を保つ。
↑ルーローバイクを楽しんでいるおじさん。走りにくそう(;^ω^)
三角形がシンクロしてるのが良い。
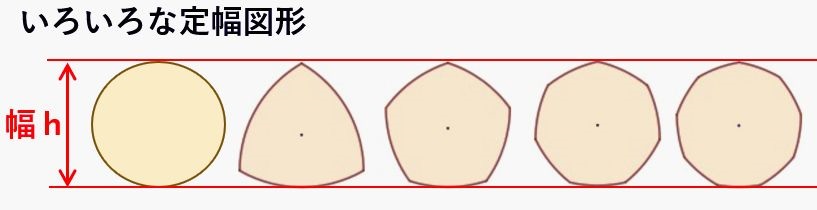
温故知新ラーニングより。
幅が一定である図形を定幅図形といい、
頂点の数が奇数であれば、三角形以外にも様々なルーローの多角形が存在する。
（２）① 51.2％
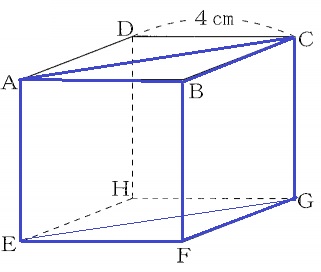
切断面は平行を意識する。
ＡＣに平行な線分はＥＧ。長方形ＡＥＧＣで切られる。
三角柱ＡＢＣ―ＥＦＧを求積すればいい。
４×４÷２×４＝32πｃｍ3
② 32.1％！
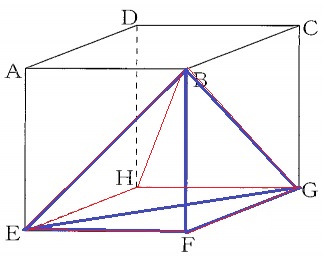
錘は柱の体積の３分の１。
四角錘Ｂ―ＥＦＧＨの体積は立方体の１/３倍。
三角錐Ｂ―ＥＦＧの底面△ＥＦＧは正方形ＥＦＧＨの半分だから、
三角錘Ｂ―ＥＦＧの体積は立方体の１/６倍。
③ 5.1％!!
説明問題。
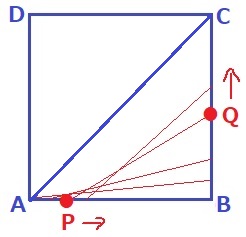
Ｐ：Ａ→Ｂ→Ｃ（毎秒１ｃｍ）
Ｑ：Ｂ→Ｃ→Ｄ→Ａ→Ｂ（毎秒２ｃｍ）
ＰとＱは正方形ＡＢＣＤの辺上を動く。
ＥＧとＡＣが平行だから、ＰＱがＡＣと平行になるときを考える。
ＡＣは斜め45度線。１回目はＱがＣに着く前にありそう。
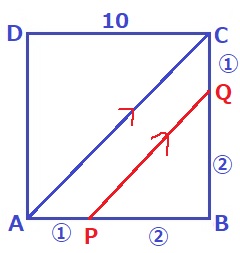
ＰとＱの速さの比は１：２。
ＡＰ＝①とすると、ＢＱ＝②
平行線から△ＡＢＣ∽△ＰＢＱ→ＡＰ：ＰＢ＝ＣＱ：ＱＢ＝①：②
ｘ（①）＝10×①/③＝10/３
＠＠
範囲から除外された相似を使ってしまいましたが、
ＰＢ＝10－ｘ、ＢＱ＝２ｘと長さを求め、
ＰＢ＝ＢＱより、10－ｘ＝２ｘ
ｘ＝10/３と方程式で解けます。
５秒ごとに調べてみると、15秒後までにＡＣとＰＱが平行になる瞬間はなさそう。
次にＡＣ//ＰＱとなるのは、ＰがＢＣ上、ＱがＡＢ上にあるとき。
ＰＢの長さ…（Ｐが動いた距離）－ＡＢ＝ｘ－10ｃｍ
ＱＢの長さ…（正方形ＡＢＣＤの周の長さ）－（Ｑが動いた距離）＝40－２ｘｃｍ
ＰＢ＝ＱＢ
ｘ－10＝40－２ｘ
ｘ＝50/３
したがって、10/３秒後、50/３秒後。
一応、学校裁量問題であるものの、コロナ禍を差し引いても全体的に易問である。
大問１
（２）誘導なしで普通に５/８を問えば良かったと思う。
（３）安直な相対度数の計算。
（４）教科書レベルの作図。
大問２
空欄補充は初学者用のワークか？
（２）下にもう１個正六角形をつけただけで、
難関校を受ける者にとっては何の腹の足しにもならない。
大問３
定番で平々凡々なレベルを何故３題も出した(´ﾟдﾟ｀)!?
大問４
（１）小学４年生でも解ける。
（２）きちんと図示する。等辺がわかっているので両端角に目をつける。難しくはない。
大問５
（１）高校受験ではあまり見かけないが、中学受験では基本に相当する。
演習を積み重ねてカバーしよう。
（２）体積は易！
③ＰＱの角度は０°から上昇し、45°となる１回目はＱがＣに着く前。
２回目はやや離れる。Ｑが頂点に到着する５秒おきを手早く調べる。
計算は複雑ではない。時間が余ったと思うので、確実に決めておきたい。
公立高校入試解説ページに戻る
コメント