2024年度　大阪府公立高校入試Ａ問題過去問【数学】解説

問題はコチラ→ＰＤＦファイル
2024大阪（数学）Ｂ問題の解説はコチラ。

大問１（計算）

（１）
６－（－１）×２
＝６－（－２）
＝６＋２
＝８

（２）
９÷（－３/４）
＝９×（－４/３）
＝－12

（３）
５²＋（－15）
＝25－15
＝10

（４）
ｘ－３＋４（ｘ＋１）
＝ｘ－３＋４ｘ＋４
＝５ｘ＋１

（５）
２ｘｙ×３ｘ
＝６ｘ²ｙ

（６）
６√２－√８
＝６√２－２√２
＝４√２

大問２（小問集合）

（１）
３ａ－５
＝３×６－５
＝13

（２）
整数→負の整数＋０＋正の整数
－4.8より大きく、2.2より小さい整数は、
－４、－３、－２、－１、０、１、２の７個。

（３）
ａとｂの和が５ｋｇより大きい。
ａ＋ｂ＞５
イ

（４）
５ｘ＋２ｙ＝11　…①
ｘ＋２ｙ＝15　…②

①－②をすると、４ｘ＝－４
ｘ＝－１
②に代入、－１＋２ｙ＝15
２ｙ＝16
ｙ＝８
ｘ＝－１、ｙ＝８

（５）
全体は、６×６＝36通り
積が６→１×６、２×３、３×２、６×１の４通り。
確率は４/36＝１/９

（６）

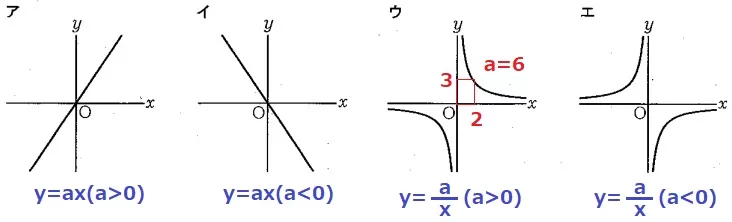
ア・イは比例、ウ・エは反比例。
ａ＞０なのでウ。

（７）
ｘ²－９ｘ＋14
＝（ｘ－２）（ｘ－７）＝０
ｘ＝２、７

（８）
不良品は400個中３個。この割合は母集団5000個も同じ割合とみなす。
不良品の個数は、5000×３/400＝75/２＝37.5≒38個

（９）
ｙ＝ａｘ²に（ｘ、ｙ）＝（－４、５）を代入。
５＝16ａ
ａ＝５/16

（10）①

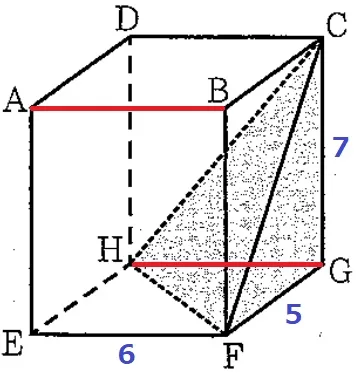
ＡＢと平行な辺はＨＧ。エ
＠＠
他にＡＢと平行なのはＤＣとＥＦ。

②
三角錐Ｃ―ＦＧＨの体積は、５×６÷２×７÷３＝35ｃｍ³

大問３（数量変化）

（１）
最初は90。２枚目以降は105ずつ増加する。
ｘ＝４のとき、90に105を３回たすので、
ｙ＝90＋105×３＝405

ｘ＝７は、90に105を６回足すので、
ｙ＝90＋105×６＝720
ア…405、イ…720

＠別解＠
ｘ＝４→７は３増えるので、405＋105×３＝720と求めてもいい。

（２）
105ずつ増える→変化の割合は105
ｙ＝105ｘ＋ｂに（ｘ、ｙ）＝（１、90）を代入する。
90＝105×１＋ｂ
ｂ＝－15
ｙ＝105ｘ－15

（３）
先の式にｙ＝2085を代入する。
2085＝105ｘ－15
105ｘ＝2100
ｘ＝20

大問４（平面図形）

（１）

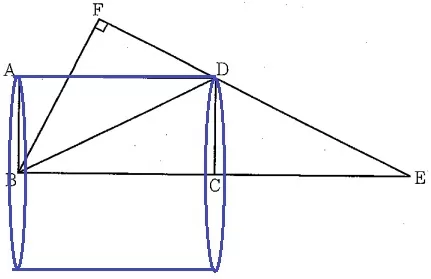
四角形ＡＢＣＤを直線ＢＣを軸として回転させる。
回転体は円柱。ウ

（２）

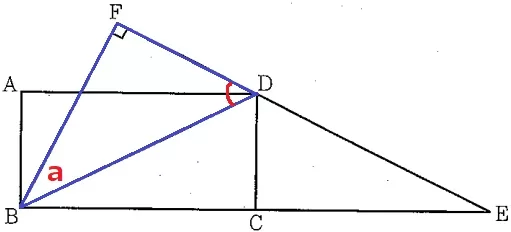
△ＦＢＤの内角から、∠ＢＤＦ＝180－（90＋ａ）＝90－ａ

（３）
△ＦＢＥ∽△ＡＢＤの証明。

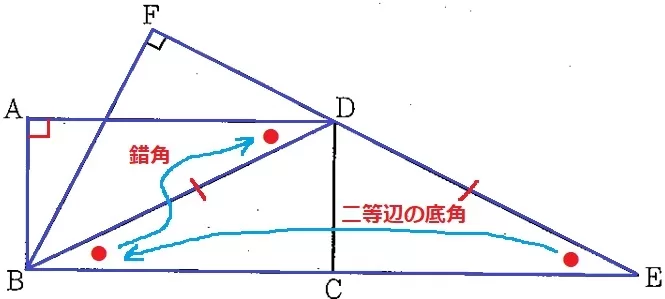
長方形の内角から、∠ＢＡＤ＝90°
∠ＢＦＥ＝∠ＢＡＤ　…①
△ＤＢＥは二等辺三角形なので、∠ＦＥＢ＝∠ＤＢＥ
ＡＤ//ＢＥの錯角で、∠ＡＤＢ＝∠ＤＢＥ
以上より、∠ＦＥＢ＝∠ＡＤＢ　…②
①、②より、２角が等しいから△ＦＢＥ∽△ＡＢＤ
ａ…ＢＡＤ、ｂ…ＡＤＢ、ｃ…ウ

（４）
答案では求め方も説明する。

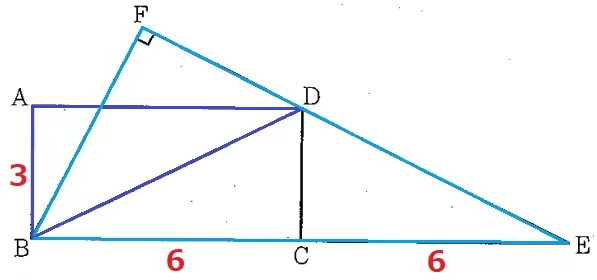
前問の相似が誘導になっている。
求めたいＦＢと対応する辺はＡＢ＝３ｃｍ。
ＢＥ＝12ｃｍと対応するＢＤの長さがわかれば相似比がでる。

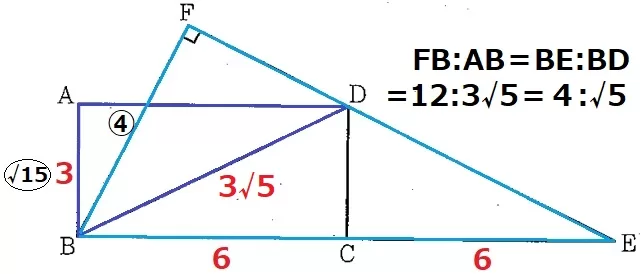
△ＡＢＤで三平方→ＢＤ＝３√５ｃｍ
△ＦＢＥ∽△ＡＢＤより、ＦＢ：ＡＢ＝ＢＥ：ＢＤ
＝12：３√５＝４：√５
ＦＢ＝３×４/√５＝12√５/５ｃｍ