2019年度　長野県公立高校過去問【数学】解説

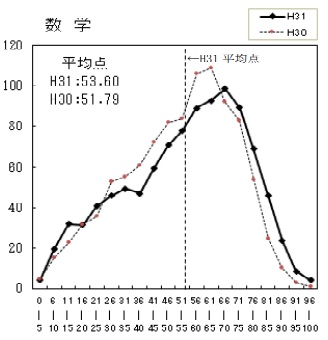
平均53.6点

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①
２－４＝－２

②
２/３×（－６）²
＝２/３×36＝24

③
（√３＋４）（√３－１）
＝３－√３＋４√３－４
＝－１＋３√３

（２）
－２＜－0.05＜１/1000（0.001）＜３
イ

（３）
２つ選ぶ。
３辺の長さ。２辺とあいだの角。
ア・ウ

（４）

孤ＡＤに対する円周角から、∠ＡＢＤ＝∠ＡＣＤ
直径に対する円周角ＡＤＣは90°
ｘ＝180－（90＋68）＝22°

（５）
２ｘ²－２ｘ＝１－５ｘ
２ｘ²＋３ｘ－１＝０
因数分解ができないので、解の公式を適用。
ｘ＝{－３±√３²－４・２・（－１）}/４
＝（－３±√17）/４

（６）
先に式を整理する。
５ｘ－ｙ－２（ｘ－３ｙ）
＝３ｘ＋５ｙ　　←ここで代入
＝３×（－１/３）＋５×３/５
＝－１＋３＝２

（７）
03、12、21、24、30、42（33は×！３は１枚しかない）
全体は、５×４＝20通り
６/20＝３/10

（８）
反比例の比例定数ａ＝ｘｙ
ｘとｙの積はａ（－４）で一定⇒ウ

（９）
70個うち、白：オレンジ＝65：５＝13：１
この割合は母集団も変わらないと推測。
200×13/１＝2600個

（10）
三平方の定理が成り立てば、直角三角形となる。
斜辺であるｃが最も長いので、ａ²＋ｂ²＝ｃ²が成り立つかを調べればよい。

大問２（小問集合２）

（１）①
120人の中央値（メジアン）は、60番目と61番目の平均値。
いずれも５個のところにある。
５

②
お客さんが最も買い求める個数は、最頻値の４個であるから。
*４個入りが最も買われている。

③
方程式の記述問題。
一次方程式であれば、２個買った人をｘ、３個買った人を28－ｘにして、
300ｘ＋450（28－ｘ）＝10950

連立であれば、２個買った人をｘ、３個買った人をｙとおいて、
ｘ＋ｙ＝28…①
300ｘ＋450ｙ＝10950…②

これを解いて、ｘ＝11、ｙ＝17
２個買った人…11人、３個買った人…17人

（２）①
折り鶴の展開図が登場。

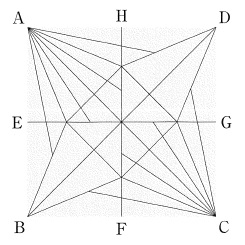
対称の軸を境に左右対称となる。
対象の軸はＢＤ⇒イ
90°回転だと、角が８等分されるマスが左下と右上にきてしまう。
点対称の図形である。⇒エ
イ・エ

②
作図問題。角の２等分線を描く。
点Ｃを示す必要がなく、Ａから伸ばせばいい。
①Ａから適当に弧を描く。
②ＡＢとの交点に針を合わせてシュッ。ＡＤとの交点も同様。
③先の交点を通るようにＡから半直線をひく。

（３）
振り子の周期はおもりの重さや振れ幅ではなく、振り子の長さに依存する。
これを、振り子の等時性といいます。
①
ｙ＝１/４ｘ²に適当な値を放り込む。
ｘ＝２のとき、ｙ＝１
ｘ＝６（２の３倍）のとき、ｙ＝９
１→９なので、９倍。

②
ｙに5.6を代入。
１/４ｘ²＝5.6
ｘ²＝22.4
ｘ＝√22.4
√22.4がどの範囲に属するかを調べる。
√16＜√22.4＜√25だから、
４＜√22.4＜５
よって、４秒以上５秒未満のイ。

大問３（数量変化）

Ⅰ（１）
０～20分までは、毎分３ｃｍ下がるのだから、
５分後には、３×５＝15ｃｍ下がる。

（２）
毎分６ｍｃｍ下がる→傾きは－６
ｙ＝－６ｘ＋ｂにおいて、ｘ＝20、ｙ＝60を代入して切片ｂを求める。
60＝－６×20＋ｂ
ｂ＝180
よって、ｙ＝－６ｘ＋180

（３）①
『ポンプＡとポンプＢが１分間に抜く水の量は同じ』
Ａの故障により、排水の効率は半分に落ちる。
つまり、毎分1.5ｃｍ下がる。
14分後～20分後は６分間なので、1.5×６＝９ｃｍ下がる。
14分後に90ｃｍだったから、90－９＝81ｃｍ

②
もし、昨年のようにＡが壊れていなかった場合、
14分後は、120－３×14＝78ｃｍになっていた。

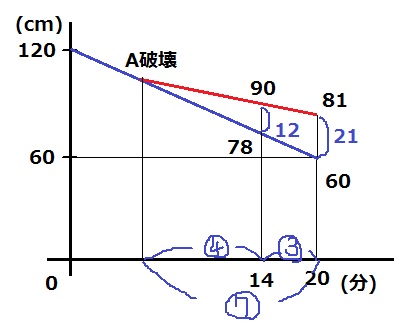
青が昨年、赤が今年。
ここで三角形の相似を利用する。
90－78＝12ｃｍ
91－60＝21ｃｍ
三角形の底辺の比から、12：21＝④：⑦
これを高さ（時間の方）で分配すると、④：③となる。
20－14＝６分が③に相当するから、⑦＝６分×⑦/③＝14分
Ａが壊れたのは、20分の14分前である６分となる。
６分後

③
０～６分後までは昨年と同様。
６分後にＡが破壊。
通常ならば、６分後～20分後の14分間で水面が60ｃｍになる予定であったが、
Ｂだけになったことで排水の効率が半分となり、時間が２倍かかる。
よって、＋14分追加でかかる。

水面の高さが60～30ｃｍの間も、通常ならば20分後～25分後の５分間で完了となるが、
Ｂだけなので時間が２倍かかり、＋５分追加でかかる。
したがって、昨年より19分遅かった。

Ⅱ（１）

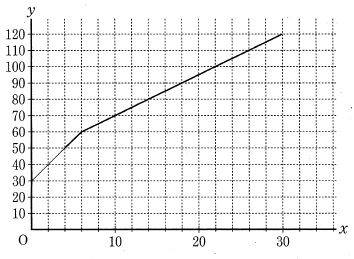
注意点は、水面の高さｙが60ｃｍのときに折れること。
給水量は同じで底面積が２倍になるから、水面の上昇率は半分になる。
60ｃｍ以下は傾き１で、60ｃｍ以上は傾きが１/２（右２上１）。
ｙ＝120までひくと、ｘは30となる。

（２）
ｙ＝100ｃｍのときのｘの値を調べる。
*数値でいえば22分ですね。

大問４（平面図形）

Ⅰ（１）
△ＡＢＤは３：４：５の直角三角形⇒ＢＤ＝10ｃｍ
中点連結定理の形でＢＤの半分がＥＦ。
ＥＦ＝５ｃｍ

（２）

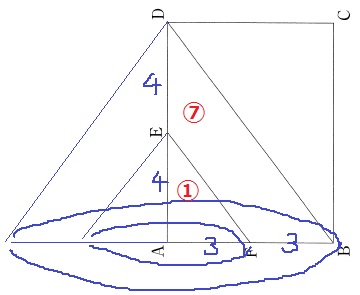
大きい円柱から小さい円柱をひく。
底辺の半径と高さが２倍の関係なので、体積比は①：⑦（全体が２×２×２＝⑧）。
６×６×π×８×１/３×７/８＝84πｃｍ³

Ⅱ
（１）
ウ：ＢＤ//ＦＥから、同位角で∠ＡＢＤ＝∠ＡＦＥ
エ：ＡＢ//ＤＣから、錯角で∠ＡＢＤ＝∠ＢＤＣ

（２）

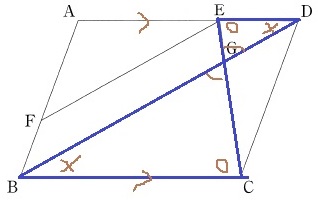
合同の証明問題では基礎レベル。
錯角か対頂角で２角が等しいと指摘。

（３）①
斜線の長さは三平方を用いる。
ＢＤを斜辺とする直角三角形を作成する。

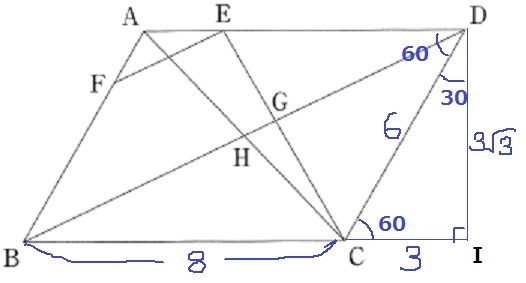
右側に補助線。ＡＤ//ＢＣから錯角で60°を下ろす。
すると、30°－60°－90°の直角三角形が見つかる。
１：２：√３を活用⇒ＣＩ＝３、ＤＩ＝３√３
△ＤＢＩで三平方。
ＢＤ＝√（11²＋３√３²）＝√148＝２√37ｃｍ

②

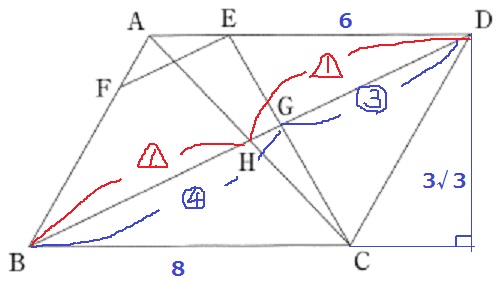
前問で証明した相似を用いる。
△ＧＢＣ∽△ＧＤＥ
ＢＧ：ＧＤ＝８：６＝４：３
平行四辺形の対角線は各々の中点で交わるので、
ＢＨ：ＨＤ＝１：１

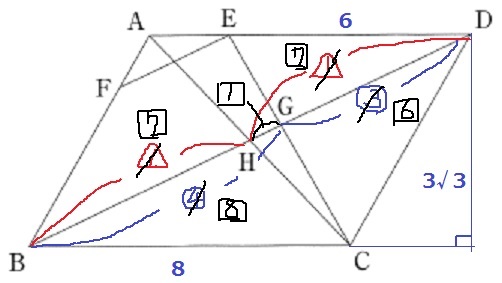
辺ＢＤ上で連比。
ＢＨ：ＨＧ：ＧＤ＝７：１：６
△ＢＣＤは底辺が８、高さが３√３。
△ＣＧＨの面積は、８×３√３×１/２×１/14＝６√３/７ｃｍ²
公立高校入試解説ページに戻る