2024年度　福島県公立高校入試問題過去問【数学】解説

平均23.9点（前年比；＋1.5点）

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）①　98.4％
－５＋９
＝４

②　94.2％
２/５÷（－８/15）
＝－３/４

③　93.3％
７ｘ－３ｙ＋２ｘ＋ｙ
＝９ｘ－２ｙ

④　80.4％（部分正答2.2％）
３√６×√３　←√６＝√３×√２
＝９√２

（２）　66.4％（部分正答0.2％）
（ｘ＋ｙ－１）（ｘ＋ｙ＋１）　←ｘ＋ｙ＝Ａとする
＝（Ａ－１）（Ａ＋１）
＝Ａ²－１　←Ａ＝ｘ＋ｙに戻す
＝（ｘ＋ｙ）²－１
＝ｘ²＋２ｘｙ＋ｙ²－１

大問２（小問集合）

（１）　90.6％
黒ペン…５ａ円、赤ペン…２ｂ円
合計の代金が1020円だから、５ａ＋２ｂ＝1020

（２）　48.5％（部分正答0.5％）
ｙ＝５ｘ＋２の変化の割合は５。
ｘの増加量は４－１＝３、変化の割合＝ｙの増加量÷ｘの増加量だから、
ｙの増加量＝ｘの増加量×変化の割合＝３×５＝15

（３）　58.3％

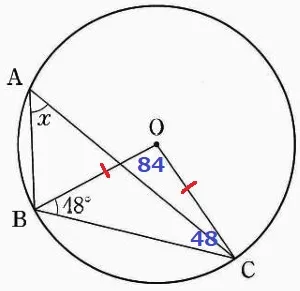
半径から△ＯＢＣは二等辺。
∠ＢＯＣ＝180－48×２＝84°
ｘは弧ＢＣの円周角であり、円周角は中心角の半分だから、
ｘ＝84÷２＝42°

（４）　63.5％
９個の中央値は５番目。
第３四分位数は上位４個の真ん中、上から２番目と３番目の平均値。
118と122の平均である120個。

（５）　62.3％（部分正答1.3％）

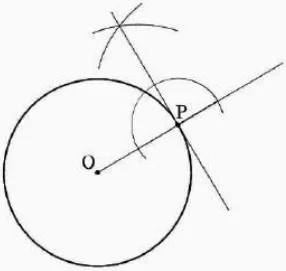
半径と接線は直交する。
点Ｐを通る半直線ＯＰの垂線を作図する。

大問３（確率・整数）

（１）①　66.8％

さいころの出目は１～６、止まる場所も６ヵ所。
Ｐがどこかに止まると、Ｑがそこに止まる出目は１つしかない。
（Ｐ３ならＱ３、Ｐ５ならＱ１）
対応する数がでる確率は１/６。

②　18.1％！

Ａを頂点とする二等辺三角形は上図の４パターン。（正三角形は特別な二等辺三角形）
残り２つの頂点がＰ・Ｑいずれかで４×２＝８通り
全体は６×６＝36通りだから、確率は８/36＝２/９

（２）①　79.5％
タイルの枚数は平方数。
23番目は23²＝529枚

②　19.8％！（部分正答9.7％）
新たに必要なタイルの枚数は、１辺ｎの正方形から１辺ｎ－１の正方形をひけばいい。
ｎ²－（ｎ－１）²
＝ｎ²－ｎ²＋２ｎ－１
＝２ｎ－１
ｎは２以上の整数だから、２ｎ－１は奇数。
よって、新たに必要なタイルの枚数は奇数である。

＠余談＠

連続する奇数の和は平方数である。
７は４番目の奇数→１＋３＋５＋７＝４×４＝16

大問４（方程式）

35.0（部分正答35.0％）
答案では求める過程も記述する。
水を移す前のＡをｘ、Ｂをｙとする。
ｘ＋ｙ＝820　…①

Ａ→Ｃは１/４ｘなので、水を移した後のＡは３/４ｘである。
Ｃの量で等式。
１/４ｘ＋１/３ｙ＝３/４ｘ－60　←両辺12倍して整理
６ｘ－４ｙ＝720　←÷２
３ｘ－２ｙ＝360　…②
①×２＋②をすると、５ｘ＝2000
ｘ＝400
①に代入、ｙ＝820－400＝420
Ａ…400ｍＬ、Ｂ…420ｍＬ

大問５（平面図形）

15.6％！（部分正答20.2％）
ＥＩ＝ＢＩの証明。

ＥＩとＢＩが対応する合同な三角形をみつける。
ＣＩに補助線。
共通辺ＣＩ、合同の長方形（仮定）から、∠ＣＥＩ＝∠ＣＢＩ、ＣＥ＝ＣＢ
斜辺と他の１辺が等しい直角三角形より、△ＣＩＥ≡△ＣＩＢ
対応する辺は等しいから、ＥＩ＝ＢＩ

大問６（関数）

（１）　77.5％
ｙ＝１/４ｘ²にｘ＝－２を代入。
ｙ＝１/４×（－２）²＝１

（２）　57.0％
Ａ（－２、１）→Ｂ（６、９）
右に８、上に８だから、傾きは８/８＝１
Ａから右に２、上に２移動して、切片は１＋２＝３
ｙ＝ｘ＋３

（３）　8.2％!!（部分正答0.7％）

Ｐ（ｔ、１/４ｔ²）Ｑ（ｔ、ｔ＋３）
ＱＰ＝ＰＲよりＱのｙ座標はＰの２倍なので、
１/４ｔ²×２＝１/２ｔ²

Ｑのｙ座標で等式。
１/２ｔ²＝ｔ＋３　←２倍して整理
ｔ²－２ｔ－６＝０
解の公式より、ｔ＝１±√７
０＜ｔ＜６だから、ｔ＝１＋√７
（*√４＜√７＜√９→√７の整数部分は２である）

大問７（空間図形）

（１）　76.2％
△ＤＥＦは辺の比が３：４：５の直角三角形→ＥＦ＝６ｃｍ

（２）①　25.8％！

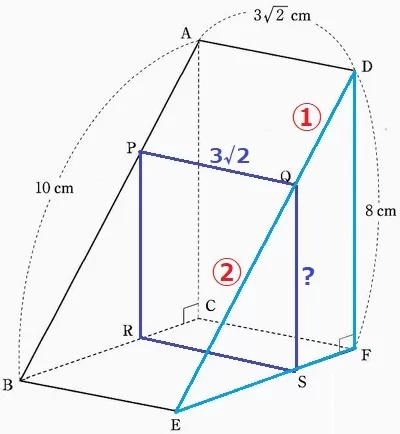
ＰＲ//ＡＣ、ＱＳ//ＤＦ→面ＰＲＳＱと面ＡＣＦＤは平行。
ＰＱ＝ＡＤ＝３√２ｃｍ
△ＱＥＳ∽△ＤＥＦより、ＱＳ＝８×②/③＝16/３ｃｍ
四角形ＰＲＳＱ（長方形）の面積は、３√２×16/３＝16√２ｃｍ²

②　3.4％!!

底面積は四角形ＰＲＳＱ＝16√２ｃｍ²
四角錘Ｔ―ＰＲＳＱの高ささえわかればいい。

（１）よりＥＦ＝６ｃｍでＥＳ：ＳＦ＝２：１だから、ＳＦ＝２ｃｍ
△ＡＣＴ∽△ＳＱＴより、Ｔと面ＰＲＳＱとの距離は２×②/⑤＝４/５ｃｍ
四角錘の体積は、16√２×４/５÷３＝64√２/15ｃｍ³