平均12.1点（前年比；＋2.4点）
問題はコチラ→ＰＤＦファイル
Ａグループの解説はコチラ。
出題範囲の削減はないが、基礎的・基本的な事項をより重視して出題。
大問１（小問集合）
（１）
３－７×（５－８）
＝３－７×（－３）
＝３＋21
＝24
（２）
27ｘ2ｙ÷（－９ｘｙ）×（－３ｘ）
＝９ｘ2
（３）
√48－３√６÷√２
＝４√３－３√３
＝√３
（４）
（ｘ＋１）（ｘ－８）＋５ｘ
＝ｘ2－７ｘ－８＋５ｘ
＝ｘ2－２ｘ－８
＝（ｘ－４）（ｘ＋２）
（５）
（ｘ＋２）2＝７
ｘ＋２＝±√７
ｘ＝－２±√７
（６）
配ったアメ…10ｂ個、余ったアメ…ｃ個
ａ＝10ｂ＋ｃ
（７）
ア：（53＋45＋51＋57＋49＋42＋50＋45）÷８ ←順番を入れ替えて足し算
＝（50＋90＋100＋110＋42）÷８＝392÷８＝49回〇
仮の平均でもＯＫ。49を仮の平均にすると、
＋４－４＋２＋８＋０－７＋１－４＝０
→平均は49回。
イ：８人の中央値（メジアン）は４番目と５番目の平均で49.5回。×
ウ：最頻値（モード）は45回。×
エ：範囲（レンジ）＝最大値－最小値＝57－42＝15回〇
ア・エ
（８）
小×２≦大
（小、大）
（１、２～６）→５通り
（２、４～６）→３通り
（３、６）→１通り
計９通り、確率は９/36＝１/４
（９）
一次関数ｙ＝６ｘ＋５の変化の割合は傾き６で一定。
ｙ＝ａｘ2において、ｘの値がｐ→ｑまで増加するときの変化の割合はａ（ｐ＋ｑ）
ａ（１＋４）＝６
ａ＝６/５
（10）
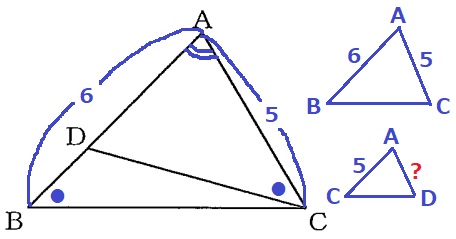
対応する辺がごちゃごちゃになったら、三角形を描いてみよう。
ＡＢ：ＡＣ＝ＡＣ：ＡＤ
ＡＤ＝５×５/６＝25/６ｃｍ
大問２（小問集合２）
（１）
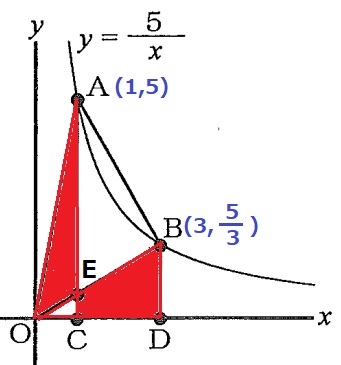
反比例の比例定数ａは積ｘｙで一定である。
△ＡＯＣと△ＢＯＤに注目すると、底辺がｘ座標で高さがｙ座標にあたり、
底辺×高さ÷２の値（面積）が等しい。
面積が等しい△ＡＯＣと△ＢＯＤから共通部分である△ＥＯＣを除くと、
残りの△ＡＯＥと四角形ＥＣＤＢの面積が等しいことになる。
四角形ＥＣＤＢを△ＡＯＥに移す。
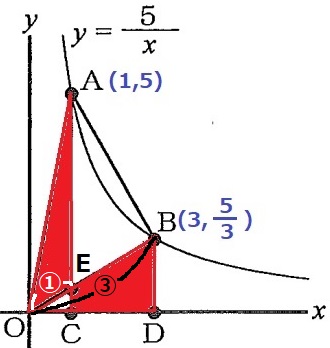
つまるところ、△ＡＯＥ：△ＡＯＢの面積比を求めればいい。
ＥとＢのｘ座標から、△ＡＯＥ：△ＡＯＢ＝ＯＥ：ＯＢ＝１：３
四角形ＥＣＤＢの面積は△ＡＯＢの１/３倍。
（２）
１～２⇒（６＋７＋８＋９）/５＝30/５＝６
２～３⇒（11＋12＋13＋14）/５＝50/５＝10
３～４⇒（16＋17＋18＋19）/５＝70/５＝14
４～５⇒（21＋22＋23＋24）/５＝90/５＝18
【６、10、14、18…】
初項６、公差４の等差数列。
ｎ～ｎ＋１（ｎ番目）⇒６＋４（ｎ－１）＝４ｎ＋２
Ⅰ…10、Ⅱ…14、Ⅲ…18、Ⅳ…４ｎ＋２
（３）①
はじめは25％。
最初の20分は４分あたり＋１％増加するので、20分後は＋５％増加。
１本目の動画の視聴を終えた50分後にちょうど０％になる。
②
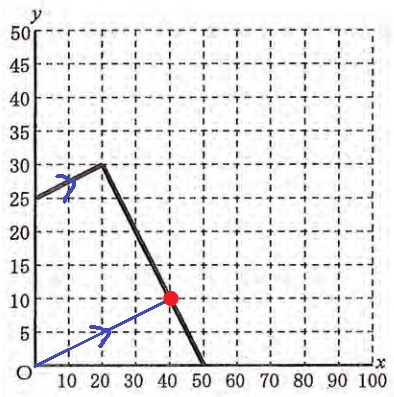
前問のグラフを活用する。
０分０％から始まり、50分０％で終わるので、
Ｏから充電中の傾きに平行な線をひくと交点は40分となる。
40分以上充電すれば、２本目の動画を視聴しきれる。
＠余談＠
バッテリー（リチウムイオン電池）は、充電しながら利用すると劣化が早まるので注意です。
大問３（図形）
（１）
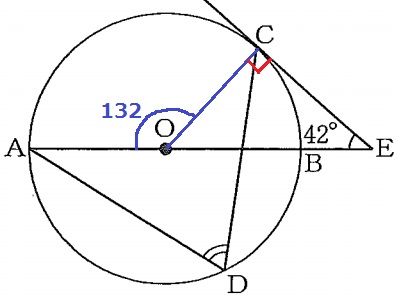
接線があるので、これを使うと予想する。
ＯＣに補助線。半径と接線は垂直ゆえ、∠ＯＣＥ＝90°
△ＯＣＥで外角定理→∠ＡＯＣ＝90＋42＝132°
弧ＡＣに対する円周角が∠ＣＤＡだから、132÷２＝66°
（２）①
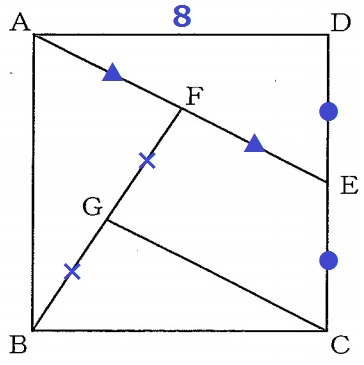
なんとなくＡＥとＧＣが平行っぽい。
だが、●＋×＝90°で角度を調査しても、錯角や同位角が等しいと指摘しにくい。
多くの中点が与えられているので、中点連結定理を適用してＡＥ//ＧＣがいえないか。
ＡＥとＢＣを延長、交点をＨとする。
△ＡＤＥと△ＨＣＥはＤＥ＝ＣＥ、直角と対頂角で１辺と両端角が等しく合同。
ＣＨ＝８ｃｍ
△ＢＣＧと△ＢＨＦに着目する。
ＧはＢＦの中点で、ＣもＢＨの中点。
中点連結定理からＧＣ//ＦＨとなり、やはり平行であった。
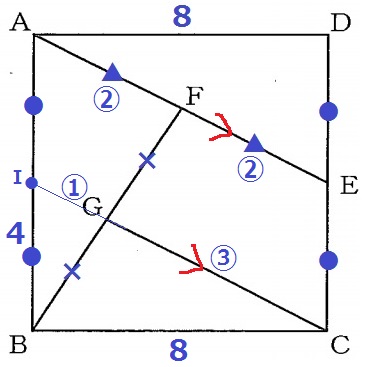
ＣＧを延長、ＡＢとの交点をＩとする。
四角形ＡＩＣＥは２組の対辺が平行だから平行四辺形。
対辺は等しいので、ＡＩ＝ＥＣ（●）
最も短いＩＧ＝①とおく。
△ＩＢＧと△ＡＢＦの中点連結定理でＡＦ＝②
ＦＥ＝②
平行四辺形の対辺から、ＩＣ＝ＡＥ＝④
ＧＣ＝④－①＝③
△ＩＢＣで三平方→ＩＣ＝４√５ｃｍ
ＧＣ＝４√５×③/④＝３√５ｃｍ
②
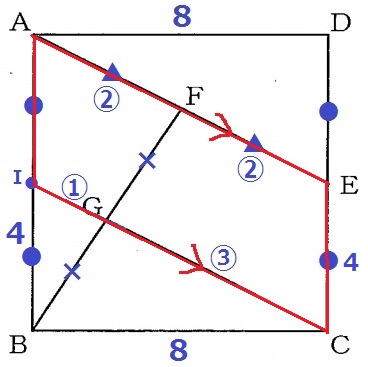
平行四辺形ＡＩＣＥは、４×８＝32ｃｍ2
あとは上底と下底の比の合計で対処する。
平行四辺形ＡＩＣＥの上底ＡＥ＋下底ＩＣ＝④＋④＝⑧
四角形ＦＧＣＥの上底ＦＥ＋下底ＧＣ＝②＋③＝⑤
32×⑤/⑧＝20ｃｍ2
（３）①
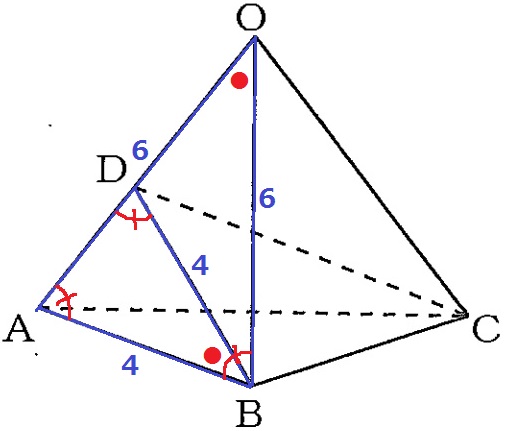
△ＯＡＢは等辺が６ｃｍの二等辺三角形。
△ＢＡＤは等辺が４ｃｍの二等辺三角形。
底角の片方が共通角なので、２つの底角が等しいとわかる。
２角が等しく、△ＯＡＢ∽△ＢＡＤ
ＯＡ：ＡＢ＝ＢＡ：ＡＤ＝３：２
ＡＤ＝４×２/３＝８/３ｃｍ
②
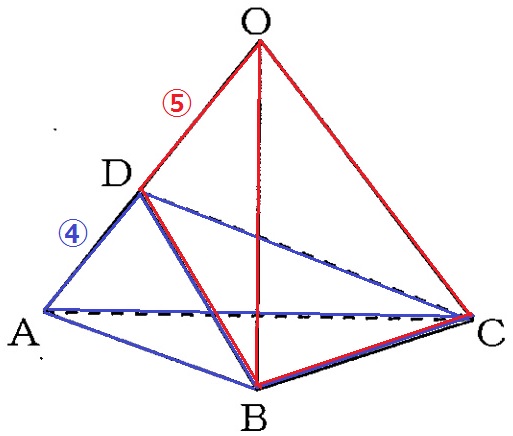
ＯＤ＝６－８/３＝10/３ｃｍ
ＯＤ：ＤＡ＝10/３：８/３＝５：４
三角錐Ａ－ＢＣＤと三角錘Ｏ－ＢＣＤは底面が△ＢＣＤで共通。
高さの比はＡＤ：ＯＤで、これが体積比に相当する。
三角錘Ａ－ＢＣＤ：三角錘Ｏ－ＢＣＤ＝④：⑤
したがって、三角錘Ｏ－ＢＣＤの体積は三角錘Ｏ－ＡＢＣ（全体）の５/９倍。
大問１
（３）ルート同士は約分できる。
（５）カッコを展開しない方がスムーズ。
大問２
（１）反比例は積ｘｙが一定⇒横×縦が一定⇒三角形の底辺×高さが一定
⇒△ＡＯＣと△ＢＯＤの面積は等しく、四角形ＥＣＤＢを△ＡＯＥに移転できる。
ＯＥ：ＯＢさえわかればいい。
（２）分子の合計は20ずつ増える。
（３）②グラフの活用でサッと求められるユニークな問いであった。
大問３
（２）平行の根拠が見えにくい。
外側に合同図形をつくる。中点連結定理で平行さえつかめれば正解にグッと近づく。
いろいろな攻め方があるが、解説では②を念頭に辺の比を先に調べた。
（３）②上と下の立体は△ＢＣＤでピッタリくっついている。
ここから△ＢＣＤを底面としたときの高さの比に着目する。
公立高校入試解説ページに戻る
コメント