2021年度　早稲田中学過去問【算数】大問４解説

問題ＰＤＦ
図１のような直方体があります。点Ｐは直方体の辺上を点Ａを出発して、
一定の速さでＡ→Ｂ→Ｃ→Ｄの順に動き、その後1.5倍の速さでＤ→Ｅ→Ｆ→Ａの順に動きました。
図２は、点Ｐが点Ａを出発してからの時間と三角形ＡＤＰの面積との関係を表したグラフです。
次の問いに答えなさい。

（１）
点ＰはＡ→Ｂ→Ｃ→Ｄを毎秒何ｃｍの速さで動きますか。

（２）
三角形ＡＤＰが４回目に二等辺三角形になるのは、点Ａを出発してから何秒後ですか。

（３）
直方体の体積は何ｃｍ³ですか。

＠解説＠
（１）

ＰがＡＢＣＤ上を移動しているとき、最初の５秒がＡＢ、最後の５秒がＣＤ、
あいだの６秒がＢＣとなる。
長さがわからないので、ＡＢ＝⑤、ＢＣ＝⑥とすると、
⑤×⑥÷２＝60
⑤×⑥＝120
⑤と⑥の倍数で調査。
２倍して、10×12＝120　←ＯＫ！
ＡＢ＝10ｃｍをＰは５秒で移動するから毎秒２ｃｍ。

（２）
ＢＣ（⑥）＝12ｃｍ
直方体の高さが気になる。

グラフの後半部分。
直方体の高さであるＤＥはわからないが、ＥＦ＝ＢＣ＝12ｃｍ。
先ほどＢＣ間が６秒だったので、1.5倍速では６×２/３＝４秒かかる。
ＤＥ（ＦＡ）間は（20－４）÷２＝８秒
Ｐは毎秒３ｃｍ動くので、ＤＥ＝３×８＝24ｃｍ

４回目に二等辺となるＰの位置を調査。

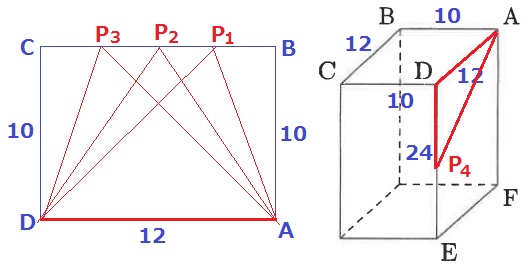
おそらく、１回目と３回目が飛ばされやすいかと思われる。
等辺が12ｃｍになるとき、Ｐは中途半端な場所にある。
４回目に二等辺となるのは、ＰがＤＥの中点にあるとき。
Ｐは16秒後にＤに着くので、16＋12÷３＝20秒後

（３）
10×12×24＝2880ｃｍ³
難関中（算数科）解説ページに戻る